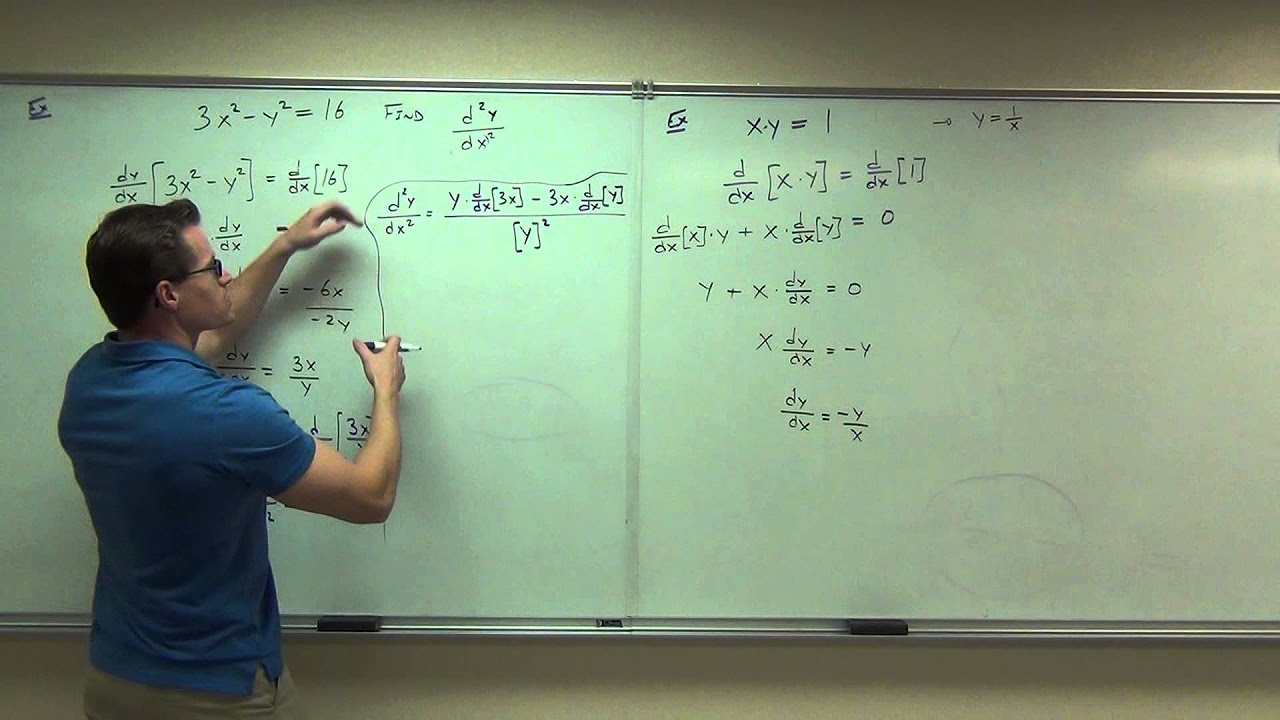Calculus AB Lesson 4.1: Implicit Differentiation
TLDRThis educational video script delves into the concept of implicit differentiation, offering clear examples to illustrate the process. It explains how to differentiate equations not in explicit form, emphasizing the chain rule's importance when the variable of differentiation isn't the independent variable. The script guides viewers through finding derivatives of various functions, including those with multiple variables, and demonstrates how to solve for specific points on a curve, such as horizontal and vertical tangents. It also covers the calculation of second derivatives and concludes with finding tangent lines at given points, providing a comprehensive understanding of implicit differentiation.
Takeaways
- 📚 Implicit differentiation is a method used to find the derivative of a function when it is not explicitly defined in terms of the independent variable.
- 🔍 The derivative, denoted as dy/dx, represents the rate of change of the dependent variable y with respect to the independent variable x.
- 📈 The power rule is applied to find derivatives of terms like y = x^n, resulting in dy/dx = n * x^(n-1).
- 📉 The slope of a curve at a point is the rise over run, which is analogous to the derivative dy/dx, representing the change in y per unit change in x.
- 👆 When the derivative is a positive number, it indicates that y increases as x increases; a negative number indicates the opposite.
- 🔄 The chain rule is essential for finding derivatives when the function is not in terms of the independent variable x, requiring multiplication by (dy/dx) or (dx/dy) as appropriate.
- 🔢 The process of implicit differentiation involves differentiating both sides of an equation with respect to x, considering all variables as functions of x.
- ⚖️ When solving for dy/dx in implicit differentiation, terms with dy/dx are isolated on one side of the equation, and terms without are moved to the other side.
- 📐 The concept of explicit and implicit equations is introduced, with explicit equations having one variable isolated on one side, and implicit equations not having this form.
- 🤔 Solving for a horizontal tangent involves setting the derivative equal to zero and solving for the variables, as a horizontal tangent has a slope of zero.
- 📉 To find where a curve has a vertical tangent, look for where the derivative is undefined, typically where the denominator of the derivative expression equals zero.
Q & A
What is the main topic of the video?
-The main topic of the video is implicit differentiation, including examples and methods to find the derivative of functions without explicitly solving for one variable.
What is the derivative of y with respect to x in the equation y = x^3?
-The derivative of y with respect to x in the equation y = x^3 is 3x^2, using the power rule for differentiation.
What does dy/dx represent in the context of the video?
-In the context of the video, dy/dx represents the slope of the tangent line to the curve of a function at a particular point, which is the rate of change of y with respect to x.
How does the video explain the concept of slope in the context of derivatives?
-The video explains the concept of slope as the change in y over the change in x (Δy/Δx), which can be interpreted as the change in the dependent variable per unit increase in the independent variable.
What is the difference between explicit and implicit equations in the video?
-Explicit equations have one variable isolated on one side of the equation, while implicit equations do not have variables explicitly isolated and often involve multiple variables on both sides.
How does the video demonstrate the process of implicit differentiation?
-The video demonstrates implicit differentiation by taking the derivative of each term in an equation with respect to x, using the chain rule when necessary, and then solving the resulting equation for dy/dx.
What is the purpose of using implicit differentiation for equations that can be solved explicitly?
-The purpose of using implicit differentiation for equations that can be solved explicitly is to find the derivative without the need to rearrange the equation into an explicit form, which can be more efficient in certain cases.
How does the video handle the derivative of an equation with a variable that is not the independent variable?
-The video handles this by using the chain rule to adjust the derivative to be in terms of the independent variable, multiplying by the derivative of the independent variable with respect to the actual variable used.
What is the significance of finding the second derivative in the context of the video?
-The significance of finding the second derivative in the context of the video is to determine the concavity of a function or to find points of inflection, which can provide additional information about the function's behavior.
How does the video illustrate the concept of horizontal and vertical tangents?
-The video illustrates the concept of horizontal tangents by finding where the derivative (slope) is zero and vertical tangents by finding where the derivative is undefined, often due to division by zero in the derivative equation.
What is the method used in the video to find the equation of a tangent line at a given point?
-The method used in the video to find the equation of a tangent line at a given point involves finding the derivative at that point to get the slope, using the point-slope form of a line, and then substituting the point and solving for the equation of the line.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, starting with basic examples such as finding the derivative of y with respect to x in the equation y = x^2. The explanation covers the power rule and the interpretation of dy/dx as the slope of the tangent line to the curve at any given point. It emphasizes the meaning of slope as the change in y over the change in x, and provides a clear example to illustrate this concept.
🔍 Understanding Slope and Variable Change
The second paragraph delves deeper into the concept of slope, explaining how it represents the change in the dependent variable per unit increase in the independent variable. It discusses the difference between dy/dx and dy/dt, highlighting the importance of matching the derivative with the correct variable. The paragraph also introduces the method of multiplying by dt/dx to convert a derivative with respect to one variable into another, using the chain rule to adjust for the change in variables.
📘 Applying Chain Rule in Differentiation
This paragraph focuses on the application of the chain rule in implicit differentiation, providing several examples. It explains how to find the derivative of expressions like Y^3 with respect to X when Y is not explicitly in terms of X, and how to adjust derivatives from one variable to another using the chain rule. The examples include taking derivatives of W^4, 6z, x^2 + y, and x^2 + y^2 with respect to X, showcasing different scenarios where the chain rule is necessary.
📐 Differentiating Explicit and Implicit Equations
The fourth paragraph discusses the difference between explicit and implicit equations, explaining that explicit equations have one variable isolated on one side, which makes them easier to graph and differentiate. It contrasts this with implicit equations, which do not have variables isolated and thus require implicit differentiation. The paragraph provides examples of both types of equations and demonstrates how to differentiate them, including converting an implicit equation into an explicit one if possible.
📉 Implicit Differentiation and Tangent Slope
This paragraph explains how to use implicit differentiation to find the slope of the tangent line to a curve at a specific point. It provides an example of differentiating the equation x^2 + y^2 = 25 to find dy/dx, and then solving for dy/dx explicitly. The explanation includes the steps to adjust the derivative equation to isolate dy/dx, resulting in a slope that can be evaluated at any point on the curve.
📈 Finding Slopes of Tangent Lines at Specific Points
The sixth paragraph continues the discussion on implicit differentiation, focusing on finding the slope of the tangent line at a specific point on a curve. It uses the example of the curve defined by x^3 + y^3 = 4xy + 1, and demonstrates the process of differentiating this equation to find dy/dx. The paragraph also explains how to evaluate the derivative at a given point (1, -2) to find the slope of the tangent line at that point.
🌟 Identifying Horizontal and Vertical Tangents
This paragraph discusses how to determine where a curve has horizontal or vertical tangents by analyzing the derivative. It explains that a horizontal tangent corresponds to a slope of zero, which occurs when the numerator of the derivative fraction is zero, while a vertical tangent corresponds to an undefined slope, which occurs when the denominator of the derivative fraction is zero. The paragraph provides a method to solve for these points using a system of equations derived from the original curve equation and the condition for horizontal or vertical tangents.
🔢 Solving for Tangent Lines and Points of Interest
The seventh paragraph further explores the process of finding horizontal and vertical tangents by solving a system of equations. It demonstrates how to use substitution to find the x-values where the curve has vertical tangents and how to use the original curve equation to find the corresponding y-values. The paragraph also explains how to identify points of interest on the curve, such as where the tangent is horizontal or vertical.
📝 Calculating Second Derivatives and Analyzing Curve Behavior
This paragraph introduces the concept of second derivatives, explaining how to calculate them using Leibnitz notation and the quotient rule. It provides examples of finding second derivatives for given equations and discusses the significance of second derivatives in analyzing the concavity and inflection points of a curve.
🔍 Further Exploration of Second Derivatives and Tangent Lines
The eighth paragraph continues the exploration of second derivatives with additional examples, showing how to find them for different equations. It also discusses how to write equations for horizontal tangent lines to a curve by setting the first derivative to zero and solving for the variables. The paragraph demonstrates the process of finding specific points on the curve where horizontal tangents exist.
📌 Finding Points of Tangency and Their Slopes
The ninth paragraph concludes the script by discussing how to find the points of tangency and their slopes for a given curve. It provides a method to determine the x and y coordinates of a point where a line with a specific slope is tangent to the curve. The paragraph also explains how to use the first derivative to find the slope of the curve at a given point and how to use this information to write the equation of the tangent line.
📐 Implicit Differentiation and Tangent Line Equations
The final paragraph summarizes the process of using implicit differentiation to find the equation of the tangent line at a given point on a curve. It provides specific examples, including finding the slope of the curve at a particular point and using this information to write the equation of the tangent line. The paragraph also touches on the derivative of trigonometric functions and how to apply implicit differentiation in various scenarios.
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Power Rule
💡Chain Rule
💡Tangent Line
💡Independent Variable
💡Dependent Variable
💡Product Rule
💡Quotient Rule
💡Horizontal Tangent
Highlights
Introduction to implicit differentiation with examples.
Explanation of 'dy/dx' as the rate of change of Y with respect to X.
Power rule application in finding derivatives.
Interpretation of the slope in the context of a graph.
Differentiation between dependent and independent variables in differentiation.
Use of chain rule to adjust derivatives when the variable is not with respect to X.
Illustration of how to find dy/dx when the equation involves a different variable (T).
Practice with various examples to solidify understanding of implicit differentiation.
Explanation of explicit and implicit equations and their importance in differentiation.
Technique to convert an implicit equation to an explicit form if possible.
Method to find the derivative of an equation without explicit form using implicit differentiation.
Solving for dy/dx in implicit form by isolating the term.
Finding the slope of the tangent line at a specific point on a curve.
Identifying horizontal tangents by setting the derivative equal to zero.
Solving a system of equations to find specific points on a curve.
Determining vertical tangents by finding where the derivative is undefined.
Second derivative calculation using implicit differentiation.
Application of implicit differentiation to find the equation of a tangent line at a given point.
Using implicit differentiation to find dy/dx for a complex equation involving trigonometric functions.
Conclusion summarizing the process and applications of implicit differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: