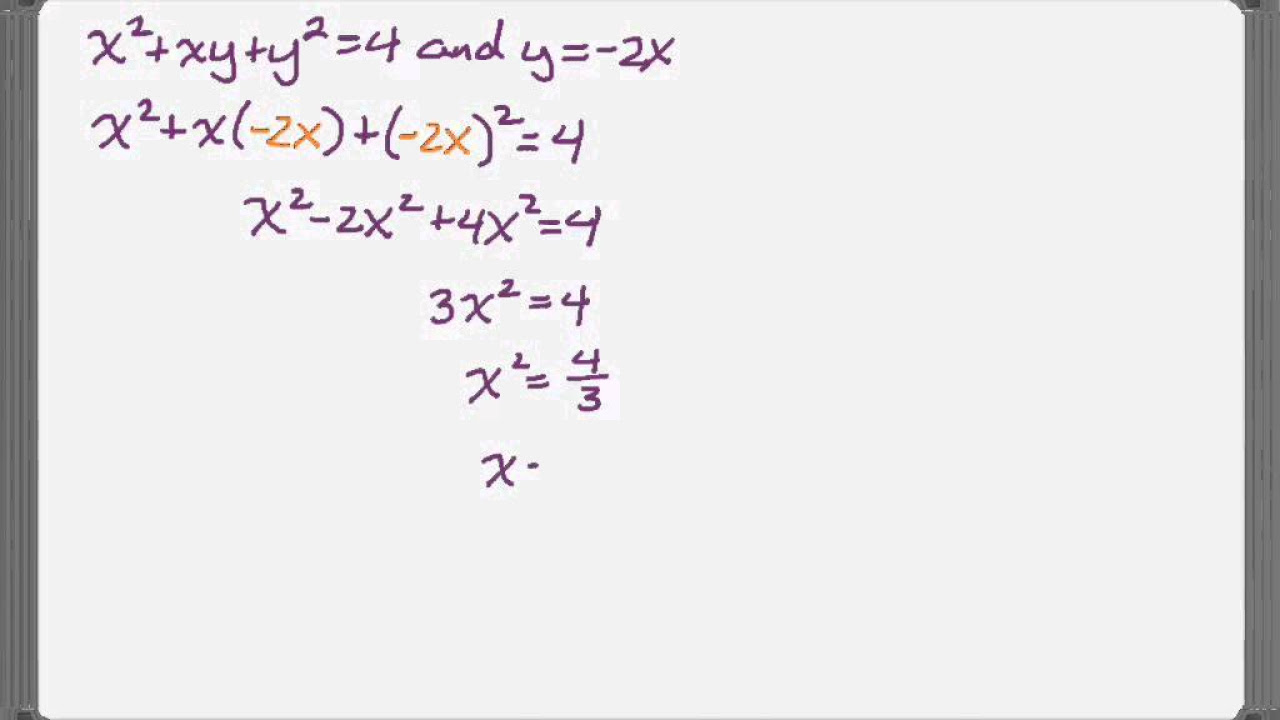Math1325 Lecture 11 3 - Implicit Differentiation
TLDRThis transcript from a Math 1325 lecture introduces the concept of implicit differentiation, a method for finding derivatives of functions that are not explicitly defined in terms of \( y \) with respect to \( x \). The lecture explains that while explicit functions have \( y \) isolated on one side of the equation, implicit functions have \( y \) intermixed with \( x \). The process involves differentiating both sides of the equation with respect to \( x \), applying the chain rule, and solving for \( \frac{dy}{dx} \) or \( y' \). Several examples are provided to illustrate the technique, including finding the slope of tangents at specific points and determining where horizontal and vertical tangents occur. The lecture emphasizes the importance of practice, encouraging students to work through recommended problems on WebAssign for further understanding.
Takeaways
- 📖 Implicit differentiation is used to find the derivatives of functions that are not explicitly defined in terms of y with respect to x.
- 🔑 The process involves differentiating both sides of an equation with respect to x, using the chain rule when differentiating terms involving y.
- 🔯 When differentiating with respect to x, terms involving y are treated as a product of y and its derivative with respect to x, denoted as y' or dy/dx.
- 📈 The derivative of y with respect to x gives the slope of the tangent line to the curve represented by the function at any point.
- 🟑 To find the slope at a specific point, substitute the coordinates of that point into the derived expression for y'.
- 🗲 For equations with multiple y terms, solve algebraically for y' to simplify the expression for the slope.
- 🔍 To find the equation of a tangent line, use the point-slope form y - y1 = m(x - x1), where m is the slope and (x1, y1) is the point of tangency.
- 🐬 Horizontal tangent lines occur where the slope of the function is zero, which can be found by setting the derived y' expression equal to zero and solving for x.
- 🚫 Vertical tangent lines occur where the slope is undefined, which happens when the denominator in the expression for y' is zero.
- 📐 The process of implicit differentiation can handle more complex functions, including those involving products and higher powers, by applying the product rule and chain rule as needed.
- 📒 It is recommended to practice implicit differentiation with a variety of problems, as suggested in the course syllabus and electronic text on WebAssign.
Q & A
What is an explicit function?
-An explicit function is a function where the variable y is isolated on one side of the equation, and everything else is on the other side with only x's in it. It can be easily defined in terms of x alone, allowing you to calculate the value of y directly from x.
How is the derivative of an explicit function found?
-The derivative of an explicit function is found by taking the derivative with respect to x only, using the notation d/dx. This involves applying the rules of differentiation to the terms involving x.
What is an implicit function?
-An implicit function is a function where y is not isolated on one side of the equation, and the relationship between x and y is not explicitly defined. Changes in x will affect y, but the function does not have y solely on one side of the equation.
How is the derivative of an implicit function found?
-The derivative of an implicit function is found using a method called implicit differentiation. This involves taking the derivative of both sides of the equation with respect to x, applying the chain rule when necessary, and solving for dy/dx or y'.
What is the chain rule in the context of differentiation?
-The chain rule is a fundamental principle used in calculus to find the derivative of a function composed of two or more functions. When differentiating an expression like y(x), where y is a function of x, you multiply the derivative of the outer function (dy/dy) by the derivative of the inner function (dx/dx).
How do you differentiate an equation with a constant term?
-The derivative of a constant term is zero. When differentiating an equation with a constant term with respect to x, you simply apply the rule that the derivative of a constant is zero and do not include it in the resulting derivative expression.
What does the derivative of a function represent?
-The derivative of a function represents the slope of the tangent to the graph of the function at a particular point. It gives the rate of change of the function at that point.
How do you find the slope of the tangent line at a specific point on a curve?
-To find the slope of the tangent line at a specific point, you first find the derivative of the function, which gives the slope of the tangent line. Then, you substitute the x and y values of the specific point into the derivative to find the slope at that point.
What is the product rule in differentiation?
-The product rule is a formula used in calculus to find the derivative of a product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How do you find the equation of a tangent line using the point-slope form?
-To find the equation of a tangent line using the point-slope form, you first determine the slope of the tangent line at the given point by differentiating the function. Then, you use the point-slope form of a line, which is y - y1 = m(x - x1), where m is the slope and (x1, y1) is the point on the line.
What is a horizontal tangent and how do you find its points on a curve?
-A horizontal tangent is a tangent line that has a slope of zero. To find the points on a curve with a horizontal tangent, you set the derivative of the function equal to zero and solve for the variable, which will give you the x and y coordinates of the points where the tangent is horizontal.
What is a vertical tangent and how do you find its points on a curve?
-A vertical tangent is a tangent line that has an undefined slope. To find the points on a curve with a vertical tangent, you find when the derivative of the function is undefined, which typically happens when the denominator of a fraction is zero. You then solve for the variable to find the x and y coordinates of the points where the tangent is vertical.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, contrasting it with explicit functions. It explains that while explicit functions have y directly calculated from x, implicit functions have y related to x without being isolated on one side of the equation. The paragraph uses the example of an equation relating x and y, which cannot be easily solved for y, to illustrate the need for implicit differentiation. It then demonstrates the process of differentiating an equation implicitly, applying algebraic techniques and the chain rule to find the derivative of y with respect to x, symbolized as y prime.
🔍 Derivatives of Implicit Functions
The second paragraph delves into the process of finding derivatives of implicit functions. It emphasizes the use of the chain rule and the importance of differentiating with respect to y and then multiplying by dy/dx when dealing with y terms. The paragraph provides examples of how to algebraically manipulate equations to solve for y prime, showing how to handle equations with multiple y terms. It also demonstrates how to find the slope of the tangent at specific points on a graph by substituting values into the derived formula.
🔢 Solving for Tangent Lines and Special Tangents
The final paragraph discusses solving for the equations of tangent lines to a curve at specific points, including when the tangent is horizontal or vertical. It explains how to find when the derivative is zero (indicating a horizontal tangent) or undefined (indicating a vertical tangent) by setting the numerator or denominator of the derivative to zero, respectively. The paragraph provides a step-by-step method for solving these cases, including factoring and applying the quadratic formula. It concludes with a reminder to practice the concepts through homework and sample problems, recommending the use of WebAssign for additional practice.
Mindmap
Keywords
💡Implicit Differentiation
💡Explicit Function
💡Chain Rule
💡Derivative
💡Slope of the Tangent
💡Quadratic Equation
💡Product Rule
💡Horizontal Tangent
💡Vertical Tangent
💡Rational Expression
💡Ellipse
Highlights
Introduction to implicit differentiation as a method to find derivatives of functions that are not explicitly defined in terms of x alone.
Explanation of explicit functions where y can be isolated on one side of the equation.
Differentiating y with respect to x using the chain rule when y is an implicit function of x.
Example of differentiating the equation of a line from slope-intercept form to standard form.
Use of algebraic techniques to manipulate the differentiated equation and solve for dy/dx.
Deriving the slope of the tangent to the graph of y^2 = x at specific points x=2 and x=-2.
Differentiating more complex functions, such as x^2 + y^2 - 9 = 0, to find the slope of the tangent at a given point.
Application of the product rule in implicit differentiation when dealing with terms involving both x and y.
Writing the equation of the tangent line using the point-slope form after finding the slope.
Identifying conditions for a horizontal tangent (slope of zero) and a vertical tangent (undefined slope).
Solving for x and y values where the derivative is zero to find points with horizontal tangents.
Finding points where the derivative is undefined by setting the denominator of the derivative to zero for vertical tangents.
Visualizing the function as an ellipse and identifying the points of horizontal and vertical tangents.
Recommendation to practice implicit differentiation with provided sample problems in the electronic text on WebAssign.
Emphasis on the importance of doing homework and attempting recommended problems for better understanding.
Explanation of the process of differentiating with respect to x and then isolating dy/dx using algebraic manipulation.
Illustration of how to handle constant terms in differentiation, noting that the derivatives of constants are zero.
Use of the quotient rule and factoring techniques to simplify the derivative and solve for dy/dx.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: