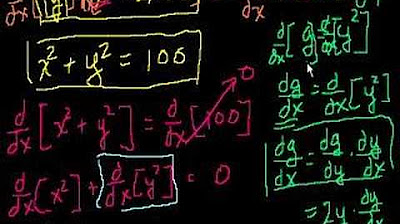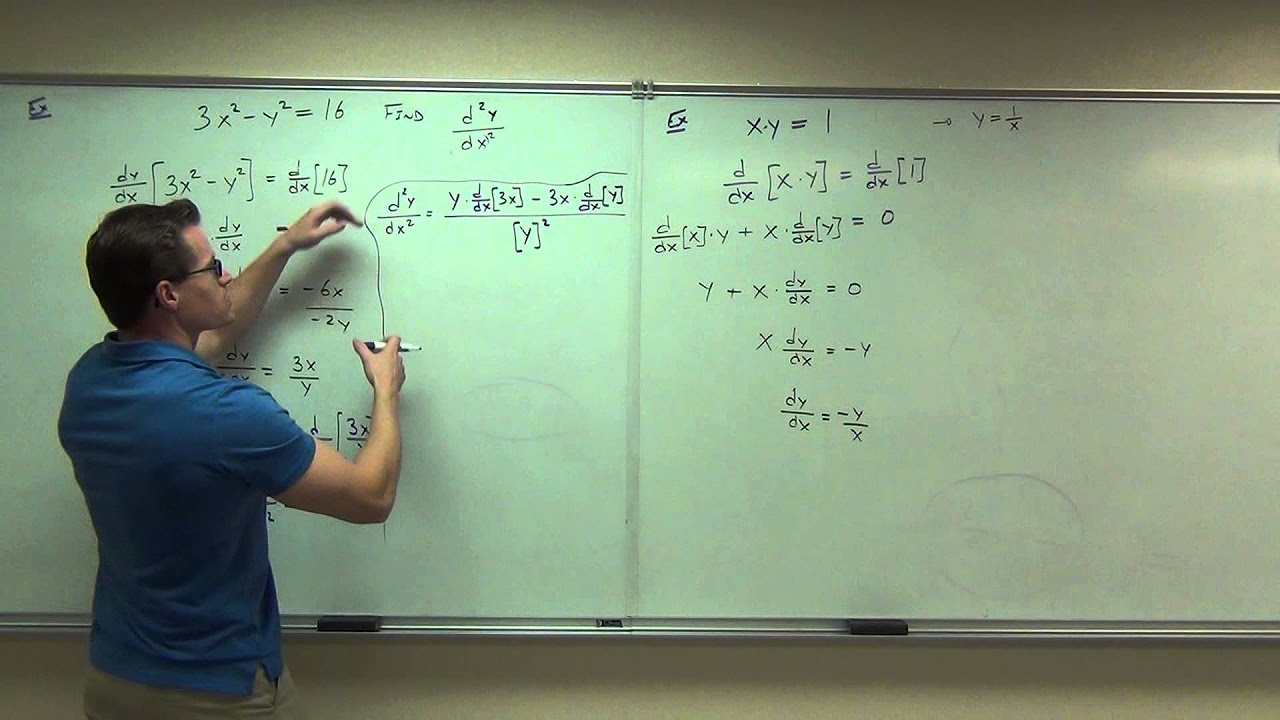Introduction to Implicit Differentiation
TLDRThis video introduces the concept of implicit differentiation, contrasting it with explicit functions. The presenter explains that in explicit functions, the dependent variable y is clearly isolated, whereas in implicit functions, y and x are intermixed. The video demonstrates how to find derivatives of implicit functions using examples, such as ( y = x^2 + 3 ) raised to the fourth power, and ( y^5 ). The key takeaway is that when differentiating y, one must multiply by y' (the derivative of y with respect to x). The video also shows how to apply the product rule and chain rule in implicit differentiation, and concludes by illustrating that implicit differentiation can yield the same results as explicit differentiation, even when an explicit form is possible.
Takeaways
- 📌 The difference between explicit and implicit functions lies in the clarity of the independent variable (x) and dependent variable (y). Explicit functions clearly state y as a function of x, while implicit functions do not isolate y on one side.
- 📝 To differentiate an explicit function, you can directly apply differentiation rules. For example, the derivative of y = x^2 + 2x is y' = 2x + 2.
- 🔍 Implicit differentiation is necessary when y is not isolated and mixed with x in the function. It involves differentiating both x and y terms and applying the chain rule.
- 📐 The power rule and chain rule are essential in implicit differentiation, as seen in the example of differentiating x^2 + 3 raised to the fourth power.
- 🔑 A key rule in implicit differentiation is that every time you differentiate y (the dependent variable), you multiply by y' (the derivative of y with respect to x).
- 🧩 When using implicit differentiation, you often end up with an equation that includes both x's and y's, and you need to solve for y' (the derivative of y).
- 🌐 In the case of an equation that can be both explicit and implicit, both methods will yield the same derivative, but implicit differentiation is more versatile when y is not explicitly defined.
- ✅ To solve for y' in an implicit differentiation problem, you often need to rearrange the terms and factor out y' to isolate it on one side of the equation.
- 🤔 The product rule is also used in implicit differentiation when the function involves a product of two expressions, one involving x and the other y.
- 📉 Implicit differentiation can handle complex functions where y is not explicitly defined in terms of x, which would be difficult or impossible to differentiate using explicit methods.
- 🔗 The final answer in implicit differentiation is often expressed in terms of both x and y, which is acceptable as it represents the derivative of y with respect to x.
Q & A
What is the main difference between an explicit and an implicit function?
-An explicit function clearly states the dependent variable (usually y) as a function of the independent variable (x), with y isolated on one side of the equation. An implicit function, on the other hand, does not isolate y; instead, the variables x and y are intermixed, implying that y is a function of x without explicitly stating it.
How does one find the derivative of an explicit function, such as y = x^2 + 2x?
-To find the derivative of an explicit function, you apply standard differentiation rules. For y = x^2 + 2x, the derivative (y') is found by differentiating each term separately: the derivative of x^2 is 2x, and the derivative of 2x is 2, so y' = 2x + 2.
What is the process for differentiating an implicit function?
-To differentiate an implicit function, you apply the chain rule and power rule as needed. You treat y as a function of x and differentiate both sides of the equation with respect to x. Whenever you differentiate an occurrence of y, you multiply by y' (the derivative of y with respect to x).
How do you solve for y' when you have differentiated an implicit function?
-After differentiating, you'll usually have an equation with y' as part of the terms. To solve for y', you'll need to rearrange the equation algebraically to isolate y' on one side. This may involve factoring out y', moving terms around, and simplifying.
What is the 'golden rule' for implicit differentiation?
-The 'golden rule' for implicit differentiation is that every time you take the derivative of y (the dependent variable), you must multiply it by y' (the derivative of y with respect to x).
What is the product rule, and how is it applied in implicit differentiation?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function (f'g + fg'). In implicit differentiation, this rule is used when you have a product of terms involving x and y, and you apply it while also differentiating y terms by multiplying by y'.
Can implicit differentiation always be converted to explicit differentiation?
-No, not always. Implicit differentiation is used when the function cannot be easily or meaningfully written in explicit form. However, if it is possible to express y explicitly in terms of x, then you can convert the implicit differentiation to explicit form for easier differentiation.
What is the role of the chain rule in implicit differentiation?
-The chain rule is essential in implicit differentiation when you have a composite function or when differentiating terms that include y. It allows you to differentiate these terms by applying the derivative of the outer function (multiplied by the derivative of the inner function).
How does the process of implicit differentiation help in finding the derivative of functions that are not easily expressed explicitly?
-Implicit differentiation allows you to find the derivative of a function without explicitly expressing y in terms of x. This is particularly useful for complex functions where separation of variables is not straightforward, as it enables you to find y' directly from the given equation.
What is the final form of the derivative in implicit differentiation?
-The final form of the derivative in implicit differentiation is typically expressed in terms of both x and y, with y' isolated on one side of the equation. This form acknowledges that y is a function of x, and it provides the rate of change of y with respect to x.
Why is it important to isolate y' when solving for the derivative in implicit differentiation?
-Isolating y' is important because it provides the derivative of y with respect to x, which is the primary goal of differentiation. It also makes it easier to interpret the rate of change of y in terms of x and to use the derivative in further calculations or analysis.
Outlines
📚 Introduction to Implicit Differentiation
The video begins with an introduction to the concept of implicit differentiation, contrasting it with explicit functions. It explains that in explicit functions, y is isolated and clearly defined as a function of x, whereas in implicit functions, y and x are intermixed, and the relationship is implied rather than explicitly stated. The video then demonstrates how to find the derivative of an implicit function using the power rule and chain rule, with an example involving x squared plus three raised to the fourth power. It also shows how to handle the derivative when y is explicitly stated as a function of x, highlighting the substitution of y for x squared plus 3 and the resulting derivative.
🧮 Derivatives of Implicit Functions: Power Rule and Chain Rule
This paragraph delves into the process of taking derivatives of implicit functions. It uses the power rule to differentiate y to the fifth, and then applies the chain rule by multiplying by y prime. The paragraph emphasizes the importance of multiplying the derivative of y by y prime whenever y (the dependent variable) is differentiated. It concludes with solving for y prime by factoring out y prime from the equation and isolating it on one side. The approach is illustrated with an example involving e^x multiplied by y cubed, which requires both the product rule and implicit differentiation.
🔍 Solving for y Prime in Implicit Differentiation
The paragraph focuses on solving for y prime in implicit differentiation problems. It presents a method to rearrange terms and isolate y prime on one side of the equation. The process is demonstrated with an example where e^x is multiplied by y cubed, leading to an equation that, after rearrangement and division, yields y prime in terms of x and y. The video also shows that implicit differentiation can yield the same result as explicit differentiation by comparing the two methods using the equation 2x + 3y = 7.
📝 Advanced Implicit Differentiation with Product Rules
The final paragraph deals with more complex scenarios in implicit differentiation, particularly when product rules are involved. It outlines the process of applying the product rule to functions like x * e^y and y * e^x, where the derivatives of each part of the product are calculated separately, and then combined according to the product rule. The paragraph demonstrates how to find y prime by solving a system of equations that results from differentiating the given functions implicitly. It concludes with a comprehensive example that ties together the concepts of implicit differentiation and the product rule.
Mindmap
Keywords
💡Implicit Differentiation
💡Explicit Function
💡Implicit Function
💡Independent Variable
💡Dependent Variable
💡Derivative
💡Power Rule
💡Chain Rule
💡Product Rule
💡Differentiation
💡y Prime (dy/dx)
Highlights
Introduction to the concept of implicit differentiation
Difference between explicit and implicit functions
Explicit functions clearly state y as a function of x
Implicit functions do not isolate y, implying it is a function of x
Derivative of an explicit function using basic differentiation rules
Derivative of an implicit function using power and chain rules
Substitution method to convert implicit to explicit functions for differentiation
Every derivative of y in an implicit function must be multiplied by y prime
Example of differentiating y to the fifth power using implicit differentiation
Solving for y prime in an implicit differentiation problem
Using implicit differentiation with the product rule for functions involving e^x and y^3
Solving for y prime in a product rule scenario with implicit differentiation
Demonstration of implicit differentiation yielding the same result as explicit differentiation
Differentiating a function that can be both implicit and explicit to show equivalence
Handling multiple product rules in implicit differentiation
Solving for y prime using algebraic techniques in implicit differentiation
Final answer format in terms of x's and y's after implicit differentiation
Upcoming video to include more examples of implicit differentiation
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: