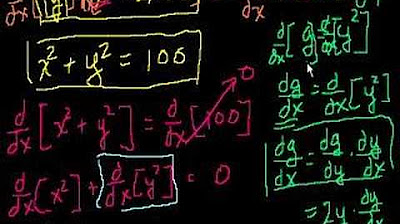Calculus 1 Lecture 2.7: Implicit Differentiation
TLDRThe video script delves into the concept of implicit differentiation, contrasting it with explicit forms of equations. It explains that while explicit functions directly express y in terms of x, implicit functions entwine y with x. The video demonstrates how to derive an implicit function without explicitly solving for y, using examples and highlighting the importance of treating y as a function of x. It also touches on the application of implicit differentiation in finding slopes and tangent lines at specific points on a curve, emphasizing the use of calculus and algebraic techniques like the product and quotient rules.
Takeaways
- 📝 Implicit differentiation is a method used to find the derivative of an equation when it's not possible to solve for y explicitly.
- 🔍 The process involves differentiating both sides of an implicit equation with respect to x, while treating y as a function of x.
- 📈 When differentiating, every term containing y will result in a dy/dx term due to the chain rule.
- 🌐 The derived equation can represent the slope of the curve at a given point or be used to find the equation of a tangent line.
- 🤔 It's important to note that implicit differentiation often results in an equation that still contains y, not a numerical value for the slope.
- 📚 The transcript provides an example where the derivative is found for the equation x^3 + y^3 = 5, resulting in dy/dx = -3x^2 / y^2.
- 🛠️ The method is useful for solving real-world problems, such as finding the rate of change of one quantity based on the rate of change of another related quantity.
- 🧩 The transcript also demonstrates how to take a second derivative using implicit differentiation and how to find the equation of a tangent line at a specific point.
- 👓 When solving for the equation of a tangent line, both x and y coordinates of the point are needed, and the resulting equation will be in terms of x and y.
- 📝 The process of implicit differentiation is shown to be applicable to various types of equations, including those involving products and quotients, requiring the use of product and quotient rules.
- 🎓 The transcript emphasizes the importance of understanding the rules of differentiation and the chain rule when performing implicit differentiation.
Q & A
What is implicit differentiation?
-Implicit differentiation is a method used in calculus to find the derivative of an equation when it is not possible or practical to solve for y as an explicit function of x. It involves differentiating both sides of an equation with respect to x, treating y as a function of x, and then solving for the derivative dy/dx.
What is the difference between explicit and implicit functions?
-An explicit function is one where y is isolated on one side of the equation and is expressed directly in terms of x. An implicit function, on the other hand, does not have y isolated on one side and is not written in the form y = f(x). Instead, it shows y as part of an equation that also involves x.
How can an implicit function sometimes define more than one function?
-An implicit function can define more than one function when the equation involves operations like square roots, which introduce plus and minus possibilities. For example, the equation y^2 = 4 - x^2 actually represents two distinct functions: y = sqrt(4 - x^2) and y = -sqrt(4 - x^2), which graph as an upper and lower half-circle respectively.
What is the general power rule used in implicit differentiation?
-The general power rule used in implicit differentiation states that when differentiating a term like y^n with respect to x, you bring down the exponent n and multiply by the derivative of the inside function, which is dy/dx. This rule is a specific application of the chain rule in calculus.
How does implicit differentiation relate to the chain rule?
-Implicit differentiation is closely related to the chain rule, as it often involves differentiating a function of x that is expressed in terms of y, or vice versa. The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In implicit differentiation, this often results in terms like dy/dx every time y is differentiated.
What is the quotient rule, and how is it applied in implicit differentiation?
-The quotient rule states that the derivative of a quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. In implicit differentiation, if you have a term with y in the numerator and x in the denominator, you would apply the quotient rule to find the derivative of that term.
Can you provide an example of how to use implicit differentiation to find the slope of a curve at a specific point?
-Consider the implicit equation y^2 = 4x. To find the slope (derivative dy/dx) at the point where x = 1, you would first differentiate both sides of the equation with respect to x, resulting in 2y( dy/dx ) = 4. If x = 1, then 4y( dy/dx ) = 4. If y is known at that point, say y = 2, you could solve for dy/dx, which would give you the slope of the curve at that point.
What is the product rule, and how is it applied in implicit differentiation?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In implicit differentiation, if you have a term that is the product of two functions of x (for example, x*y), you would apply the product rule to find the derivative of that term.
How can you find the equation of a tangent line at a specific point on a curve defined by an implicit equation?
-To find the equation of a tangent line at a specific point on a curve defined by an implicit equation, you first need to find the derivative (slope) of the curve at that point using implicit differentiation. Once you have the slope, you use the point-slope form of a line (y - y1 = m(x - x1)) where m is the slope and (x1, y1) is the given point. Plug in the values to get the equation of the tangent line.
What is the significance of implicit differentiation in practical applications?
-Implicit differentiation is significant in practical applications where the relationship between variables is not easily expressed in explicit form. It allows for the analysis of complex systems where variables are interconnected in ways that do not lend themselves to simple explicit functions. This method is particularly useful in fields like physics, engineering, and economics, where relationships between quantities are often implicit.
How does one handle a complex implicit differentiation problem that involves both product and quotient rules?
-For complex implicit differentiation problems that involve both product and quotient rules, one must apply each rule where appropriate. This involves carefully identifying terms in the equation that require the product rule (when a function of x is multiplied by a function of y) and the quotient rule (when one function of x is divided by another). It is crucial to maintain correct signs and to factor out common terms to simplify the resulting expression for dy/dx. This process may require multiple steps and careful algebraic manipulation.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, contrasting it with explicit forms of equations. It explains that while explicit equations solve for y in terms of x, implicit forms have y mixed with x. The speaker provides an example of transforming an implicit equation into an explicit one, highlighting that sometimes it's possible but not always straightforward. The main idea is to understand the difference between implicit and explicit functions and how they can be interconverted in certain cases.
🔄 Understanding Implicit and Explicit Functions
The speaker delves deeper into the concepts of implicit and explicit functions, using examples to illustrate the differences. They explain that an implicit equation cannot always be easily written in explicit form and may represent multiple functions, as seen in the case of a square root. The discussion emphasizes the importance of recognizing when an equation is implicit and the potential for it to define more than one function based on the variables involved.
🧠 Deriving Implicit Functions
This section focuses on the process of differentiating implicit functions. The speaker clarifies that even if an equation is implicit, it's possible to find its derivative without explicitly solving for y. The explanation includes the steps for implicit differentiation, emphasizing that y is treated as a function of x. The speaker also touches on the algebraic manipulation involved in simplifying the derived expressions, highlighting the use of derivatives and the importance of treating y as a function of x throughout the process.
📈 Implicit Differentiation and Derivatives
The speaker continues to elaborate on implicit differentiation, explaining that the derived expression is also implicit and contains the derivative of y with respect to x. They clarify the notation and process of solving for dy/dx, emphasizing the chain rule's role in implicit differentiation. The paragraph also discusses the importance of recognizing when an equation is implicit and the implications of taking derivatives on both sides of such equations.
🤔 Applications and Examples of Implicit Differentiation
This part of the script discusses the practical applications of implicit differentiation, providing examples to demonstrate the process. The speaker shows how to find the derivative of complex equations and solve for dy/dx, using the chain rule and general power rule. They also mention that implicit differentiation is not only useful for finding slopes of curves but also for understanding more complex calculus concepts involving multiple variables.
📝 Solving for dy/dx in Implicit Differentiation
The speaker guides the audience through the process of solving for dy/dx using implicit differentiation. They provide a step-by-step explanation, emphasizing the importance of understanding the algebraic manipulation involved. The paragraph includes examples that demonstrate how to handle complex terms and expressions when differentiating implicitly, and how to isolate dy/dx to find the derivative.
🌟 Further Examples and Practice
The speaker continues with more examples to reinforce the concept of implicit differentiation. They walk through the process of taking derivatives, applying rules like the product rule, and solving for dy/dx. The examples serve to illustrate the application of implicit differentiation in various scenarios and emphasize the importance of practice in mastering the technique.
🔢 Taking Second Derivatives and Implicit Applications
This section discusses taking second derivatives in the context of implicit differentiation. The speaker explains the process of differentiating the derivative of an equation to find the second derivative and provides an example to illustrate the steps involved. They also touch on the practical applications of implicit differentiation, such as finding tangent lines and slopes of curves at specific points.
📌 Implicit Differentiation and Tangent Lines
The speaker concludes the discussion on implicit differentiation by showing how to find the equation of a tangent line at a certain point on a curve defined by an implicit equation. They provide a detailed example, walking through the steps of taking the first and second derivatives, and using them to find the slope and equation of the tangent line. The explanation underscores the utility of implicit differentiation in solving real-world problems involving rates and slopes.
Mindmap
Keywords
💡Implicit Differentiation
💡Explicit Form
💡Derivative
💡Tangent Line
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Slope
💡Related Rates
💡Word Problems
Highlights
The introduction of implicit differentiation as a concept.
Comparison between explicit and implicit functions, and how they relate to solving for y.
The process of transforming an implicit function into an explicit one, if possible.
The importance of understanding that an implicit equation can define multiple functions.
The concept of taking a derivative without explicitly solving for y, which is the essence of implicit differentiation.
How to differentiate both sides of an equation with respect to x while treating y as a function of x.
The general power rule and its application in implicit differentiation.
The chain rule's significance in implicit differentiation and its impact on the resulting derivative.
The process of solving for dy/dx in an implicit differentiation problem.
The application of implicit differentiation in real-world scenarios, such as finding the slope of a curve at a given point.
The method of finding the equation of a tangent line at a specific point on a curve using implicit differentiation.
The explanation of how to handle complex fractions in implicit differentiation.
The demonstration of taking a second derivative using implicit differentiation.
The quotient rule's application in implicit differentiation and its effect on the derivative.
The product rule's application in implicit differentiation and its effect on the derivative.
The conclusion of the lesson and the encouragement for students to practice implicit differentiation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: