Particle motion problems - Calculus

vinteachesmath
31 Mar 202116:54
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Vin explores calculus motion problems involving a particle's movement along the x and y axes. He explains how to determine if a particle is speeding up or slowing down by analyzing velocity and acceleration at specific times. The video demonstrates using technology to find when a particle changes direction, calculate the position at given times, and measure total distance traveled. It concludes with a discussion on displacement, offering a comprehensive guide to solving related calculus problems.

Takeaways
  • 📚 The video is a tutorial on calculus motion problems, focusing on understanding the motion of particles along an axis using mathematical functions.
  • 🔍 The first example discusses a particle moving along the x-axis with a given velocity function, aiming to determine if the particle is speeding up or slowing down at a specific time.
  • 📈 To analyze the particle's motion, the presenter uses technology to find the velocity and acceleration at time t equals 4, using the concepts of derivatives to understand changes in motion.
  • 🛑 The particle is found to be slowing down at t=4 because the velocity is positive but the acceleration is negative, indicating a deceleration.
  • 🔄 The video explains how to find the times when the particle changes direction by looking for when the velocity function crosses zero, indicating a reversal in motion.
  • 📉 The particle changes direction at t=2.707 and t=3.394, as determined by the velocity function equaling zero at these times.
  • 📝 The position of the particle at time t=0 is found by using the fundamental theorem of calculus, integrating the velocity function from 0 to 4 and using the known position at t=4.
  • 🚀 The total distance traveled by the particle from t=0 to t=3 is calculated by integrating the absolute value of the velocity function, accounting for both forward and backward movements.
  • 🆕 The second example involves a particle moving along the y-axis, with the presenter explaining how to determine the direction of motion at a specific time t=1.5.
  • ⏫ The direction of motion is determined by the sign of the velocity at t=1.5, with a positive value indicating upward motion.
  • 📊 The acceleration at t=1.5 is found to be negative, indicating that the velocity is decreasing at that time.
  • 📌 The position of the particle at t=2 is calculated using the initial position and the integral of the velocity function from 0 to 2, providing the vertical displacement from the origin.
Q & A

  • What is the primary focus of the video?

    -The video focuses on solving calculus motion problems, specifically analyzing the velocity and acceleration of particles moving along the x-axis and y-axis.

  • What is the significance of the velocity function in determining the particle's motion?

    -The velocity function tells us how fast the particle is moving and in which direction at any given time. It is crucial for determining whether the particle is speeding up, slowing down, or changing direction.

  • How can you determine if a particle is speeding up or slowing down?

    -You can determine if a particle is speeding up or slowing down by comparing the signs of its velocity and acceleration. If both are positive or both are negative, the particle is speeding up. If the signs are different, the particle is slowing down.

  • What is the relationship between acceleration and the rate of change of velocity?

    -Acceleration is the derivative of velocity, which means it represents the rate of change of velocity. A positive acceleration indicates an increase in velocity, while a negative acceleration indicates a decrease.

  • How does the position function relate to the velocity function?

    -The position function is the antiderivative of the velocity function. It tells us the location of the particle at any given time and can be found by integrating the velocity function.

  • What is the significance of finding the velocity function equal to zero?

    -Finding when the velocity function equals zero helps determine the times when the particle changes direction. The velocity function crossing the x-axis indicates a change from moving in one direction to the other.

  • How can you find the position of a particle at a specific time?

    -You can find the position of a particle at a specific time by evaluating the position function at that time. Alternatively, you can use the fundamental theorem of calculus to find the difference in position between two times.

  • What is the difference between total distance traveled and displacement?

    -Total distance traveled is the sum of all distances covered by the particle, regardless of direction, and is found by integrating the absolute value of velocity. Displacement, on the other hand, is the net change in position from the starting point to the final position and is found by integrating the velocity function.

  • How does the video demonstrate the use of technology in solving calculus problems?

    -The video demonstrates the use of a calculator to find values of functions, their derivatives, and integrals. It shows how to use technology to evaluate functions at specific points, find roots, and calculate definite integrals.

  • What is the fundamental theorem of calculus, and how is it applied in the video?

    -The fundamental theorem of calculus connects differentiation and integration. It states that the integral of a function can be found by evaluating its antiderivative at the limits of integration. In the video, it is used to find the position of a particle at a specific time by evaluating the antiderivative of the velocity function.

Outlines
00:00
📚 Introduction to Calculus Motion Problems

Vin introduces the topic of calculus motion problems focusing on two examples involving a particle's movement along the x-axis and its velocity and acceleration. The first problem examines the particle's speed and direction change at a specific time by calculating velocity and acceleration using a given function. The explanation covers how to determine if the particle is speeding up or slowing down based on the signs of these values.

05:01
🔍 Analyzing Particle's Motion and Direction Changes

This section delves into finding the exact times when the particle changes direction by looking for when the velocity function crosses zero within a given time interval. The process involves adjusting the graph's view for clarity and using the calculator to find the roots of the velocity function, indicating the points of direction change. The summary includes the specific times at which the direction changes occur.

10:01
📈 Calculating Position and Total Distance Traveled

The third paragraph discusses calculating the position of the particle at time t equals zero by using the anti-derivative of the velocity function and applying the fundamental theorem of calculus. It also covers finding the total distance traveled by the particle from t equals zero to t equals three, which involves integrating the absolute value of the velocity function to account for both forward and backward movements.

15:03
📉 Vertical Motion and Displacement Calculation

The final paragraph addresses a vertical motion scenario, starting with determining the particle's direction of movement at a specific time by evaluating the velocity function. It continues with finding the acceleration and explains the relationship between velocity and acceleration in terms of increasing or decreasing speed. Lastly, it covers calculating the position of the particle at a later time and the displacement from the start to the end of the time interval, emphasizing the difference between total distance and displacement.

Mindmap
Keywords
💡Particle
In the context of the video, a 'particle' refers to a point object that moves along an axis, representing a simplified model for studying motion. It is a fundamental concept in physics and is used to analyze the motion of objects without considering their size or shape. The video discusses the motion of a particle along the x-axis and y-axis, illustrating its velocity and acceleration at different times.
💡Velocity Function
The 'velocity function' is a mathematical representation of the speed of an object at any given time. It is a key concept in the video, as it is used to determine how fast the particle is moving at various points in time. The script mentions finding the velocity at specific times, such as at t equals 4 seconds, using the function 1 plus 2 sine of t squared divided by 2.
💡Acceleration
Acceleration is the rate of change of velocity with respect to time. It indicates whether an object is speeding up or slowing down. In the video, the concept of acceleration is used to analyze the motion of the particle, with the script showing how to calculate acceleration by taking the derivative of the velocity function and evaluating it at t equals 4.
💡Position Function
The 'position function' describes the location of the particle at any given time. It is the integral of the velocity function and is used to find the displacement of the particle over a time interval. The video explains how to find the position of the particle at time t equals 0 by using the position function and the fundamental theorem of calculus.
💡Direction Change
A 'direction change' occurs when the velocity of the particle crosses through zero, indicating a reversal in the direction of motion. The video script discusses finding the times when the particle changes direction by looking for when the velocity function equals zero within a specific interval, such as from 0 to 4 seconds.
💡Anti-Derivative
An 'anti-derivative' is a function that reverses the process of differentiation. It is used to find the position function from the velocity function. The video explains the process of taking the anti-derivative to determine the position of the particle at time t equals zero, using the information given about the particle's position at t equals 4.
💡Displacement
Displacement refers to the change in position of an object. It is a vector quantity that represents the shortest distance from the initial to the final position, with direction. The video script calculates the displacement of the particle from t equals 0 to t equals 2 by integrating the velocity function over this interval.
💡Total Distance Traveled
The 'total distance traveled' is the sum of the distances covered by the particle during its motion, regardless of direction. The video distinguishes between distance and displacement, emphasizing that distance is always positive and includes the absolute value of the velocity function when calculating it from t equals 0 to t equals 3.
💡Chain Rule
The 'chain rule' is a fundamental theorem in calculus used to compute the derivative of a composite function. Although not explicitly mentioned in the transcript, the process of finding the derivative of the velocity function to determine acceleration would likely involve the chain rule, especially when dealing with functions of functions, such as sine of t squared.
💡Sign Change
A 'sign change' in the context of the video refers to the transition of a function's value from positive to negative or vice versa. The script discusses how sign changes in the velocity function indicate changes in the direction of the particle's motion, which is crucial for understanding when the particle reverses direction.
Highlights

Introduction to calculus motion problems and the concept of velocity and acceleration in determining if a particle is speeding up or slowing down.

Explanation of how to determine if a particle is moving left or right along the x-axis using the position function.

Demonstration of using technology to find velocity and acceleration at a specific time, t=4, to analyze the particle's motion.

Calculation of velocity at 4 seconds using a calculator view, revealing a velocity of 2.9787.

Derivation of acceleration by finding the derivative of the velocity function and its interpretation at t=4.

Analysis of results showing positive velocity and negative acceleration, indicating the particle is slowing down at t=4.

Method to find times when the particle changes direction by looking for when the velocity function equals zero.

Use of calculator to graph and find roots of the velocity function on the interval from 0 to 4.

Identification of two times, t=2.707 and t=3.394, where the particle changes direction.

Concept of finding the position of the particle at time t=0 using the anti-derivative of the velocity function.

Application of the fundamental theorem of calculus to find the position at t=0 by evaluating a definite integral.

Calculation of the position at t=0, resulting in a value of -3.815, indicating the starting point of the particle.

Explanation of finding the total distance traveled by a particle by integrating the absolute value of velocity.

Calculation of the total distance traveled from t=0 to t=3, yielding a result of 5.301 units.

Introduction to a second problem involving vertical motion along the y-axis and determining direction at t=1.5.

Analysis of the velocity function to determine if the particle is moving up or down at a specific time, t=1.5.

Calculation of acceleration at t=1.5 and its interpretation to understand if the particle's velocity is increasing or decreasing.

Determination of the position of the particle at t=2 using the initial position and the integral of the velocity function.

Calculation of the displacement of the particle from t=0 to t=2 by integrating the velocity function over the interval.

Conclusion summarizing the approach to solving calculus motion problems and encouraging viewer engagement.

Transcripts

Browse More Related Video

Particle MotionDay1

Calculus AB Homework 5.3: Position, Velocity, Acceleration

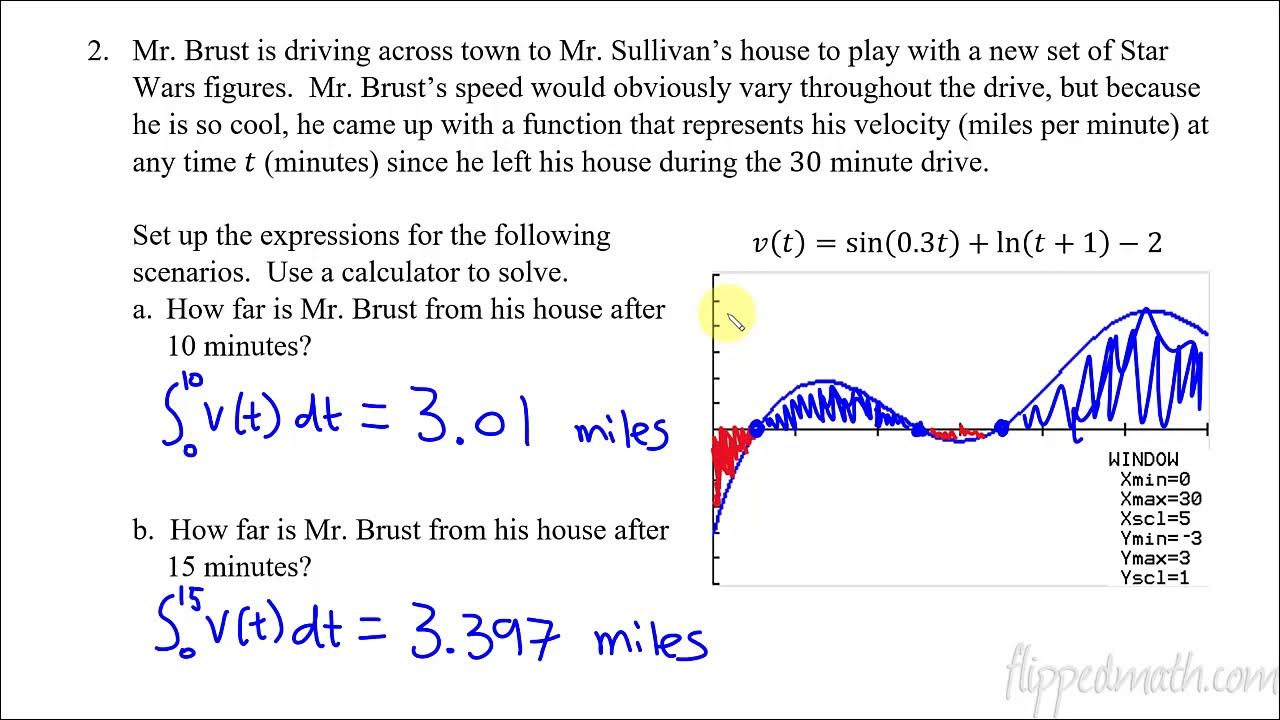
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

2011 AP Calculus AB Free Response #1

Fall 2023 MNC: Motion "wellness" - velocity, speed, acceleration, distance, position

AP Calculus BC Lesson 9.6

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus MotionParticle MovementVelocity AnalysisAccelerationDirection ChangePosition FunctionAnti-DerivativeIntegral CalculusDisplacementEducational Content