AP Calculus BC Lesson 9.6

Elizabeth Fein

22 Apr 202324:33

EducationalLearning

32 Likes 10 Comments

TLDRIn this lesson, the application of parametric equations and vector-valued functions to particle motion within the context of the AP Calculus exam is explored. Key formulas for velocity, acceleration, speed, displacement, and arc length are reviewed. The video delves into solving problems involving finding velocity and acceleration vectors, determining when a particle is at rest, calculating the total distance traveled, and identifying specific points on the particle's path. The use of derivatives and integrals is emphasized in solving these problems, with a focus on understanding the mathematical concepts and their practical applications.

Takeaways

📚 The lesson focuses on applying parametric equations and vector-valued functions to particle motion problems in the context of the AP Calculus exam.
🌟 Velocity is the first derivative of position and acceleration is the second derivative of position, with speed represented as the square root of the sum of the squares of the rate of change of position components.
📈 Displacement between two times is given by the integral of velocity from the initial to the final time, while arc length is the integral of the speed over time.
🎯 To find the new position, integrate the velocity from the initial time to the desired time and add it to the initial position.
🚫 A particle is at rest when both its x and y rate of change components (dx/dt and dy/dt) are zero.
🔄 The position of a particle in the XY plane is given by parametric equations, and the velocity vector can be obtained by differentiating these equations.
🕒 Specific problems in the lesson involve calculating the velocity vector at a given time, the acceleration vector, determining when a particle is at rest, and finding the total distance traveled.
📊 The script provides examples of how to set up and solve for various particle motion scenarios using calculus concepts and integrals.
🛤️ Arc length is calculated using the integral of the speed, which is derived from the square root of the sum of the squares of the derivatives of the position functions.
📌 The script emphasizes the importance of understanding the context of particle motion and the application of vector calculus to solve problems on the AP Calculus exam.
📝 The lesson concludes with a calculator-free response question that tests the understanding of the concepts taught, including finding the velocity vector, acceleration vector, speed, and the time at which certain conditions are met for a particle in motion.

Q & A

What is the main focus of Lesson 9.6 in the video?
-The main focus of Lesson 9.6 is to apply knowledge of parametric equations and vector-valued functions to the context of particle motion on the AP Calculus exam.
How is velocity related to position in particle motion?
-Velocity is the derivative of position, representing the rate of change of position with respect to time.
What is the formula for calculating the speed of a particle at any time T?
-The speed of a particle at any time T can be represented by the square root of (x'(t)^2 + y'(t)^2), where x'(t) and y'(t) are the derivatives of the x and y components of the position vector, respectively.
How is displacement from time T1 to T2 represented in the context of particle motion?
-Displacement from time T1 to T2 is represented by the integral from T1 to T2 of the velocity vector V(t) dt.
What is the significance of arc length in the context of particle motion?
-Arc length represents the total distance traveled by the particle and is calculated as the integral from time T1 to T2 of the square root of (dx/dt)^2 + (dy/dt)^2 dt.
How can you find the velocity vector of a particle at a specific time T, given its position vector?
-To find the velocity vector at a specific time T, you take the derivative of the position vector with respect to time.
What is the acceleration vector of a particle, and how is it related to the velocity vector?
-The acceleration vector is the derivative of the velocity vector, which can also be thought of as the second derivative of the position vector with respect to time.
How can you determine if a particle is at rest at a certain time?
-A particle is at rest if both its x and y components of velocity (dx/dt and dy/dt) are equal to zero at a certain time.
What is the relationship between the total distance traveled and the speed of a particle?
-The total distance traveled is found by integrating the speed (the magnitude of the velocity vector) over a time interval, without the need for absolute value signs since the square root ensures non-negativity.
How do you calculate the distance of a particle from the origin at a specific time, given its position vector?
-To calculate the distance from the origin, you find the x and y components of the position vector at the specific time, then use the Pythagorean theorem to find the hypotenuse of the right triangle formed by these components.
What is the significance of finding the tangent line's slope at a specific point on a particle's path?
-Finding the slope of the tangent line at a specific point gives insight into the direction and steepness of the path at that particular location, which can be used to analyze the motion characteristics of the particle.

Outlines

00:00

📚 Lesson 9.6: Parametric Equations and Vector-Valued Functions in Motion

This paragraph introduces Lesson 9.6, focusing on applying parametric equations and vector-valued functions to the context of particle motion in the AP Calculus exam. It emphasizes the importance of understanding how velocity and acceleration are derived from position functions and how to calculate speed, displacement, and arc length. The lesson also covers the concept of a particle being at rest and provides a method for solving problems involving these concepts.

05:01

🚀 Calculating Velocity and Acceleration Vectors

The paragraph delves into the calculation of velocity and acceleration vectors for a particle moving in the XY plane. It explains how to find the velocity vector by differentiating the position vector and how to calculate the acceleration vector by differentiating the velocity vector. The paragraph includes specific examples with given parametric equations and demonstrates the process of finding the velocity and acceleration at particular times.

10:02

🧭 Determining Rest and Motion States

This section focuses on identifying when a particle is at rest by setting the derivatives of position (DX/DT and DY/DT) to zero. It provides a method for finding the times when a particle is not moving by solving these equations. The paragraph also explains how to determine the point at which a particle is at rest by evaluating the position functions at the times found.

15:06

📏 Measuring Distance and Speed

The paragraph discusses how to calculate the distance of a particle from the origin at a given time and the total distance traveled between two times. It explains the process of integrating the velocity vector to find the arc length and how to use the Pythagorean theorem to find the distance from the origin. Additionally, it covers how to find the speed of a particle at a specific time by taking the square root of the sum of the squared derivatives of the position functions.

20:06

🔍 Analyzing Tangent Slope and Arc Length

This paragraph addresses the calculation of the slope of the tangent line to the particle's path and the determination of the total distance traveled. It provides a method for finding the time at which the slope of the tangent line is equal to a given value by setting up and solving equations involving the derivatives of the position functions. The paragraph also explains how to calculate the arc length of the particle's path over a specified time interval.

Mindmap

Keywords

💡Parametric Equations

Parametric equations are mathematical equations that describe the path of a moving object in terms of a parameter, usually time. In the video, parametric equations are used to represent the position of a particle in the XY plane, with the particle's coordinates being functions of time. This concept is crucial for understanding the motion of the particle and calculating its velocity and acceleration at different times.

💡Vector-Valued Functions

A vector-valued function is a function that returns a vector as its output. In the context of the video, vector-valued functions are used to describe the position, velocity, and acceleration of a particle in motion. These functions assign a vector to each value of the parameter (time), allowing for a comprehensive representation of the particle's motion.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position. It has both magnitude (speed) and direction. In the video, velocity is calculated as the derivative of the position function with respect to time. This concept is essential for understanding how fast an object is moving and in which direction.

💡Acceleration

Acceleration is the rate of change of velocity over time. It is a vector quantity that describes how quickly an object's velocity is changing. In the context of the video, acceleration is found by taking the derivative of the velocity function, which is itself the derivative of the position function.

💡Speed

Speed is the magnitude of the velocity vector and represents the rate of motion of an object without considering direction. It is a scalar quantity and can be calculated as the square root of the sum of the squares of the components of the velocity vector.

💡Displacement

Displacement refers to the change in position of an object from its initial location to its final location. It is a vector quantity that has both magnitude and direction. In the video, displacement is calculated as the integral of the velocity function over a time interval, representing the straight-line distance between two points in the path of motion.

💡Arc Length

Arc length is the total distance traveled by an object along its path of motion. It differs from displacement in that it accounts for the actual path taken rather than the direct line between two points. In the context of the video, arc length is found by integrating the speed of the particle over a time interval.

💡Derivative

In calculus, a derivative represents the rate of change of a function with respect to its independent variable. It is used to find the slope of a curve at any point, which can be thought of as the velocity or speed in the context of motion. The video uses derivatives to find both the velocity and acceleration of a particle from its position function.

💡Integral

An integral in calculus represents the accumulation of a quantity over an interval. It is used to find the area under a curve, the total distance traveled (arc length), or the displacement of an object. In the video, integrals are used to calculate displacement and arc length for a particle in motion.

💡Particle Motion

Particle motion refers to the movement of a point mass, or particle, along a path in space over time. The video focuses on applying mathematical concepts such as parametric equations, derivatives, and integrals to analyze and describe the motion of a particle in the context of the AP Calculus exam.

Highlights

The lesson focuses on applying parametric equations and vector-valued functions to particle motion in the context of the AP Calc exam.

Velocity is the derivative of position and acceleration is the second derivative of position.

The speed of a particle at any time T can be represented by the square root of the sum of the squares of its derivatives with respect to time.

Displacement from time T1 to T2 is given by the integral of the velocity vector from T1 to T2.

Arc length, representing total distance traveled, is calculated as the integral of the speed from T1 to T2.

When a particle is at rest, its derivatives DX/DT and DY/DT are both equal to zero.

To find the new position, integrate the velocity vector from the initial time to the desired time.

The velocity vector of a particle moving in the XY plane is given by the derivative of its position vector.

The acceleration vector is found by taking the derivative of the velocity vector.

A particle is at rest at the time when both its x and y derivatives are zero.

The total distance traveled by a particle is found using the arc length formula.

The distance of a particle from the origin is calculated using the Pythagorean theorem.

The slope of the tangent line to a particle's path is given by the ratio of the derivatives of the position vector components.

The speed of a particle is calculated using the magnitude of the velocity vector.

The time at which a particle's path has a specific slope can be found by setting the ratio of derivatives equal to the desired slope and solving for time.

The total distance traveled by a particle along a curve is found using the arc length formula applied to the parametric equations of the curve.

The x coordinate of a particle's position at a given time is found by integrating its x component from a known initial time to the desired time.

The time at which a particle has a specific speed is found by setting the magnitude of the velocity vector equal to the desired speed and solving for time.

The time at which the slope of the tangent line to a particle's path is a specific value is found by setting the ratio of the derivatives of the position vector components equal to that value and solving for time.

Transcripts

Browse More Related Video

Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

Equations of Motion

2022 Live Review 6 | AP Calculus BC | Working with Parametric Equations and Vectors

2023 AP Calculus BC Free Response Question #2

Polar, Parametric, Vector Multiple Choice Practice for Calc BC (Part 1)

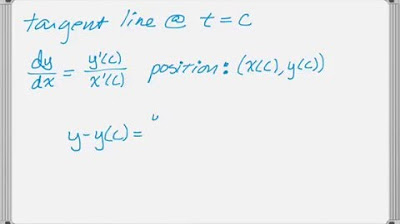
AP Calculus BC Parametric and Vector AP Exam Review

Related Tags

AP Calculus Parametric Equations Vector Functions Particle Motion Velocity Calculation Acceleration Vector Arc Length Integral Calculus Exam Prep Math Education Video Tutorials