Particle MotionDay1

Chad Gilliland
20 Oct 201315:00
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script explores the relationship between position, velocity, and acceleration in particle motion. It demonstrates how to calculate velocity and acceleration from a given position function and interprets these values to determine when a particle is at rest, moving left, or right. The script also covers finding displacement and distance traveled, as well as identifying intervals of speeding up and slowing down based on the signs of velocity and acceleration. The explanation is supported by mathematical derivations and graphical illustrations, making it an informative resource for understanding kinematic principles.

Takeaways
  • 📚 The lesson is about the relationship between position, velocity, and acceleration in particle motion.
  • 🚀 The particle moves along a horizontal line, with its position described by the function s(t) where s is in meters and t is in seconds.
  • 🔍 To find the velocity at time T, the first derivative of position s'(t) is calculated, resulting in 6t^2 - 14t + 4.
  • ⏱ The velocity at one second is found by substituting t = 1 into the velocity equation, yielding a velocity of -4 m/s.
  • 🔄 The particle is at rest when its velocity is zero, which occurs at t = 1/3 and t = 2 seconds.
  • 📉 The particle moves to the left when its velocity is negative and to the right when its velocity is positive.
  • 🔢 The acceleration is the second derivative of position, calculated as 12t - 14, and at t = 1, it is -2 m/s².
  • 📍 The displacement of the particle between t = 0 and t = 3 is found by subtracting s(0) from s(3), resulting in 3 meters to the right.
  • 🛣 The total distance traveled by the particle is calculated by considering the absolute value of the changes in position, summing to 12.2592 meters.
  • 🔄 The particle speeds up when the velocity and acceleration have the same sign and slows down when they have opposite signs.
  • 📉 The critical points for velocity and acceleration help determine the intervals of speeding up and slowing down in the particle's motion.
Q & A

  • What is the main topic discussed in the script?

    -The main topic discussed in the script is the relationship between position, velocity, and acceleration in the context of particle motion along a horizontal line.

  • What is the position function given for the particle?

    -The position function for the particle is given by \( s(T) = 6T^2 - 14T + 4 \), where \( s \) is measured in meters and \( T \) is measured in seconds.

  • How is the velocity of the particle at time T calculated?

    -The velocity of the particle at time T is calculated as the first derivative of the position function, which is \( v(T) = 6T^2 - 14T + 4 \).

  • What is the velocity of the particle at T equals 1 second?

    -The velocity of the particle at T equals 1 second is found by substituting T with 1 in the velocity function, resulting in \( v(1) = 6(1)^2 - 14(1) + 4 = -4 \) meters per second.

  • When is the particle at rest according to the script?

    -The particle is at rest when the velocity equals zero. By setting the velocity function equal to zero and solving, the particle is at rest at \( T = \frac{1}{3} \) and \( T = 2 \) seconds.

  • In which direction is the particle moving when it is at rest?

    -The particle is not moving in any direction when it is at rest. It is simply stationary at the points \( T = \frac{1}{3} \) and \( T = 2 \) seconds.

  • How does the script determine when the particle is moving left or right?

    -The script uses a number line test with the factored velocity function to determine the intervals where the particle is moving left (negative velocity) or right (positive velocity).

  • What is the acceleration function of the particle?

    -The acceleration function of the particle is the second derivative of the position function, which is \( a(T) = 12T - 14 \).

  • What is the displacement of the particle between T equals 0 and T equals 3?

    -The displacement of the particle between T equals 0 and T equals 3 is found by calculating \( s(3) - s(0) \), which results in a displacement of 3 meters to the right.

  • How is the total distance traveled by the particle calculated?

    -The total distance traveled by the particle is calculated by considering the absolute value of the changes in position at critical points and endpoints, resulting in a total distance of 12.2592 meters.

  • What does the script say about the particle's speed and when it is speeding up or slowing down?

    -The script explains that speed is the absolute value of velocity and is always positive. The particle is speeding up when velocity and acceleration have the same sign and slowing down when they have opposite signs.

Outlines
00:00
🔍 Particle Motion Analysis

This paragraph introduces the concept of particle motion, focusing on the relationship between position, velocity, and acceleration. The position of a particle moving along a horizontal line is given by the function s(T) = 6T^2 - 14T + 4, where s is in meters and T is in seconds. The velocity, the first derivative of position, is calculated as v(T) = 12T - 14. The particle's velocity at T=1 second is found to be -4 m/s, indicating movement to the left. The particle is at rest when v(T) = 0, which occurs at T = 1/3 and T = 2. A number line test is used to determine the direction of movement, showing the particle moves to the right on intervals (0, 1/3) and (2, ∞), and to the left on the interval (1/3, 2).

05:02
📊 Calculating Acceleration and Displacement

The second paragraph delves into calculating the acceleration of the particle, which is the second derivative of its position, resulting in a(T) = 12T - 14. The acceleration at T=1 second is -2 m/s². The displacement of the particle from T=0 to T=3 is determined by subtracting the position at T=0 from the position at T=3, yielding a displacement of 3 meters to the right. The distance traveled, which accounts for the total path length regardless of direction, is calculated by considering the changes in position at critical points where the velocity is zero, resulting in a total distance of 12.2592 meters.

10:04
🚀 Understanding Speed and Acceleration Dynamics

The final paragraph discusses the concept of speed, defined as the absolute value of velocity, which is always positive. It explains how to determine when the particle is speeding up or slowing down based on the signs of velocity and acceleration. Critical points for both velocity and acceleration are identified, including when the acceleration is zero at T = 7/6. The intervals of speeding up and slowing down are determined by comparing the signs of velocity and acceleration, revealing that the particle speeds up on the intervals (1/3, 7/6) and (2, ∞), and slows down on the intervals (0, 1/3) and (7/6, 2).

Mindmap
Keywords
💡Particle Motion
Particle motion refers to the movement of a small object along a path, in this case, a horizontal line. The video explores how this motion is described by position, velocity, and acceleration functions. The script illustrates this with a particle moving either to the right or left along the line.
💡Position Function
The position function, denoted as s(t), gives the location of the particle at any time t. In the video, s(t) is measured in meters and t in seconds. Understanding this function is crucial as it serves as the basis for determining the particle's velocity and acceleration.
💡Velocity
Velocity, represented as V(t), is the rate of change of position with respect to time. It is the first derivative of the position function. The video explains how to calculate the velocity at any time t, and specifically at t = 1 second, where V(1) is found to be -4 meters per second, indicating the particle is moving left.
💡Acceleration
Acceleration, represented as A(t), is the rate of change of velocity with respect to time. It is the second derivative of the position function. The video demonstrates how to find the acceleration at any time t and specifically at t = 1 second, where A(1) is -2 meters per second squared, indicating deceleration.
💡Rest
The particle is at rest when its velocity is zero. The video shows how to solve for the times when V(t) = 0, which occurs at t = 1/3 and t = 2 seconds. These points are critical as they indicate moments when the particle changes direction.
💡Moving Left
The particle moves left when its velocity is negative. In the video, this is analyzed using a number line to determine intervals where V(t) < 0. The particle moves left between t = 1/3 and t = 2 seconds.
💡Moving Right
The particle moves right when its velocity is positive. The video uses a number line test to identify these intervals. The particle moves right from 0 to 1/3 seconds and from 2 seconds onwards.
💡Displacement
Displacement refers to the change in position of the particle over a period of time. It is calculated as the difference between the position at two times. In the video, the displacement from t = 0 to t = 3 seconds is shown to be 3 meters to the right.
💡Distance Traveled
Distance traveled is the total length of the path the particle has moved, regardless of direction. Unlike displacement, it accounts for all movements back and forth. The video calculates the total distance traveled by adding up movements in different intervals, resulting in a distance of 12.2592 meters.
💡Speed
Speed is the absolute value of velocity, always positive, representing how fast the particle is moving without regard to direction. The video distinguishes between speeding up and slowing down based on whether velocity and acceleration have the same or opposite signs.
Highlights

Introduction to particle motion and its relation to position, velocity, and acceleration.

Explanation of horizontal particle movement and its position function s(T).

Derivation of velocity V(T) as the first derivative of position s(T).

Calculation of velocity at T equals one second, resulting in negative four meters per second.

Determination of particle rest states by setting velocity to zero and solving for T.

Identification of rest times at T equals one-third and T equals two seconds.

Use of a number line to determine the direction of particle movement (left or right).

Analysis of intervals where the particle moves left or right based on velocity signs.

Derivation of acceleration as the second derivative of position, resulting in 12t - 14.

Calculation of acceleration at T equals one, resulting in negative two meters per second squared.

Explanation of displacement as the difference between final and initial positions.

Calculation of displacement resulting in three meters to the right.

Determination of distance traveled by considering changes in particle direction.

Calculation of total distance traveled as twelve point two five nine two meters.

Introduction to the concept of speed as the absolute value of velocity.

Analysis of speeding up and slowing down intervals based on the signs of velocity and acceleration.

Conclusion summarizing the particle's motion, rest, and direction changes over time.

Transcripts

Browse More Related Video

Calculus - Position Average Velocity Acceleration - Distance & Displacement - Derivatives & Limits

Particle motion problems - Calculus

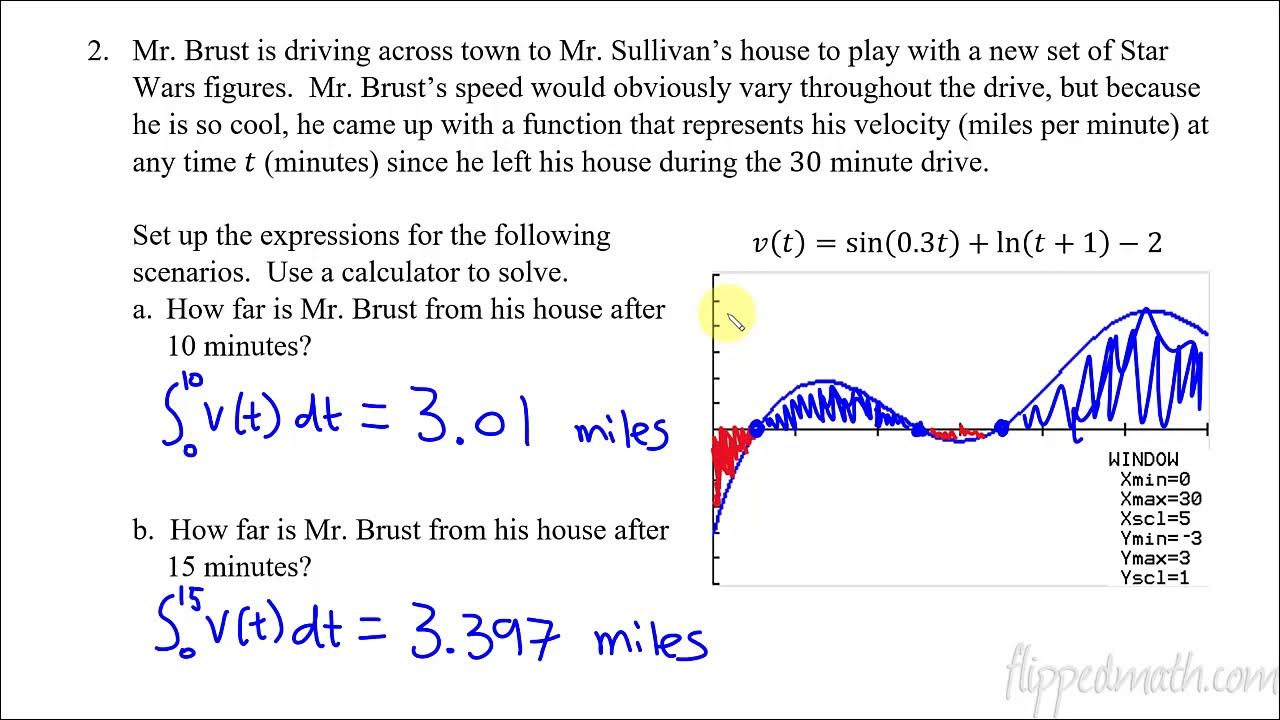
Calculus AB/BC – 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals

Slowing Down Speeding Up Derivatives Application Calculus MCV4U

Particle Motion Day 2

Particle Motion - Speeding Up and Slowing Down (Example, AP Calculus)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Particle MotionPhysics TutorialVelocity AnalysisAcceleration CalculationDisplacement ConceptMotion DynamicsEducational ContentKinematics StudyCritical PointsDirection Change