PLT: Lambda Calculus - Basics 3 (Operations on church numerals)

Rehno Lindeque
12 Mar 201105:32
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of Church numerals and the successor function in lambda calculus. It demonstrates how to increment a number by one using lambda notation, introduces the plus function, and briefly touches on multiplication and exponentiation. The script aims to illustrate the beauty and simplicity of lambda calculus through these examples.

Takeaways
  • 📝 The video script discusses the continuation of a previous video on YouTube about the successor function in lambda calculus.
  • 🔢 Church numerals are introduced as a way to represent numbers in lambda calculus, using functions to represent each numeral.
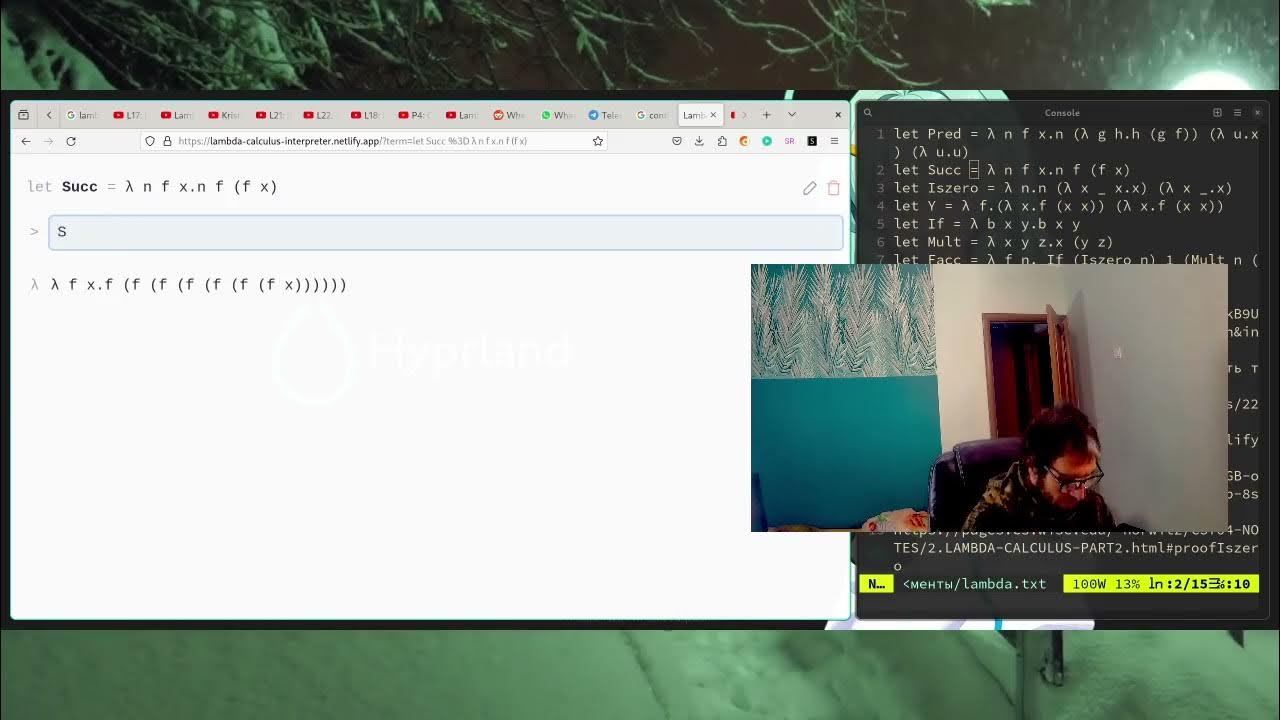
  • 🔄 The successor function is defined and demonstrated with an example, showing how to increment a Church numeral by one.
  • 💡 Lambda notation is used to describe the successor function, with a focus on the substitution of variables within the function.
  • 👨‍🏫 The script attempts to explain the process of applying the successor function to the Church numeral 'one', using lambda calculus terminology.
  • 🔑 The concept of 'lambda abstraction' is introduced, which is a fundamental concept in lambda calculus for creating anonymous functions.
  • 🤔 The script suggests defining additional functions in lambda calculus, such as 'plus', 'multiply', and 'power', but does not provide examples for these.
  • 🔗 The definition of the 'plus' function in lambda calculus is given, showing how it can be constructed using lambda abstraction and the successor function.
  • 🔄 The script highlights the recursive nature of the 'plus' function, where the successor is applied M times to N.
  • 🔍 The 'multiply' and 'power' functions are briefly mentioned, indicating that they can also be defined using lambda calculus, but without detailed explanation.
  • 📚 The presenter expresses an intention to provide examples of the 'power' function in a subsequent video or part of the lecture.
Q & A

  • What is the main topic discussed in the video script?

    -The main topic discussed in the video script is the concept of the successor function and other basic arithmetic functions in lambda calculus, including how to define and use them.

  • What are Church numerals?

    -Church numerals are a way of representing natural numbers in lambda calculus, where each numeral is a higher-order function.

  • How is the successor function defined in the script?

    -The successor function is defined as a lambda expression that takes a function 'F' and an argument 'X', and applies 'F' to 'X'.

  • What is the lambda expression for the successor of one?

    -The lambda expression for the successor of one is 'lambda F X. F (F X)', which applies 'F' twice to 'X'.

  • How does the script explain the process of incrementing a Church numeral by one?

    -The script explains that by applying the successor function to a Church numeral, you effectively increment that numeral by one.

  • What are the three additional functions mentioned in the script?

    -The three additional functions mentioned in the script are for addition, multiplication, and exponentiation.

  • How is the addition function represented in lambda calculus in the script?

    -The addition function is represented as 'lambda M N F X. M F (N F X)', which applies 'M' to 'F' and then applies the result 'N' times to 'F X'.

  • What is the multiplication function defined as in the script?

    -The multiplication function is defined as 'lambda M N. M (N F)', which applies the second number 'N' to the successor function 'M' times.

  • What is the exponentiation function in lambda calculus as described in the script?

    -The exponentiation function is described as 'B to the power of E', which is represented as 'E B' in lambda calculus, indicating that 'B' is applied 'E' times.

  • Why does the script mention that applying the successor function M times is equivalent to addition?

    -The script mentions this because applying the successor function M times to a number is the same as adding 'M' to that number, which is a fundamental concept in lambda calculus for defining addition.

  • What is the significance of the script's mention of 'applying successor M times' in the context of lambda calculus?

    -The significance lies in demonstrating how repeated application of the successor function can be used to build more complex arithmetic operations, such as addition, in lambda calculus.

Outlines
00:00
📚 Introduction to Church Numerals and Successor Function

The speaker begins by discussing the continuation from a previous video, focusing on Church numerals and the successor function. They explain that Church numerals are a way to represent numbers in lambda calculus and that the successor function is used to increment a number by one. The speaker provides an example of how the successor function works by taking the successor of one, which is essentially applying the function to itself twice. They also introduce the concept of lambda notation and how it can be used to represent numbers and functions. Additionally, the speaker briefly mentions the definitions of three more functions: addition, multiplication, and exponentiation, without going into examples.

05:03
🔢 Defining Addition, Multiplication, and Exponentiation in Lambda Calculus

In this paragraph, the speaker quickly defines the addition, multiplication, and exponentiation functions in lambda calculus. They explain that addition is represented by a lambda function that takes two numbers, M and N, and applies the successor function M times to N. This essentially adds M to N. Multiplication is defined similarly, where M times N is represented by applying the addition function M times to N. Exponentiation is also briefly mentioned, but the speaker does not provide a detailed explanation or example for this function. The speaker emphasizes the beauty of these definitions and how they make sense in the context of lambda calculus.

Mindmap
Keywords
💡Successor Function
The successor function in the context of the video refers to a function in lambda calculus that takes a number and returns the next number in the sequence. It's a fundamental concept in the Church numerals system, where numbers are represented as functions. In the script, the successor of one is explained as a lambda term that, when applied, results in the function being applied twice to its argument, illustrating the concept of incrementing a number.
💡Church Numerals
Church numerals are a way of representing natural numbers in lambda calculus, where each numeral is a function. The script discusses how these numerals are defined and used in the lambda calculus, particularly in the context of the successor function and other arithmetic operations like addition and multiplication.
💡Lambda Calculus
Lambda calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application. The video script delves into various aspects of lambda calculus, such as defining numerals and arithmetic operations using lambda expressions.
💡Lambda Expression
A lambda expression is a way to define anonymous functions in lambda calculus. In the script, lambda expressions are used to define the successor function, Church numerals, and other arithmetic operations, showcasing the expressive power of lambda calculus in representing complex operations.
💡Function Application
Function application is the process of applying a function to an argument to produce a result. The script demonstrates function application in the context of the successor function, where the lambda expression is applied to arguments to simulate the incrementing of a number.
💡Meta Language
The term 'meta language' in the script refers to the language used to describe another language, in this case, the language of lambda calculus. The speaker mentions that they are not yet using lambda terminology, indicating a shift to a more formal or specific way of describing the concepts.
💡Programming Language Notation
The script mentions programming language notation when explaining the successor function, drawing a parallel between the lambda calculus approach and more familiar programming concepts, such as incrementing a variable.
💡Arithmetic Operations
Arithmetic operations such as addition, multiplication, and exponentiation are discussed in the script within the framework of lambda calculus. The speaker defines these operations using lambda expressions, showing how they can be represented abstractly without specific numerical values.
💡Plus Function
The plus function in the script is a lambda expression that represents addition in lambda calculus. It's defined in a way that uses the successor function to add two Church numerals, demonstrating how arithmetic can be abstractly represented and computed.
💡Multiplication and Exponentiation
The script briefly touches on the definition of multiplication and exponentiation in lambda calculus. These operations are also defined using lambda expressions, extending the concept of representing arithmetic operations abstractly.
Highlights

Introduction to the successor function in lambda calculus.

Definition of Church numerals and the successor function.

Explanation of how the successor function works with the example of the successor of one.

Description of the lambda notation and its application in defining the successor function.

Illustration of how lambda functions can be used to represent numbers and operations.

Introduction to the concept of lambda calculus and its potential for defining complex functions.

Explanation of how the successor function is applied through lambda notation.

Demonstration of how the successor function can be represented using lambda calculus.

Introduction to the plus function in lambda calculus and its definition.

Explanation of how the plus function is defined and its relation to the successor function.

Introduction to the multiplication function in lambda calculus and its definition.

Explanation of how multiplication is represented in lambda calculus.

Introduction to the power function in lambda calculus and its definition.

Explanation of how powers are represented in lambda calculus.

Discussion on the beauty of lambda calculus in representing mathematical operations.

Promise to show examples of power functions in the next session.

Transcripts

Browse More Related Video

Lambda Calculus Calculator

A Flock of Functions: Combinators, Lambda Calculus, & Church Encodings in JS - Part II

church numerals multipliaction

Add church numerals

PLT: Lambda Calculus - Basics 2 (Church numerals)

lambda calculus review

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Lambda CalculusSuccessor FunctionChurch NumeralsProgramming LogicFunctional ProgrammingMathematical NotationRecursive FunctionsAlgorithm DesignEducational ContentComputer Science