church numerals multipliaction

Evgeniy M
22 Feb 202408:28
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the intricacies of Church numerals and their application in lambda calculus, specifically focusing on multiplication. It explains how multiplication can be represented as repeated addition using Church numerals, with a type signature that encodes two numbers, M and N. The video demonstrates the implementation of a multiplication function in lambda calculus, showcasing the process of partial application and reduction to achieve the desired result. It also touches on the evaluation strategy, namely normal order reduction, which is key to understanding the function's behavior.

Takeaways
  • 📚 The video discusses the encoding of natural numbers using Church numerals in Lambda calculus.
  • 🔢 Church numerals are a way to represent natural numbers as functions in the Lambda calculus.
  • ➕ The script explains how to perform addition with Church numerals using the successor function.
  • 🔄 The multiplication of Church numerals is expressed as repeated addition, a key concept in the video.
  • 📝 The type signature of a Church numeral is provided, which is essential for understanding its function application.
  • 🤔 The multiplication function requires understanding of partial application in Lambda calculus.
  • 🛠️ The script includes an implementation of the multiplication function in Lambda calculus, demonstrating its application.
  • 🔍 The process of reducing the Lambda expressions to compute the result of multiplication is explained.
  • 👨‍🏫 The video uses a step-by-step approach to illustrate the reduction process, aiding in understanding.
  • 🔢 An example is provided where the multiplication of two Church numerals (e.g., 2 and 3) results in 6.
  • 🧠 The importance of understanding the evaluation strategy, specifically normal order reduction, is highlighted.
Q & A

  • What is the main topic discussed in the video?

    -The main topic discussed in the video is how to perform multiplication of Church numerals in Lambda calculus.

  • What are Church numerals?

    -Church numerals are a way of representing natural numbers in Lambda calculus, where each number is represented by a function.

  • How is multiplication of Church numerals represented in Lambda calculus?

    -Multiplication of Church numerals is represented by using the first number to perform the second number's addition to itself repeatedly.

  • What is the type signature mentioned in the script?

    -The type signature represents the arguments for the two numbers M and N in the multiplication function, where M and N are Church numerals.

  • What does the multiplication function do in Lambda calculus?

    -The multiplication function takes two Church numerals, M and N, and returns their product, also encoded as a Church numeral.

  • How is the multiplication function implemented in the video?

    -The multiplication function is implemented by using the first numeral M to perform N additions of itself, effectively applying the function f to N groups of M.

  • What is partial application in the context of the video?

    -Partial application in this context refers to providing some arguments to a function but not all, resulting in a new function that takes the remaining arguments.

  • What is the significance of the reduction process in the multiplication of Church numerals?

    -The reduction process is crucial as it simplifies the expression by applying the functions and performing the necessary substitutions to eventually yield the product as a Church numeral.

  • What is normal order reduction mentioned in the script?

    -Normal order reduction is a strategy in Lambda calculus where the leftmost outmost term is reduced first, followed by the inner terms.

  • How does the video demonstrate the multiplication of two by three using Church numerals?

    -The video demonstrates the multiplication by showing the reduction process that leads to the product of two and three, resulting in six, using the Church numeral representation.

  • What is the final result of the multiplication example given in the video?

    -The final result of the multiplication example (2 by 3) is six, represented as a Church numeral.

Outlines
00:00
📚 Introduction to Church Numerals Multiplication

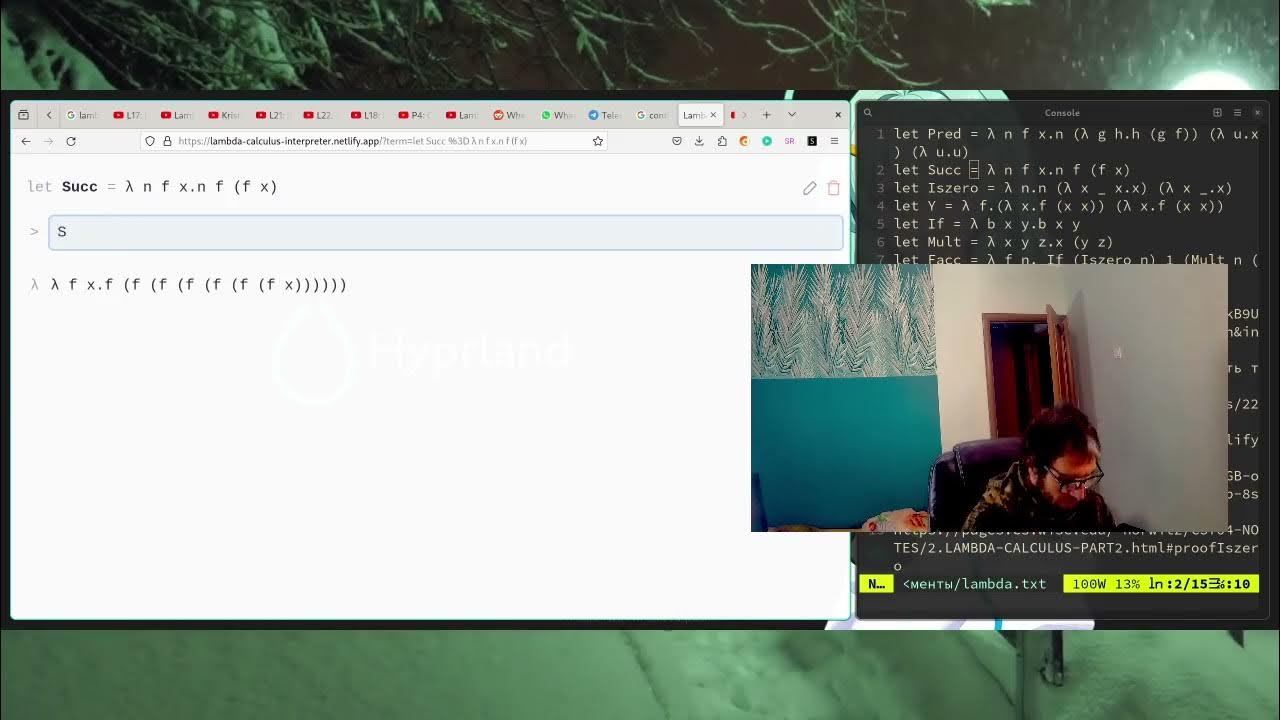
The speaker begins by referencing a previous video where they discussed encoding natural numbers using Church numerals, including the addition operation and successor function. They then introduce the topic of the current video, which is the multiplication of Church numerals. The speaker explains that multiplication can be expressed as repeated addition and that the Church numeral for a number M will be used to perform N additions of M. The process involves a function with a type signature that represents two Church numerals, M and N, and the multiplication of these two numbers. The speaker also mentions the need to understand the Lambda calculus implementation of this multiplication function.

05:01
🔍 Multiplication Function Reduction Process

In this paragraph, the speaker delves into the reduction process of the multiplication function in Lambda calculus. They describe the initial steps of the process, where the Church numerals for three and two are encoded and used as inputs to the multiplication function. The speaker explains the normal order reduction strategy used in the Lambda calculus, which involves choosing the leftmost outmost term for reduction. Through a series of substitutions and applications, the speaker illustrates how the process leads to the correct result of six, which is the product of the two Church numerals. The speaker acknowledges the complexity of the process but emphasizes the main idea of combining groups of N Church numerals M times and then merging them into a single Church numeral.

Mindmap
Keywords
💡Church Numerals
Church Numerals are a way of representing natural numbers in Lambda Calculus using functions. They are named after Alonzo Church, who introduced them. In the video, Church Numerals are used to encode numbers in a functional way. For example, the number 3 is represented as a function that takes another function and an argument and applies the function three times to the argument.
💡Lambda Calculus
Lambda Calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application. It is the foundation of functional programming languages. In the video, Lambda Calculus is used to demonstrate how to encode numbers and perform operations like addition and multiplication using Church Numerals.
💡Multiplication
Multiplication is a fundamental arithmetic operation that combines two numbers to find their product. In the context of the video, multiplication is discussed in relation to Church Numerals, where it is shown how to multiply two Church-encoded numbers using a function that repeatedly applies addition.
💡Addition
Addition is another basic arithmetic operation that sums two or more numbers. The video script mentions addition in the context of how it can be used to express multiplication in Lambda Calculus, specifically through the repeated application of an addition function.
💡Successor Function
The successor function is a function that takes a natural number and returns the next number in the sequence. In Lambda Calculus, the successor function is used to increment Church Numerals. The video script discusses how the successor function can be implemented in Lambda Calculus.
💡Type Signature
A type signature in Lambda Calculus specifies the types of arguments a function can take and the type of value it returns. The video script refers to type signatures in the context of defining functions that operate on Church Numerals, indicating the expected input and output types.
💡Partial Application
Partial application is a concept in Lambda Calculus where a function is applied to some, but not all, of its arguments. The result is a new function that takes the remaining arguments. In the video, partial application is mentioned in the context of defining the multiplication function for Church Numerals.
💡Reduction
Reduction in Lambda Calculus refers to the process of simplifying expressions by applying the rules of the calculus, such as beta reduction, until a normal form is reached. The video script discusses the reduction process in the context of evaluating expressions involving Church Numerals and their operations.
💡Normal Order Reduction
Normal order reduction is a strategy in Lambda Calculus for reducing expressions where the leftmost, outermost redex (reducible expression) is always chosen for reduction. The video script mentions normal order reduction in the context of evaluating the multiplication of Church Numerals.
💡Substitution
Substitution in Lambda Calculus is the process of replacing a variable or an expression with another expression according to the rules of the calculus. The video script refers to substitution in the context of how variables and functions are replaced during the reduction process when evaluating expressions involving Church Numerals.
💡Function Abstraction
Function abstraction is a fundamental concept in Lambda Calculus where a function is defined by a lambda expression that binds a variable to an expression. The video script discusses function abstraction in the context of defining operations like multiplication for Church Numerals.
Highlights

Introduction to encoding natural numbers using Church numerals in Lambda calculus.

Explanation of the Church numerals for non-Church numerals and their encoding.

Discussion on performing addition with Church numerals.

Introduction of the successor function in the context of Church numerals.

Exploration of how to implement multiplication of Church numerals.

Type signature representation for the arguments of two Church numerals M and N.

Multiplication expressed as repeated addition using Church numerals.

Use of M to provide n times addition of N in the multiplication process.

Application of the function f to strip one level of the Lambda signature.

Transformation of n * F into a Lambda function for multiplication.

Description of the cloning process of N groups M times in multiplication.

The need for a multiplication function with partial application.

Signature of Church numerals output for the multiplication function.

Explanation of how to provide the body for the multiplication function.

Multiplication example of two Church numerals to demonstrate the process.

Reduction process leading to the correct multiplication result.

Discussion on the normal order reduction strategy used in the example.

Explanation of the evolution strategy and term selection for reduction.

Substitution process in the Lambda function during multiplication.

Final multiplication result and understanding the evaluation order.

Transcripts

Browse More Related Video

Add church numerals

PLT: Lambda Calculus - Basics 3 (Operations on church numerals)

Lambda Calculus Calculator

A Flock of Functions: Combinators, Lambda Calculus, & Church Encodings in JS - Part II

Lambda Calculus!

lambda calculus reduction strategies

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Lambda CalculusChurch NumeralsMultiplicationFunctional ProgrammingCoding TutorialMathematicsComputer ScienceProgramming ConceptsEducational ContentTechnical Learning