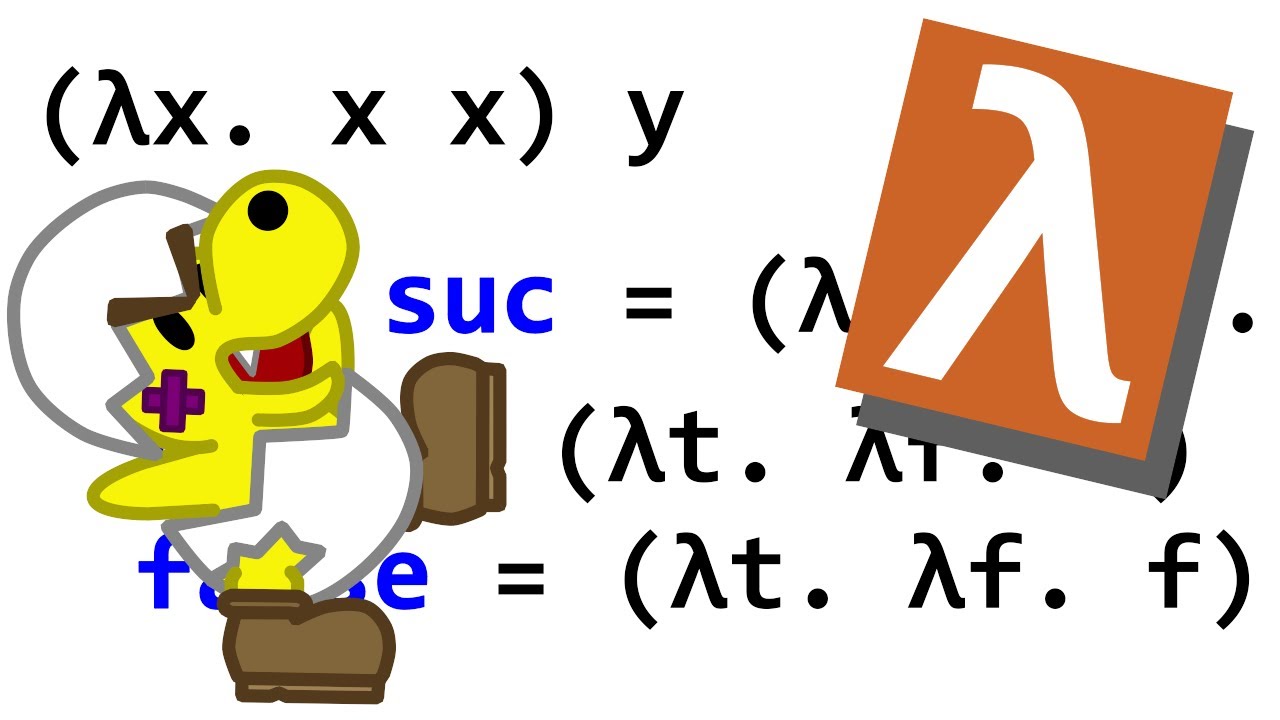Add church numerals
TLDRThe video script discusses Church numerals and their implementation in Lambda calculus for simple calculations like addition. It explains how to add one to a number using Lambda expressions and demonstrates the process with a Lambda calculator, showing how to encode numbers and perform operations like adding two numbers together.
Takeaways
- 😀 Church numerals are used to encode natural numbers in Lambda calculus, which is a formal system for expressing computation.
- 🔢 The plus one function is a basic operation that can be implemented in Lambda calculus by adding one to a given number.
- 📚 Church numerals represent numbers as higher-order functions with two arguments, typically a function and an argument.
- 💡 The plus one function in Lambda calculus involves applying the number to a function and then applying the result to the argument.
- 🔧 The successor function is a Lambda term that takes a number and returns the next number in Church encoding.
- 📈 The plus function in Lambda calculus is defined to take two numbers, M and N, and return their sum.
- 🧩 The process of addition in Lambda calculus involves stripping the Lambda signature from one number and pushing the other number into it.
- 🤔 The Lambda calculator can be used to test and verify the functionality of the plus function and other Church numeral operations.
- 📝 Errors in syntax or spacing can lead to issues in the Lambda calculator, emphasizing the importance of precise input.
- 📚 The script discusses the encoding of numbers and the implementation of basic arithmetic operations like addition in Lambda calculus, highlighting the foundational concepts of functional programming.
Q & A
What are Church numerals in the context of Lambda calculus?
-Church numerals are a way of representing natural numbers in Lambda calculus using lambda expressions. Each numeral is a higher-order function that takes two arguments, a function 'F' and an argument 'X', and encodes the number as a function application.
How can you add one to a Church numeral?
-You can add one to a Church numeral by implementing the successor function. This function takes a Church numeral 'n' as input and applies 'F' to it 'n' times, effectively incrementing the numeral by one.
What is the purpose of the plus one function in Lambda calculus?
-The plus one function is used to increment a given Church numeral by one. It's a fundamental operation that forms the basis for more complex arithmetic operations in Lambda calculus.
How is the successor function represented in Lambda calculus?
-The successor function in Lambda calculus is represented as a lambda term that takes a Church numeral, applies the function 'F' to it, and then applies the result to the argument 'X', effectively creating the next Church numeral in the sequence.
What is the role of the 'F' and 'X' in Church numerals?
-In Church numerals, 'F' is a function and 'X' is an argument. The Church numeral is represented as a function that, when applied 'n' times to 'X', represents the number 'n'.
Can you provide an example of a Church numeral for the number two?
-Yes, the Church numeral for the number two can be represented as a lambda expression that applies 'F' to 'X' twice, often written as 'λfx.FFx'.
What is the process of adding two Church numerals together?
-To add two Church numerals, you use the plus function in Lambda calculus. This function takes two numerals 'M' and 'N', and through a series of function applications, it computes the sum by applying 'F' 'M+N' times to 'X'.
How does the plus function in Lambda calculus work?
-The plus function in Lambda calculus works by taking two Church numerals, stripping the outer lambda from one numeral, and then repeatedly applying 'F' to the result 'N' times, and then 'M' times, effectively computing the sum of 'M' and 'N'.
Can you demonstrate the addition of two Church numerals using a Lambda calculator?
-Yes, by defining the plus function as a Lambda expression and inputting two Church numerals into the calculator, you can see the reduction steps that lead to the Church numeral representing the sum of the two original numerals.
What is the significance of the Lambda calculus in computer science?
-Lambda calculus is significant in computer science as it is the foundation of functional programming languages. It provides a theoretical framework for the manipulation of functions and is used in the study of computation and the design of programming languages.
How can one verify the correctness of the plus function for Church numerals?
-One can verify the correctness of the plus function by testing it with various pairs of Church numerals and observing if the reduction steps lead to the expected results, confirming that the function behaves as intended for addition.
Outlines
📚 Introduction to Church Numerals and Simple Operations
This paragraph introduces the concept of Church numerals, a way to represent natural numbers in Lambda calculus. It discusses how any natural number can be encoded using Lambda terms and how simple calculations, such as adding one to a number, can be implemented. The plus one function is explained as a Lambda expression that takes a number and applies a function to it to achieve the next number in the Church encoding. The paragraph also mentions a Lambda calculus calculator that can be used to test these expressions.
🔢 Utilizing Successor Function with Church Numerals
The second paragraph delves into the practical application of the successor function with Church numerals. It explains how to use the successor function to increment Church numerals and demonstrates this with examples of numerals one and two. The paragraph also highlights a mistake made in encoding the successor function and corrects it, showing the importance of proper Lambda term notation. The process of defining and testing the plus function in a Lambda calculator is also discussed, emphasizing the complexity of the operation.
🤖 Defining and Testing the Plus Function in Lambda Calculus
This paragraph focuses on the encoding and testing of the plus function within Lambda calculus. It explains the process of defining the plus function as a Lambda expression that takes two numbers, M and N, and returns their sum. The paragraph describes the steps involved in the reduction process to achieve the sum and illustrates how to test this function using a Lambda calculator. It also shows examples of adding different pairs of Church numerals to demonstrate the functionality of the plus function.
Mindmap
Keywords
💡Church Numerals
💡Lambda Calculus
💡Plus One Function
💡Function Application
💡Successor Function
💡Lambda Expression
💡Church Encoding
💡Plus Function
💡Lambda Reduction
💡Lambda Calculator
Highlights
Introduction to Church numerals and their encoding in Lambda calculus.
Explanation of how to implement the plus one function in Church numerals.
Demonstration of the process to add one to a Church numeral.
Description of the Lambda term representing a number in Church numerals.
How to apply a function to a Church numeral to achieve the next number.
Introduction to the successor function in Lambda calculus.
Encoding the successor function as a Lambda term.
Using the Lambda calculator to test the successor function with Church numerals.
Problem encountered due to missing spaces in the Lambda expression.
Correcting the Lambda expression to properly encode the successor function.
Testing the successor function with the number one in Church numerals.
Exploring the addition of more complex numbers using the plus function.
Encoding the plus function in Lambda calculus to add two Church numerals.
Detailed explanation of the process to add two numbers using the plus function.
Using the Lambda calculator to define and test the plus function.
Demonstration of adding zero and one using the plus function in Church numerals.
Testing the plus function with larger Church numerals like 2 and 1.
Further testing with larger numbers, such as adding five and three.
Conclusion on the functionality and practicality of the plus function in Church numerals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: