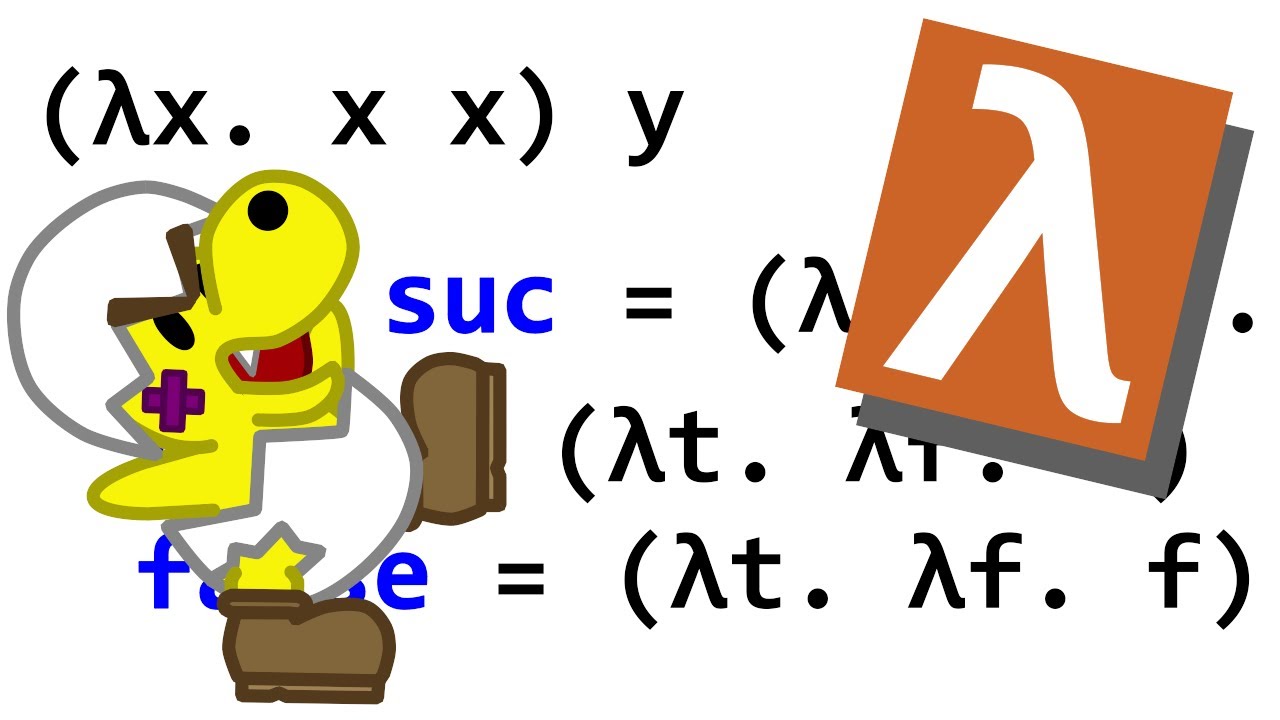PLT: Lambda Calculus - Basics 2 (Church numerals)
TLDRThis script discusses the power of lambda calculus in expressing mathematical problems, focusing on Church numerals for representing numbers. It explains how numbers can be defined in lambda calculus, using functions like successor to build up from zero. The speaker emphasizes the importance of defining functions correctly to maintain mathematical rules.
Takeaways
- 🧠 Lambda calculus is a powerful system that can express any mathematical problem.
- 🔢 Mathematical operators and numbers can be mapped into pure lambda calculus notation.
- 📚 Lambda calculus is primarily used for expressing mathematical computations, not for concurrency or multi-threading.
- 👨🏫 Church numerals, named after Alonzo Church, are a common system for defining numbers in lambda calculus.
- 🎯 Church defined zero as a lambda function that takes a parameter F and returns X, representing the absence of repeated application.
- 🔑 The number one is represented by a lambda function that applies F to X once, essentially doubling X.
- 🔢 Higher numbers like two or three are represented by repeatedly applying the function F to X, following a pattern.
- 💡 The choice of how to represent numbers in lambda calculus is arbitrary but must obey mathematical rules.
- 🔄 Functions that act on numbers in lambda calculus must be defined to work with these number representations.
- 🔗 The successor function in lambda calculus is defined as a lambda function that takes a number n and returns a new function that applies F to X n times.
Q & A
What is lambda calculus?
-Lambda calculus is a formal system in mathematical logic and computer science for expressing computation by way of function abstraction and application using variable binding and substitution.
Why is lambda calculus considered the ultimate system for expressing any mathematical problem?
-Lambda calculus is considered ultimate because it can express any computation or mathematical problem through its basic operations of function abstraction and application, without the need for numbers or arithmetic operators as they are defined in traditional mathematics.
What are Church numerals?
-Church numerals are a way of representing natural numbers in lambda calculus, invented by Alonzo Church. They are defined using lambda functions and enable the encoding of arithmetic operations within the lambda calculus framework.
How is the number zero represented in Church numerals?
-In Church numerals, zero is represented as a lambda function that takes a function 'F' and an argument 'X' and simply returns 'X', effectively ignoring the function 'F'.
Can you provide an example of how the number one is represented in Church numerals?
-The number one is represented as a lambda function that takes 'F' and 'X', and applies 'F' to 'X' once, which can be written as λFX.F X.
What is the purpose of defining numbers in lambda calculus?
-Defining numbers in lambda calculus allows for the encoding of arithmetic operations and mathematical computations within the framework of lambda calculus, which only natively supports functions and variables.
What is the role of the successor function in the context of Church numerals?
-The successor function in Church numerals takes a number and returns the next number in the sequence. It is defined as a lambda function that applies its argument 'n' to 'F' and 'X', effectively incrementing the numeral by one.
How does lambda calculus differ from process calculi in terms of expressing concurrency?
-While lambda calculus is capable of expressing all mathematical computations, it does not inherently express concepts like multi-threading and concurrency. Process calculi, on the other hand, are specifically designed to model concurrent systems and interactions.
What is the significance of the lambda abstraction notation in representing computations?
-Lambda abstraction notation is significant because it allows for the representation of functions as first-class citizens, enabling the expression of complex computations through function application and composition.
Can lambda calculus represent all possible computations?
-Yes, lambda calculus is a Turing-complete system, meaning it can represent any computation that can be performed by a Turing machine, which is considered the theoretical basis for computability.
What are the limitations of using lambda calculus for practical programming?
-While lambda calculus is a powerful theoretical framework, its direct use in practical programming can be limited due to its abstract nature and lack of built-in data structures and control structures that are common in modern programming languages.
Outlines
🧠 Introduction to Lambda Calculus and Church Numerals
This paragraph introduces the concept of lambda calculus, emphasizing its ability to express any mathematical problem. The speaker clarifies that while lambda calculus can represent arithmetic operations and numbers, it does not inherently handle multi-threading or concurrency, which are managed by process calculi. The focus then shifts to defining numbers within lambda calculus, specifically mentioning Church numerals. Church numerals are a method of representing numbers using lambda functions, with zero defined as a function that ignores the argument and returns it, and each subsequent number defined as an application of the function to itself a corresponding number of times.
🔢 Defining Numbers and Successor Function in Lambda Calculus
The second paragraph delves deeper into the representation of numbers in lambda calculus, using the Church numerals system. It explains the process of defining a successor function, which is essential for creating arithmetic operations within lambda calculus. The successor function is defined as a lambda term that takes a number 'n' and returns a function that, when applied to an argument 'X', results in 'n' being applied to 'X' one additional time. This paragraph also touches on the complexity of lambda calculus syntax and the importance of defining functions that correctly operate on these numeral representations.
Mindmap
Keywords
💡Lambda Calculus
💡Church Numerals
💡Lambda Abstraction
💡Function Application
💡Successor Function
💡Multi-threading and Concurrency
💡Numerics System
💡Lambda Term
💡Syntax
💡Computational Universality
💡Functional Programming
Highlights
Lambda calculus can express any mathematical problem.
Lambda calculus does not inherently include arithmetic operators or numbers.
All arithmetic operators and numbers can be mapped into pure lambda calculus notation.
Lambda calculus expresses all mathematical computations but does not handle multi-threading or concurrency.
Process calculi are used for handling concurrency, but not discussed in this context.
Numbers in lambda calculus are defined using lambda syntax and variables.
Church numerals are a commonly used system for defining numbers in lambda calculus.
Church numerals were defined by Alonzo Church, the inventor of lambda calculus.
Zero is defined as a lambda function that returns its argument X without applying any function.
The number one is represented by a function that applies its argument once.
The number two is represented by a function that applies its argument twice.
The pattern continues with each number represented by a function that applies its argument that number of times.
The choice of representation for numbers in lambda calculus is arbitrary but must obey mathematical rules.
Functions that act on numbers in lambda calculus must be defined to work with these number definitions.
Basic operations will be demonstrated to show that these number definitions work as intended.
The successor function is defined in lambda calculus as a function that takes a number and returns the next number.
The successor function is represented as a lambda term with three parameters.
Lambda calculus syntax can be confusing, but the transcription attempts to clarify the notation used.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: