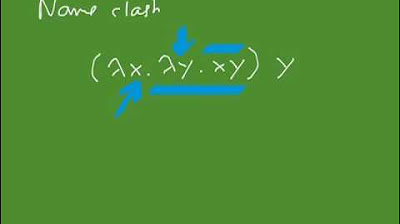lambda calculus review
TLDRThe video script delves into the Lambda calculus, a formal system foundational to computation, emphasizing its three core rules for constructing valid terms. It highlights the absence of variable declarations, the concept of function as a first-class value, and the importance of alpha equivalence and beta reduction in computation steps. The script also touches on untyped Lambda calculus, its relation to functional programming, and introduces combinators and Church numerals, concluding with a mention of typed Lambda calculus and its variants.
Takeaways
- 📚 Lambda calculus is a formal system designed to express computation, based on concepts like abstraction, application, and variable binding.
- 🔡 It has an alphabet and syntax that define valid Lambda terms through free induction rules, with three fundamental rules for term construction.
- 🆔 Variables in Lambda calculus are valid terms by themselves, and abstractions represent anonymous functions with a single argument.
- 🔗 Application in Lambda calculus is the process of applying a function to an argument, creating a new term.
- 🈚️ Unlike imperative languages, Lambda calculus does not require variable declarations; it uses arguments for functions.
- 🔄 Functions in Lambda calculus are first-class values, meaning they can be passed around and returned from other functions.
- 🔄 Function composition is demonstrated through a simple Lambda term that applies one function to another, showcasing the concept.
- 🔄 Alpha equivalence in Lambda calculus allows for variable renaming under abstraction to determine if two terms are equivalent.
- 🔄 Beta reduction is the main computation step in Lambda calculus, involving substitution of bound variables with other terms.
- 🔢 Church numerals are a way to encode numbers in Lambda calculus, using the number of function applications to an argument.
- 🔧 Lambda calculus can be seen as an abstracted version of functional programming languages, where computation involves step-by-step beta reduction.
- 🔒 Untyped Lambda calculus does not distinguish between different kinds of data, which can lead to non-termination if not handled properly.
- 🔄 Normal forms in Lambda calculus are terms that cannot be reduced further, representing the end of computation.
- 🔄 Combinators are terms with no free variables, representing fundamental operations in Lambda calculus.
- 🔄 Lambda calculus supports parallel evaluation of terms, as the order of evaluation does not affect the outcome.
- 📚 There are many variations and extensions of Lambda calculus, including typed Lambda calculus and system F, which introduce types to variables and functions.
Q & A
What is Lambda calculus?
-Lambda calculus is a formal system for expressing the notion of computation. It is based on concepts such as abstractions, applications, variable binding, and substitutions. It can simulate any Turing machine, making it a powerful tool in theoretical computer science.
What are the basic components of Lambda calculus syntax?
-The syntax of Lambda calculus can be defined using free inductive rules. It includes variables, abstractions (which represent anonymous functions), and applications (which represent the application of a function to an argument).
How are valid Lambda terms constructed?
-Valid Lambda terms are constructed by repeatedly applying three rules: 1) any variable is a valid Lambda term, 2) if T is a Lambda term and X is a variable, then \( \lambda X.T \) (abstraction) is also a valid Lambda term, and 3) if T and S are Lambda terms, then \( (T\ S) \) (application) is also a valid Lambda term.
What is the significance of variable declarations in Lambda calculus?
-In Lambda calculus, there is no concept of variable declarations as in imperative languages. Instead, variables are bound within the scope of Lambda abstractions and can be free variables if they are not bound.
How does Lambda calculus treat functions?
-In Lambda calculus, functions are first-class values. This means that functions can be passed as arguments to other functions and can return new functions, allowing for function composition and higher-order functions.
What is the concept of alpha equivalence in Lambda calculus?
-Alpha equivalence is a form of equivalence in Lambda calculus where two terms are considered equivalent if they can be obtained by renaming the bound variables under Lambda abstractions and result in the same term.
What is beta reduction in Lambda calculus?
-Beta reduction is the main computation step in Lambda calculus. It involves substituting the bound variable in a Lambda expression with another term and performing this substitution everywhere in the expression body.
How does Lambda calculus relate to function programming languages?
-Lambda calculus can be seen as an idealized version of function programming languages. Languages like Haskell use some form of Lambda calculus under the hood, performing beta reduction steps during computation.
What is the issue with untyped Lambda calculus?
-Untyped Lambda calculus does not distinguish between different kinds of data. This lack of type system can lead to situations where functions are applied to inappropriate data types, potentially causing non-terminating computations.
What are combinators in Lambda calculus?
-Combinators in Lambda calculus are terms that have no free variables; they only contain bound variables. They are fundamental building blocks in the system, such as the identity combinator and SK combinators.
How does Lambda calculus handle parallelism?
-Lambda calculus does not offer explicit constructs for parallelism. However, its nature allows for the evaluation of terms in different orders without affecting the outcome, which can be leveraged for implicit parallelization.
What are some variations and extensions of Lambda calculus?
-There are many variations and extensions of Lambda calculus, such as typed Lambda calculus, which adds a type system, and system F, which is a polymorphic type system. These variations aim to address limitations and extend the capabilities of the original untyped Lambda calculus.
Outlines
📘 Introduction to Lambda Calculus
The first paragraph introduces the Lambda calculus as a formal system for expressing computation. It emphasizes the foundational concepts of abstraction, application, and variable binding and substitution. The Lambda calculus is described as a language with its own syntax, defined by inductive rules that create valid Lambda terms. The rules include variables as terms, abstractions representing anonymous functions, and applications of these functions. The paragraph also touches on the absence of variable declarations and the concept of function as a first-class value, which can be passed around and returned from other functions. The notion of alpha equivalence is introduced, which allows for variable renaming under abstractions to achieve equivalent terms.
🔍 Beta Reduction and Computation in Lambda Calculus
The second paragraph delves into the concept of beta reduction, which is central to the computational steps in Lambda calculus. It explains how substitution of bound variables with other terms is performed, leading to the removal of the instruction path before the dot, representing a single computation step. The paragraph also discusses the idea of a computation being complete when no further reduction steps can be applied, and the potential for infinite reductions leading to non-termination. It contrasts untyped Lambda calculus, which does not distinguish between different kinds of data, with typed Lambda calculus that introduces types to variables and functions to avoid certain issues. The paragraph concludes with the notion of normal forms in computation, where terms that can be reduced are called reducibles, and those that cannot be further reduced are called normal forms.
🔢 Church Numerals and Combinators in Lambda Calculus
The third paragraph explores the encoding of numbers in Lambda calculus through Church numerals, which represent numbers as repeated applications of functions. It also introduces combinators, terms with no free variables that are bound, serving as standard building blocks in the calculus. The paragraph highlights the ability to evaluate Lambda terms in different orders without affecting the result, indicating the potential for parallel evaluation. It also mentions the lack of explicit constructs for parallelism in Lambda calculus but notes the existence of formal systems like process calculus that describe communication and concurrency. The paragraph concludes with a brief mention of various types of Lambda calculus, including typed and system F, and other variations that extend the basic framework.
Mindmap
Keywords
💡Lambda calculus
💡Abstraction
💡Application
💡Variable binding
💡Substitution
💡First-class value
💡Alpha equivalence
💡Beta reduction
💡Normal form
💡Church numerals
💡Combinators
💡Type theory
Highlights
Lambda calculus is a formal system for expressing computation based on concepts like abstractions, applications, variable binding, and substitutions.
Lambda calculus can simulate any Turing machine, demonstrating its computational completeness.
The syntax of Lambda calculus is defined using free inductive rules, leading to the definition of valid Lambda terms.
Variables themselves are valid Lambda terms, as per the first rule of Lambda calculus syntax.
Abstraction is represented by 'λ', indicating an anonymous function with a single argument.
Application in Lambda calculus is represented by function application to an argument, a key part of computation steps.
Lambda terms are valid if they can be obtained by applying the three syntactic rules iteratively.
There is no concept of variable declarations in Lambda calculus, unlike imperative languages.
Functions in Lambda calculus are first-class values, meaning they can be treated like any other data type.
Function composition in Lambda calculus can be defined using simple term structures.
Alpha equivalence in Lambda calculus allows for variable renaming under lambda abstraction to determine term equivalence.
Beta reduction is the primary computation step in Lambda calculus, involving substitution of bound variables.
Lambda calculus can be seen as an abstracted version of functional programming languages, with underlying mechanisms similar to those in Haskell or Lisp.
The concept of normal form in Lambda calculus represents the final point of computation where no further reduction steps can be made.
Untyped Lambda calculus does not distinguish between different kinds of data, unlike typed Lambda calculus variants.
Church numerals are an example of how numbers can be encoded within Lambda calculus using function applications.
Combinators in Lambda calculus are terms with no free variables, playing a significant role in the system.
Lambda calculus supports parallel evaluation of terms, allowing for implicit parallelization of computations.
There are many variations and extensions of Lambda calculus, each with unique properties and applications.
Lambda calculus lacks explicit constructs for parallelism, unlike formal systems like process calculus designed for concurrency.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: