Lec 2: Determinants; cross product | MIT 18.02 Multivariable Calculus, Fall 2007

MIT OpenCourseWare

16 Jan 200952:51

EducationalLearning

32 Likes 10 Comments

TLDRThis video script covers fundamental vector operations, focusing on the dot product and its applications, such as finding vector lengths, angles, and detecting perpendicularity. It introduces the concept of vector components along a direction and their physical applications, like analyzing forces on a pendulum. The script then delves into the determinant's role in calculating areas and volumes, especially in the context of triangles, parallelograms, and parallelepipeds. Finally, it explains the cross product for three-dimensional vectors, highlighting its use in determining the area of parallelograms and the volume of parallelepipeds, along with the right-hand rule for direction.

Takeaways

📚 The script is from a lecture on vector operations, discussing the dot product and its applications in finding lengths, angles, and components of vectors.
🔍 The dot product is defined as the sum of the products of the corresponding components of two vectors, resulting in a scalar.
📐 The geometric interpretation of the dot product involves the lengths of the vectors and the cosine of the angle between them.
⚖️ An application of the dot product is determining the cosine of the angle between two vectors, using the formula cosine(theta) = dot product / (length of a * length of b).
🧭 Another application is checking for perpendicularity between vectors; if the dot product is zero, the vectors are perpendicular.
📈 The dot product can also be used to find the component of a vector 'a' along a given direction 'U', which is the projection of 'a' onto 'U'.
📚 The script also covers the concept of area in vector mathematics, specifically how to calculate the area of a triangle using vectors.
📏 The area of a triangle can be found using the determinant of two vectors, which is equivalent to the absolute value of the cross product of the vectors.
📉 The determinant of vectors in a 2D plane measures the area of the parallelogram formed by the vectors, and the area of the triangle is half of that.
📊 The script introduces the concept of the cross product for vectors in 3D space, which results in a vector perpendicular to the plane formed by the original vectors.
📘 The cross product's length represents the area of the parallelogram defined by the two original vectors, and its direction is determined by the right-hand rule.

Q & A

What is the definition of the dot product of two vectors?
-The dot product of two vectors is obtained by multiplying the corresponding components of the vectors and summing these products, resulting in a scalar value. It can also be interpreted geometrically as the product of the magnitudes of the two vectors and the cosine of the angle between them.
How can the dot product be used to find the cosine of the angle between two vectors?
-The cosine of the angle between two vectors can be found by dividing their dot product by the product of their magnitudes.
What is one way to determine if two vectors are perpendicular using the dot product?
-To determine if two vectors are perpendicular, compute their dot product. If the result is zero, the vectors are perpendicular.
How can the dot product be used to find the component of a vector along a given direction?
-The component of a vector 'a' along a unit vector 'u' can be found using the dot product of 'a' and 'u'. This is because the dot product gives the product of the magnitudes of the two vectors and the cosine of the angle between them, which is equivalent to the component length when 'u' is a unit vector.
What is the geometric interpretation of the determinant of two vectors?
-The determinant of two vectors geometrically represents twice the area of the parallelogram formed by the vectors. It can be positive or negative, depending on the orientation of the vectors.
How can you find the area of a triangle using vectors?
-The area of a triangle can be found by taking the absolute value of the determinant of two vectors that represent two sides of the triangle and then dividing by two.
What is the relationship between the cross product and the area of a parallelogram in three-dimensional space?
-The magnitude of the cross product of two vectors in three-dimensional space is equal to the area of the parallelogram formed by those vectors.
What does the direction of the cross product vector represent in three-dimensional space?
-The direction of the cross product vector is perpendicular to the plane formed by the original two vectors, following the right-hand rule for determining the direction.
How can you find the volume of a parallelepiped formed by three vectors?
-The volume of a parallelepiped formed by three vectors can be found by taking the absolute value of the determinant of the three vectors.
What is the triple product, and how is it related to the volume of a parallelepiped?
-The triple product is the result of a dot product of one vector with the cross product of the other two vectors. It is equal to the determinant of the three vectors and represents the volume of the parallelepiped formed by these vectors.

Outlines

00:00

📚 Introduction to Dot Product and Vector Operations

This paragraph introduces the concept of the dot product and its applications in vector operations. The dot product is defined as the sum of the products of the corresponding components of two vectors, resulting in a scalar. It has a geometric interpretation involving the lengths of the vectors and the cosine of the angle between them. The paragraph discusses how the dot product can be used to find the cosine of the angle between two vectors, determine if they are perpendicular, and calculate the component of a vector along a given direction. It also explains how to find the component along a unit vector by using the dot product.

05:01

🔍 Applications of Dot Product in Physics

The second paragraph explores the use of dot products in physics, specifically in analyzing the motion of a pendulum. It discusses how to break down the forces acting on a pendulum—such as weight and tension—into components along tangential and normal unit vectors to the trajectory of the pendulum. These components are crucial for understanding the pendulum's motion and the tension in the string. The paragraph emphasizes the utility of vector components in solving physics problems involving motion and forces.

10:02

📐 Vectors and the Area of Polygons

This paragraph delves into the application of vectors to calculate the area of polygons, starting with triangles as the fundamental shape. It explains that the area of a triangle can be found using the lengths of two sides and the sine of the included angle, which is related to the dot product. The paragraph introduces the concept of rotating a vector by 90 degrees to find the area of a triangle using the determinant of two vectors, which simplifies to the cross product of their components. This method is an alternative to using trigonometric functions to find the area.

15:03

🔄 Rotation of Vectors and Area Calculation

The fourth paragraph continues the discussion on calculating the area of a triangle using vectors. It explains the process of rotating a vector by 90 degrees to form a new vector, which is then used in conjunction with the original vector to find the area. The rotation is achieved by changing the signs of certain components, resulting in a new vector that, when dotted with the original, yields the area of the triangle. This approach is a precursor to the determinant method for calculating areas.

20:12

📏 Determinants and the Area of Parallelograms

This paragraph introduces the concept of determinants as a means to calculate the area of parallelograms formed by two vectors. It explains that the determinant, which is computed from the components of the vectors, gives the area of the parallelogram directly. The paragraph also discusses the geometric interpretation of the determinant, noting that it can be positive or negative depending on the orientation of the vectors, and emphasizes the importance of taking the absolute value to obtain the actual area.

25:12

📦 Determinants in Three Dimensions

The sixth paragraph extends the concept of determinants to three dimensions, showing how they can be used to calculate the volume of a parallelepiped formed by three vectors. It explains the formula for the 3x3 determinant and how it relates to the volume of the parallelepiped. The paragraph also touches on the importance of the negative sign in the determinant formula, which is crucial for accurately determining the volume.

30:13

🤔 Cross Product and Vector Perpendicularity

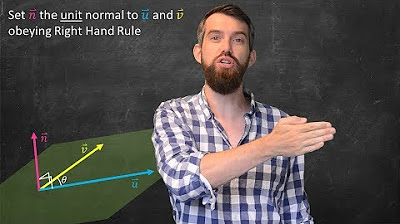
The seventh paragraph introduces the cross product, a vector operation unique to three-dimensional space. It explains that the cross product of two vectors results in a new vector that is perpendicular to the plane containing the original vectors. The length of this new vector is equal to the area of the parallelogram formed by the original vectors, and its direction is determined by the right-hand rule. The cross product is a fundamental tool for understanding the geometry of 3D space.

35:17

👐 Right-Hand Rule and Cross Product Direction

This paragraph provides a practical explanation of the right-hand rule, which is used to determine the direction of the cross product of two vectors. It describes the physical motion of the hand to visualize the direction of the resulting vector and provides an example using the unit vectors i and j to demonstrate the calculation and the right-hand rule in action.

40:17

📐 Cross Product Calculation and Geometric Interpretation

The ninth paragraph continues the discussion on the cross product, focusing on its calculation using determinants and the geometric interpretation of the result. It explains how to compute the cross product of two vectors and emphasizes the importance of the determinant in finding the area of the parallelogram formed by the vectors. The paragraph also reiterates the perpendicular nature of the cross product vector to the plane of the original vectors.

45:20

📊 Volume Calculation Using Cross Product and Dot Product

The final paragraph ties together the concepts of the cross product and dot product to calculate the volume of a parallelepiped. It explains that the volume can be found by taking the dot product of one vector with the cross product of the other two. The paragraph concludes with a geometric interpretation of the determinant as the triple product, which equals the volume of the parallelepiped, and notes that the order of operations is crucial in these calculations.

Mindmap

Keywords

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two equal-length sequences of numbers and returns a single number. In the context of the video, the dot product of two vectors is calculated by multiplying corresponding components and summing these products, resulting in a scalar. It is used to find the cosine of the angle between two vectors and to determine if vectors are perpendicular. For example, the script mentions using the dot product to find the cosine of the angle between two vectors by dividing the dot product by the product of their magnitudes.

💡Vector Components

Vector components refer to the individual elements of a vector, typically in a coordinate system. In the video, the concept is used to explain how to find the component of a vector along a given direction or unit vector. The script discusses finding the component of vector 'a' along direction 'U' by using the dot product of 'a' with 'U', which is particularly useful in physics for analyzing forces in different directions.

💡Unit Vector

A unit vector is a vector that has a magnitude (or length) of one and is commonly used to specify direction in a coordinate system. In the script, unit vectors are mentioned in the context of finding the component of a vector along a certain direction. For instance, to find the component along the x-axis (I hat), one would use the dot product with the unit vector along that axis.

💡Cross Product

The cross product is an operation on two vectors in three-dimensional space, resulting in a vector that is perpendicular to the plane containing the two original vectors. The script introduces the cross product as a means to find the area of a parallelogram formed by two vectors and also to determine the direction perpendicular to their plane. The right-hand rule is mentioned for determining the direction of the resulting vector.

💡Determinant

In mathematics, a determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix. In the video, determinants are used to find the area of a parallelogram and the volume of a parallelepiped. The script explains how the determinant of two vectors in a 2x2 matrix gives the area of the parallelogram they form, and the determinant of three vectors in a 3x3 matrix gives the volume of the parallelepiped they form.

💡Parallelepiped

A parallelepiped is a three-dimensional figure formed by six parallelograms. In the context of the video, the volume of a parallelepiped is discussed in relation to the determinant of three vectors that define its sides. The script explains that the determinant of these vectors equals the volume of the parallelepiped, which is a key concept in understanding how to calculate volumes in three-dimensional space.

💡Right-Hand Rule

The right-hand rule is a common mnemonic for understanding the direction of the cross product of two vectors. The script describes the right-hand rule as a method to determine the direction of the vector resulting from the cross product. By pointing the right hand in the direction of the first vector and curling the fingers towards the second vector, the thumb points in the direction of the cross product.

💡Tangent Vector

A tangent vector is a vector that is tangent to a curve or surface at a given point. In the script, the concept of a tangent vector is introduced in the context of analyzing the motion of a pendulum. The tangent vector 't' is used to describe the direction of motion along the trajectory of the pendulum, which is crucial for understanding the forces acting on the pendulum.

💡Normal Vector

A normal vector is a vector that is perpendicular to a surface or curve at a given point. The script mentions the normal vector 'n' in the context of the pendulum example, where it is used to describe the direction perpendicular to the trajectory of the pendulum. This is important for analyzing the component of the weight that contributes to the tension in the string.

💡Triple Product

The triple product is a mathematical operation involving three vectors, often represented as the scalar triple product. In the video, the triple product is discussed in the context of finding the volume of a parallelepiped using the dot product of one vector with the cross product of the other two. The script explains that the determinant of three vectors is equivalent to the triple product, which is a fundamental concept in vector calculus.

Highlights

Introduction to vector operations and the dot product, emphasizing its definition and geometric interpretation.

Explanation of how the dot product can be used to find the cosine of the angle between two vectors.

Application of the dot product to determine if two vectors are perpendicular by checking if their dot product equals zero.

Discussion on finding the component of a vector along a given direction using the dot product.

Illustration of how to calculate the component of a vector along the x-axis or z-axis using unit vectors.

Introduction of the concept of using vectors to analyze physical phenomena, such as the forces on a swinging pendulum.

Introduction to the concept of area in vector mathematics and the simplification to triangles for computation.

Explanation of how to calculate the area of a triangle using vectors and the sine of the angle between them.

Introduction to the determinant as a method to find the area of a parallelogram formed by two vectors.

Clarification on the sign of the determinant and its relation to the orientation of the vectors.

Transition to three-dimensional space and the concept of determinants for volume calculation.

Definition and explanation of the 3x3 determinant for volume calculation in three-dimensional space.

Discussion on the geometric interpretation of the determinant of three vectors as the volume of a parallelepiped.

Introduction to the cross product as a vector operation unique to three-dimensional space.

Explanation of the geometric meaning of the cross product, including its magnitude as the area of the parallelogram formed by two vectors.

Description of the direction of the cross product as perpendicular to the plane formed by the original vectors, using the right-hand rule.

Example calculation of the cross product of unit vectors i and j, resulting in the unit vector k.

Connection between the determinant of three vectors and the triple product, illustrating an alternative method for volume calculation.

Conclusion of the lecture with a preview of upcoming topics, including matrices and equations of planes.

Transcripts

Browse More Related Video

Calculus 3: The Cross Product (Video #4) | Math with Professor V

Geometrically Defining the Cross Product | Multivariable Calculus

Calculus 3: The Dot Product (Video #3) | Math with Professor V

Ch. 9.5 The Cross Product

Cross Product and Dot Product: Visual explanation

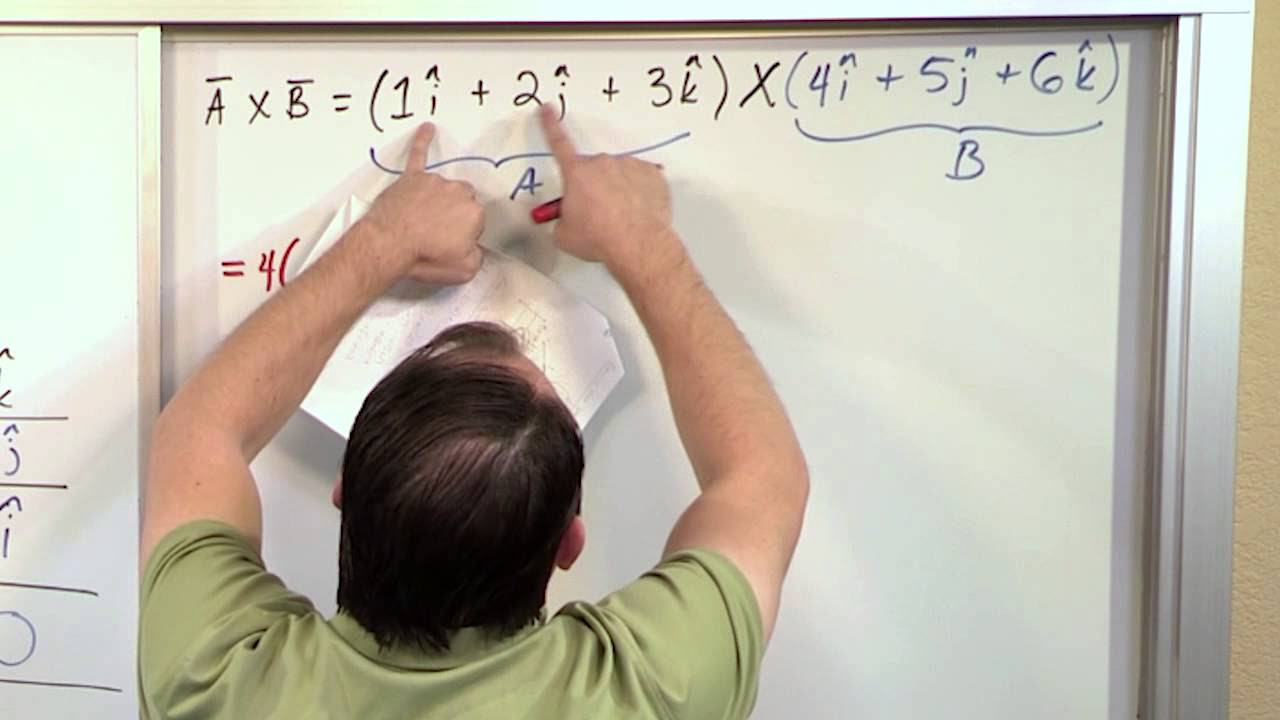
How to Calculate the Vector Cross Product

Related Tags

Vector Operations Dot Product Cross Product MIT Courses Physics Mechanics Educational Resources Mathematics Tutorial Parallelogram Area Determinants 3D Geometry Pendulum Motion