Ch. 9.5 The Cross Product

Prof. Williams

17 Apr 202230:12

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture delves into the concept of the cross product, a mathematical operation that combines two vectors to produce a new vector with unique properties. It introduces the determinant as a preliminary concept, crucial for understanding the cross product, particularly in the context of 2x2 and 3x3 matrices. The script explains the process of finding the determinant, the right-hand rule for orientation, and the geometric interpretation of the cross product as the area of a parallelogram formed by two vectors. It also touches on the scalar triple product and its relation to the volume of a parallelepiped, offering a comprehensive exploration of vector operations.

Takeaways

📚 The lesson discusses Chapter 9.5, focusing on the concept of the cross product in vector mathematics.
🔍 The cross product is a method to multiply two vectors resulting in a new vector, unlike the dot product which results in a scalar.
📏 The determinant is introduced as a prerequisite for understanding the cross product, with a deeper discussion planned for Chapter 10.
📈 The determinant of a 2x2 matrix is calculated using the elements of two vectors arranged in a matrix, with the cross product being an application of this concept.
📐 For a 3x3 matrix, the determinant is found by breaking it down into a series of 2x2 determinants, using an alternating sum method.
🤔 The cross product is defined by a formula involving unit vectors i, j, and k, and is calculated using a determinant with these unit vectors and the components of the two vectors involved.
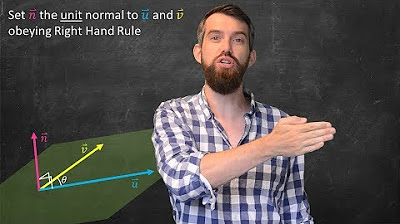
⊥ The resulting vector from the cross product is orthogonal (perpendicular) to both of the original vectors, lying in a direction determined by the right-hand rule.
🤲 The right-hand rule is a method to visualize the direction of the cross product, where the thumb points in the direction of the cross product when the fingers represent the two original vectors.
📏 The magnitude of the cross product is equal to the product of the magnitudes of the two vectors and the sine of the angle between them, representing the area of the parallelogram formed by the vectors.
🤹 The scalar triple product is a combination of the cross and dot products, involving three vectors, and can be used to determine if vectors are coplanar or to calculate the volume of a parallelepiped.
📊 The scalar triple product can be calculated either by finding the determinant of a 3x3 matrix or by using the geometric interpretation involving the lengths of the vectors and the angle between them.

Q & A

What is the cross product of two vectors?
-The cross product of two vectors is a mathematical operation that results in a new vector that is orthogonal to the original two vectors. It is a binary operation in three-dimensional space, and it has special properties related to the vectors it is derived from.
How is the determinant related to the cross product?
-The determinant is used to calculate the cross product in a formulaic way. For a 2x2 matrix, the determinant is the difference between the products of the elements of the main and secondary diagonals. For the cross product, the determinant of a matrix with unit vectors i, j, k and the two vectors to be crossed is used.
What is the significance of the right-hand rule in the context of the cross product?
-The right-hand rule is a common mnemonic for understanding the direction of the cross product. By aligning the fingers of the right hand to represent the two vectors and pointing the thumb in the direction of the cross product, one can determine the direction of the resulting vector.
How does the cross product relate to the concept of torque in physics?
-The cross product is directly related to torque in physics. Torque is the rotational equivalent of force, and it can be calculated as the cross product of the radius vector and the force vector acting at a point.
What is the scalar triple product and how is it related to the cross product?
-The scalar triple product is the result of taking the dot product of one vector with the cross product of two other vectors. It is a scalar value that can be used to determine the volume of a parallelepiped formed by the three vectors.
What does it mean for two vectors to be orthogonal?
-Two vectors are orthogonal if they are perpendicular to each other, forming a right angle. In the context of the cross product, the resulting vector is orthogonal to both of the original vectors.
How can you determine if three vectors are coplanar using the scalar triple product?
-If the scalar triple product of three vectors is zero, it indicates that the vectors are coplanar, meaning they all lie in the same plane.
What is the geometric interpretation of the scalar triple product?
-The absolute value of the scalar triple product represents the volume of a parallelepiped formed by the three vectors. It can be calculated as the area of the base (formed by the cross product of two vectors) multiplied by the height (given by the dot product of the third vector with the normal vector of the base).
How is the area of a parallelogram related to the cross product of two vectors?
-The magnitude of the cross product of two vectors is equal to the area of the parallelogram formed by the vectors. It is calculated as the product of the magnitudes of the two vectors and the sine of the angle between them.
What happens to the cross product if the two vectors are parallel?
-If two vectors are parallel, their cross product is the zero vector. This is because there is no unique direction orthogonal to both vectors when they are parallel.

Outlines

00:00

📚 Introduction to the Cross Product and Determinant

The script begins with an introduction to Chapter 9.5, focusing on the cross product, a mathematical operation that combines two vectors to produce a new vector with unique properties. The instructor contrasts the cross product with the dot product, which yields a scalar value. The determinant, a concept to be explored in depth in Chapter 10, is introduced as a preliminary concept for understanding the cross product. The explanation includes a practical approach to visualizing vectors in R2 as elements of a matrix, emphasizing the importance of rows and columns in matrix formation and the concept of a square matrix necessary for determinant calculation.

05:01

🔍 Deep Dive into Determinants and 3x3 Matrices

The script continues with an in-depth look at how to calculate the determinant of a 2x2 matrix and extends the explanation to 3x3 matrices. The instructor describes the process of finding sub-determinants within a larger matrix and introduces a mnemonic technique for remembering the alternating signs and coefficients involved in the calculation. The determinant is clarified as a scalar value resulting from matrix multiplication and subtraction, not a vector, and the script provides a step-by-step method for calculating it.

10:02

📐 The Cross Product Formula and Its Geometric Interpretation

This paragraph delves into the specifics of the cross product formula in three dimensions, explaining how to use unit vectors i, j, and k with the components of two given vectors to compute a new vector. The formula is presented in a step-by-step manner, illustrating how to arrange the vectors and unit vectors to calculate the cross product. The resulting vector is described as orthogonal to both original vectors, highlighting the geometric significance of the cross product in three-dimensional space.

15:02

🤔 Orthogonality and the Right-Hand Rule for Cross Products

The script discusses the orthogonality of the cross product, explaining that the resulting vector is perpendicular to the original vectors involved in the multiplication. It introduces the right-hand rule as a method to visualize and understand the direction of the cross product. The instructor uses the analogy of the right hand to describe how the cross product relates to the angle between the two original vectors and how it points in the direction perpendicular to both, with a brief mention of torque in physics and calculus.

20:03

📏 Properties of the Cross Product: Length and Scalar Triple Product

The script explores the properties of the cross product, focusing on its length, which is related to the sine of the angle between the two original vectors. It draws a parallel between the cross product and the dot product, emphasizing the difference in the trigonometric function used (sine for cross, cosine for dot). The concept of the scalar triple product is introduced as a combination of the cross and dot products, and its implications for determining whether three vectors are coplanar are discussed. The scalar triple product is also related to the volume of a parallelepiped formed by the vectors.

25:05

📐 Geometric Representation of the Scalar Triple Product

The final paragraph provides a geometric interpretation of the scalar triple product, explaining how it can be visualized as the volume of a parallelepiped. The instructor describes how the absolute value of the scalar triple product represents this volume, ensuring it is always a positive value. The explanation connects the scalar triple product to the lengths of the vectors involved and the angle between them, offering a method for calculating it using determinants or geometric relationships.

30:05

🔚 Conclusion on Scalar Triple Product and Vector Relationships

The script concludes with a brief mention of the scalar triple product's geometric representation, indicating how it can be used to determine the height of a parallelepiped when the base area and the horizontal component of the cross product are known. This final note reinforces the practical applications of the scalar triple product in understanding the spatial relationships between vectors.

Mindmap

Keywords

💡Cross Product

The cross product is a mathematical operation that takes two vectors in three-dimensional space and returns a third vector that is perpendicular to the first two, indicating a direction out of the plane formed by the original vectors. It is central to the video's theme as it is the main topic being discussed. For instance, the script explains how to calculate the cross product using determinants and the right-hand rule, emphasizing its geometric interpretation and applications in physics, such as calculating torque.

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two vectors and returns a scalar value. It is used to determine the angle between two vectors and is related to the magnitude of the vectors. In the script, the dot product is contrasted with the cross product, highlighting the difference in outcome—scalar versus vector—and the script mentions that the dot product is used to establish the relationship between the angle of two vectors and their magnitudes.

💡Determinant

A determinant is a scalar value that is the result of a specific matrix calculation. In the context of the video, the determinant is used to calculate the cross product of two vectors by arranging the vector components into a matrix and applying the determinant formula. The script introduces the determinant as a preliminary concept necessary for understanding the cross product, especially in the case of 2x2 and 3x3 matrices.

💡Right-Hand Rule

The right-hand rule is a common mnemonic for understanding the direction of the cross product in three dimensions. By aligning the fingers of the right hand to represent two vectors, the thumb points in the direction of the cross product. The script uses the right-hand rule to illustrate the orientation of the cross product vector in relation to the original vectors and to help visualize the concept of orthogonality.

💡Orthogonal

Orthogonality refers to the property of two lines or vectors being perpendicular to each other, forming a right angle. In the script, it is mentioned that the cross product of two vectors results in a vector that is orthogonal to both of the original vectors, emphasizing the geometric interpretation of the cross product.

💡Matrix

A matrix is a rectangular array of numbers arranged in rows and columns. In the video, matrices are used to organize the components of vectors for calculations, particularly in determining the cross and dot products. The script explains how to set up a matrix for calculating the determinant, which is essential for finding the cross product of two vectors.

💡Scalar Triple Product

The scalar triple product is a mathematical expression that involves taking the dot product of a vector with the cross product of two other vectors. It is used to determine if three vectors are coplanar or to calculate the volume of a parallelepiped formed by the vectors. The script discusses the scalar triple product in the context of the cross product, explaining its geometric interpretation and how it can be calculated using determinants.

💡Parallelepiped

A parallelepiped is a three-dimensional figure formed by six parallelograms. In the script, the concept of a parallelepiped is used to explain the geometric interpretation of the scalar triple product, which can be used to calculate the volume of such a shape formed by three vectors in three-dimensional space.

💡Torque

Torque is a measure of the force's tendency to cause rotational motion about an axis. Although not the main focus of the video, the script briefly mentions torque in the context of the cross product, indicating its relevance in physics, particularly when calculating the rotational effect of a force applied at a distance from the pivot point.

💡Coplanar

Coplanar vectors are vectors that lie in the same plane. The script discusses the concept of coplanarity in the context of the scalar triple product, explaining that if the scalar triple product of three vectors is zero, it indicates that the vectors are coplanar, meaning they all lie in the same two-dimensional plane.

Highlights

Introduction to the cross product, a method to multiply two vectors resulting in a new vector.

Difference between the dot product and cross product: the former results in a scalar, the latter in a vector.

Importance of the determinant in calculating the cross product, with an introduction to its concept.

Explanation of how to set up a matrix with two vectors in R2 for determinant calculation.

Clarification on the naming convention for matrices and the process of creating a matrix from vectors.

Understanding the concept of main and secondary diagonals in a matrix for determinant calculation.

The determinant as a numerical value resulting from matrix operations, not a vector.

Expansion to 3x3 matrices and the method of breaking down into 2x2 determinants.

Memory aid for 3x3 determinant calculation using alternating sums and sub-determinants.

The cross product's definition as a vector orthogonal to the original two vectors.

The right-hand rule for visualizing the direction of the cross product.

Torque and its relation to the cross product in physics and calculus.

Cross product's properties when the vectors are parallel, resulting in a zero vector.

The length of the cross product as the product of the magnitudes of the vectors and the sine of the angle between them.

The scalar triple product, its calculation, and its relation to the volume of a parallelepiped.

Geometric interpretation of the scalar triple product involving the cross product and dot product.

Condition for vectors being coplanar based on the scalar triple product being zero.

Practical application of the scalar triple product in determining the volume of a parallelepiped.

Transcripts

Browse More Related Video

Geometrically Defining the Cross Product | Multivariable Calculus

Cross Product and Dot Product: Visual explanation

Angular momentum and cross product

Calculus 3: The Cross Product (Video #4) | Math with Professor V

Cross Product (Introduction)

Cross Product of Two Vectors Explained!

Related Tags

Vector Math Cross Product Dot Product Determinant Right Hand Rule Torque Scalar Triple Product 3D Geometry Educational Script Mathematics Tutorial Linear Algebra