Calculus 3: The Cross Product (Video #4) | Math with Professor V
TLDRThis calculus lecture introduces the cross product of two vectors in three-dimensional space, distinguishing it from the dot product. The formula for the cross product is presented, and the use of determinants as a memory aid is explained. The video demonstrates how to calculate the cross product, discusses its properties, and highlights its applications, such as finding vectors orthogonal to a given set and determining the volume of parallelepipeds. The script also covers the geometric interpretation of the cross product, including its relation to the area of parallelograms and the concept of coplanarity in four points.
Takeaways
- 📚 The cross product, also known as the vector product, is a mathematical operation that takes two vectors in three-dimensional space and returns a vector, as opposed to the dot product which results in a scalar.
- ⚠️ The cross product is only defined in three-dimensional vector space, and it is different from the dot product, which can be used in n-dimensional space.
- 🔍 The formula for the cross product of two vectors \( \mathbf{a} \) and \( \mathbf{b} \) with components \( (a_1, a_2, a_3) \) and \( (b_1, b_2, b_3) \) respectively is given by \( \mathbf{a} \times \mathbf{b} = (a_2b_3 - a_3b_2, a_3b_1 - a_1b_3, a_1b_2 - a_2b_1) \).
- 📈 To aid in memorization, the cross product can be calculated using determinants, specifically a 3x3 matrix with unit vectors \( \mathbf{i}, \mathbf{j}, \mathbf{k} \) in the first row and the components of the two vectors in the next two rows.
- 🔄 The cross product does not satisfy the commutative property; instead, \( \mathbf{a} \times \mathbf{b} = -\(\mathbf{b} \times \mathbf{a}\) \), meaning the cross product of two vectors in reverse order is the negative of the original cross product.
- 📉 The cross product of a vector with itself is the zero vector, which can be proven by setting up a 3x3 determinant with the same vector in the last two rows and calculating the result.
- 📐 The cross product vector is orthogonal to both of the original vectors, a property that can be used to find vectors that are perpendicular to a given set of vectors.
- 📏 The magnitude of the cross product of two vectors is equal to the product of the magnitudes of the two vectors and the sine of the angle between them, which can be used to find the area of a parallelogram formed by the vectors.
- 🤔 The cross product can be used to determine if two vectors are parallel by checking if the magnitude of their cross product is zero, although this is not the most practical method.
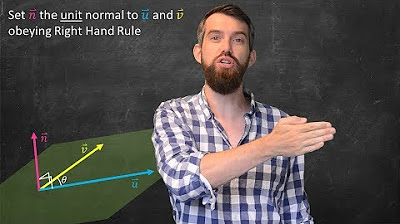
- 📐 The direction of the cross product vector is determined by the right-hand rule, which states that if the fingers of the right hand curl from vector \( \mathbf{a} \) to vector \( \mathbf{b} \), the thumb points in the direction of \( \mathbf{a} \times \mathbf{b} \).
- 📏 The magnitude of the cross product can also be interpreted as the area of the parallelogram determined by the two vectors, which is a useful geometric application of the cross product.
Q & A
What is the main difference between the dot product and the cross product of two vectors?
-The dot product of two vectors results in a scalar quantity, whereas the cross product results in a vector. The cross product is specifically defined in three-dimensional vector space, unlike the dot product which can work in n-dimensional space.
How is the cross product of two vectors defined mathematically?
-If you have two vectors A with components (a1, a2, a3) and B with components (b1, b2, b3), the cross product A x B is defined with the components: (a2 * b3 - a3 * b2), (a3 * b1 - a1 * b3), and (a1 * b2 - a2 * b1).
Why is it difficult to memorize the formula for the cross product?
-The formula for the cross product can be challenging to memorize due to its complexity. To help with this, determinants and matrices are often used as a memory device, even though the cross product itself does not involve a determinant.
What is the significance of the right-hand rule in the context of the cross product?
-The right-hand rule is used to determine the direction of the cross product vector. If the fingers of the right hand curl from vector A towards vector B, the thumb points in the direction of the cross product A x B.
How does the magnitude of the cross product relate to the vectors being crossed and the angle between them?
-The magnitude of the cross product |A x B| is equal to the product of the magnitudes of vectors A and B and the sine of the angle θ between them, expressed as |A| * |B| * sin(θ).
What property of the cross product indicates its orthogonality to the original vectors?
-The cross product A x B is orthogonal to both vectors A and B, meaning it is mutually perpendicular to the two vectors that were crossed.
Can the cross product be used to determine if two vectors are parallel?
-While theoretically the cross product can indicate if two vectors are parallel by having a magnitude of zero, in practice, it is more common and simpler to verify if vectors are parallel by showing one is a scalar multiple of the other.
How is the cross product used to find the area of a parallelogram formed by two vectors?
-The magnitude of the cross product of two vectors A and B gives the area of the parallelogram they form, as it is equivalent to the base times the height of the parallelogram, where the height is the perpendicular distance from one vector to the other.
What is the geometric interpretation of the triple scalar product, and how is it related to the volume of a parallelepiped?
-The triple scalar product, such as A · (B x C), gives a scalar value that is equal to the volume of the parallelepiped formed by vectors A, B, and C. The absolute value of this product ensures a non-negative volume.
How can the triple scalar product be used to determine if four points are coplanar?
-If the triple scalar product of vectors formed by four points is zero, it indicates that the points are coplanar, as they would form a degenerate parallelepiped with zero volume.
Outlines
📚 Introduction to the Cross Product in Calculus
The video lecture introduces the concept of the cross product, also known as the vector product, which is a method of multiplying two vectors in three-dimensional space to yield another vector, unlike the dot product which results in a scalar. The cross product is specific to three-dimensional vectors, but can be adapted for two-dimensional vectors by setting the third component to zero. The formula for the cross product of two vectors A and B with components (a1, a2, a3) and (b1, b2, b3) is given, and the video suggests using determinants as a memory aid for the formula. The process of calculating the cross product using a 3x3 determinant involving unit vectors i, j, and k is explained, with the determinant expanded along the top row to find the components of the resulting vector.
🔍 Calculating the Cross Product with Examples
The script provides a step-by-step guide on calculating the cross product, including a practical example using vectors (2, 0, -3) and (1, 6, 0). It demonstrates the process of setting up a 3x3 matrix with unit vectors and the given vectors, calculating the determinant, and finding the resulting cross product vector. The video also explores the non-commutative property of the cross product, showing that reversing the order of the vectors results in a vector in the opposite direction. A trick for simplifying the calculation by rearranging the subtraction order is shared, along with a method for quickly computing the cross product without writing out the full determinant.
📉 Proving Properties of the Cross Product
The script delves into proving that the cross product of a vector with itself results in the zero vector, which is a fundamental property of the cross product. It also discusses the theorem that the cross product of two vectors is orthogonal to both of the original vectors, providing a geometric interpretation of this property. An example problem is presented, where the cross product is used to find two unit vectors that are orthogonal to two given vectors, illustrating the application of the cross product in vector analysis.
🧭 Direction and Magnitude of the Cross Product
The direction of the cross product is determined using the right-hand rule, which is explained in the script. The magnitude of the cross product is derived from the sine of the angle between the two vectors, leading to the conclusion that the magnitude of the cross product equals the product of the magnitudes of the two vectors and the sine of the angle between them. The script also discusses how the cross product can be used to determine if two vectors are parallel, although it notes that this is not a common practice due to the simplicity of checking for scalar multiples.
📏 Cross Product and Geometric Applications
The script explores the geometric interpretation of the magnitude of the cross product, relating it to the area of a parallelogram formed by two vectors. It also discusses the properties of the cross product, such as the lack of commutativity and associativity, and the distributive property over vector addition. The concept of the triple scalar product is introduced, which is used to determine the volume of a parallelepiped formed by three vectors. The script concludes with an example of using the triple scalar product to verify whether four points are coplanar.
📐 Practical Applications of the Cross Product
The final paragraph of the script focuses on practical applications of the cross product, such as finding a vector orthogonal to a plane defined by three points and calculating the area of a triangle formed by two vectors. The process of using the cross product to determine the area of the parallelogram and then halving it to find the area of the triangle is explained. The script emphasizes the importance of understanding and being able to compute the cross product for further studies in calculus.
Mindmap
Keywords
💡Cross Product
💡Dot Product
💡Determinant
💡Orthogonal
💡Unit Vector
💡Magnitude
💡Right-Hand Rule
💡Commutative Property
💡Scalar
💡Triple Scalar Product
💡Coplanar
Highlights
Introduction to the cross-product, also known as the vector product, which results in a vector rather than a scalar.
Cross-product is defined in three-dimensional vector space and can be applied in two-dimensional space with the third component set to zero.
The definition of the cross-product formula using components of two vectors a and b.
Use of matrices and determinants as a memory device for the cross-product formula.
The method to calculate the cross-product using a 3x3 determinant with unit vectors i, j, k.
Illustration of the cross-product calculation between two vectors and the demonstration of non-commutative property.
Proof that the cross-product of a vector with itself yields the zero vector.
Theorem stating that the cross-product vector is orthogonal to both original vectors.
Application of the cross-product to find unit vectors orthogonal to given vectors.
Explanation of the right-hand rule for determining the direction of the cross-product vector.
Derivation of the magnitude of the cross-product in terms of the magnitudes of the original vectors and the sine of the angle between them.
Application of the cross-product to determine if two vectors are parallel.
Geometric interpretation of the magnitude of the cross-product as the area of the parallelogram formed by two vectors.
Properties of the cross-product, including non-commutativity and distribution over vector addition.
Introduction of the triple scalar product and its geometric interpretation as the volume of a parallelepiped.
Use of the triple scalar product to verify if four points are coplanar.
Application of the cross-product to find a vector orthogonal to a plane defined by three points.
Calculation of the area of a triangle using the cross-product of two vectors representing two sides of the triangle.
Conclusion summarizing the importance of understanding and being able to compute the cross-product for further studies in calculus.
Transcripts
Browse More Related Video

Calculus 3: Lecture 11.4 The Cross Product of Two Vectors in Space

Lec 2: Determinants; cross product | MIT 18.02 Multivariable Calculus, Fall 2007
Geometrically Defining the Cross Product | Multivariable Calculus

Ch. 9.5 The Cross Product

why there is no four dimensional cross product.

Finding Areas Using the Cross Product (Calculus 3)
5.0 / 5 (0 votes)
Thanks for rating: