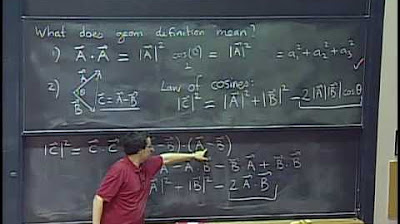Calculus 3: The Dot Product (Video #3) | Math with Professor V

Math with Professor V

1 Jun 202036:45

EducationalLearning

32 Likes 10 Comments

TLDRThis calculus lecture introduces the dot product, also known as the scalar product or inner product, a fundamental operation for vector multiplication resulting in a scalar rather than another vector. The script explains the dot product's definition, properties, and proofs, and explores its applications, such as finding the angle between vectors, determining orthogonality, and calculating work done by a force. It also covers concepts like direction angles, direction cosines, and projections, providing examples to solidify understanding.

Takeaways

📚 The lecture introduces the concept of vector multiplication, focusing on the dot product and the cross product, with the dot product being the main topic of the video.
🔍 The dot product, also known as the scalar product or inner product, results in a scalar quantity rather than a vector when two vectors are multiplied.
📝 The formula for the dot product of two vectors is given by multiplying corresponding components and summing the results, requiring the vectors to be of the same dimension.
📈 An example is provided to illustrate the calculation of the dot product for two vectors, emphasizing the use of a dot symbol for this operation.
🔄 Properties of the dot product are discussed, including commutativity, distributivity, and the relationship between the dot product and the magnitude of a vector.
📐 The proof of the distributive property of the dot product over vector addition is demonstrated, highlighting the importance of a step-by-step approach in proofs.
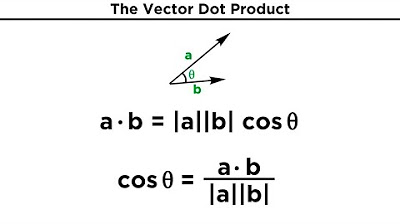
📏 The concept of the angle between two vectors is explored, using the dot product and the law of cosines to establish a relationship between the angle and the vectors' magnitudes.
🛑 The orthogonality of vectors is defined, where two vectors are orthogonal if their dot product equals zero, indicating a perpendicular relationship.
🧭 The direction angles and direction cosines of a vector are introduced, explaining how they relate to the angles a vector makes with the coordinate axes and its components.
📉 The sum of the squares of the direction cosines of a vector is shown to equal 1, a property derived from the Pythagorean theorem.
🔄 The concept of vector projection is discussed, explaining how to find the scalar and vector projections of one vector onto another, including the use of these concepts in calculating work done by a force.

Q & A

What are the two main types of vector multiplication discussed in the script?
-The two main types of vector multiplication discussed are the dot product and the cross product. The dot product results in a scalar, while the cross product results in another vector.
What is the dot product also known as?
-The dot product is also referred to as the scalar product or the inner product.
How is the dot product of two vectors defined?
-The dot product of two vectors is defined as the sum of the products of their corresponding components, resulting in a scalar quantity.
What is a necessary condition for two vectors to be multiplied using the dot product?
-A necessary condition for two vectors to be multiplied using the dot product is that they must have the same dimension.
What does the dot product of a vector with itself represent?
-The dot product of a vector with itself represents the magnitude of the vector squared.
What is the commutative property of the dot product?
-The commutative property of the dot product states that the dot product of two vectors A and B is equal to the dot product of B and A (A · B = B · A).
How can you determine if two vectors are orthogonal?
-Two vectors are orthogonal if their dot product is equal to zero.
What is the relationship between the dot product and the angle between two vectors?
-The dot product of two vectors is equal to the product of their magnitudes and the cosine of the angle between them (A · B = |A| * |B| * cos(θ)).
What is the definition of scalar projection?
-Scalar projection is the component of one vector along another vector, calculated as the dot product of the two vectors divided by the magnitude of the vector onto which you are projecting.
How can you find the vector projection of one vector onto another?
-To find the vector projection of one vector onto another, you first calculate the scalar projection, then multiply this scalar by the unit vector in the direction of the vector you are projecting onto.
What is the formula for calculating work done by a force in the direction of displacement?
-The work done by a force in the direction of displacement is calculated as the dot product of the force vector and the displacement vector, which can also be expressed as the product of the magnitudes of the force and displacement vectors and the cosine of the angle between them.

Outlines

00:00

📚 Introduction to Dot Product

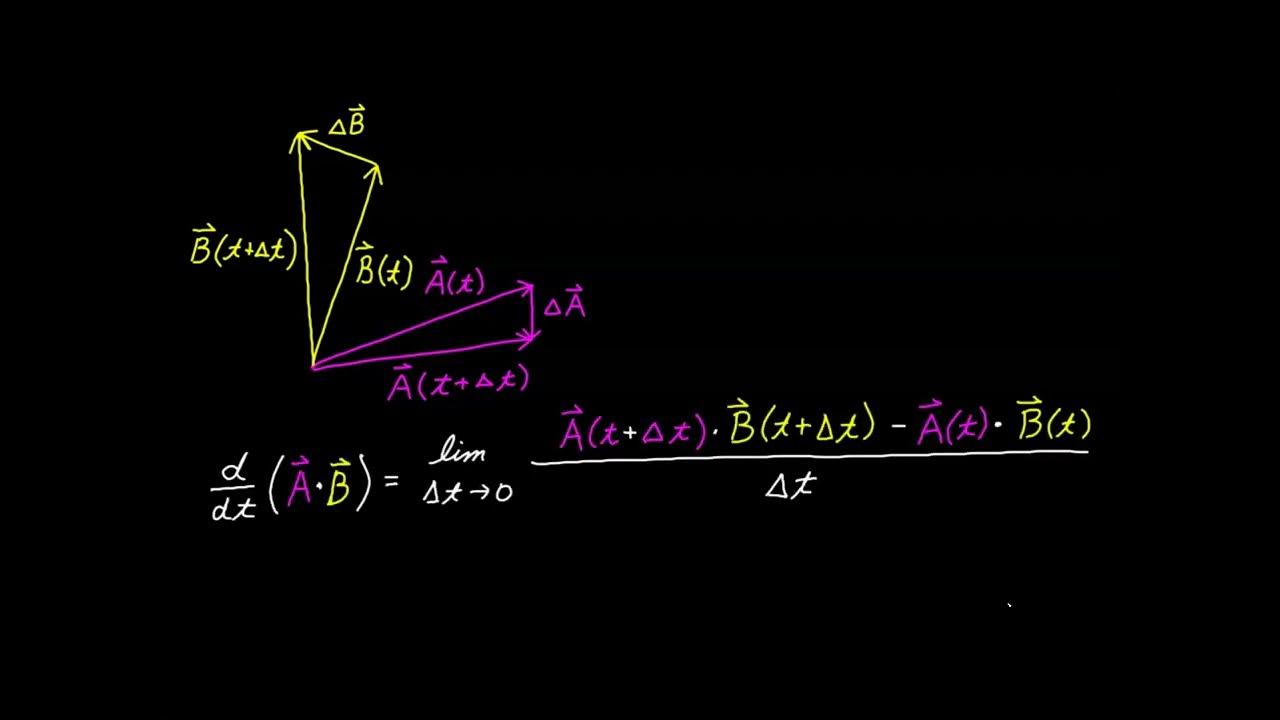
The video lecture begins with an introduction to the dot product, also known as the scalar product or inner product. The dot product is a method of multiplying two vectors that results in a scalar, not another vector. The definition of the dot product is given, explaining that it involves multiplying corresponding components of two vectors and summing these products. The lecture emphasizes the importance of matching dimensions between vectors for the operation to be valid. An example calculation is provided to illustrate the process. The section concludes with a brief overview of the properties of the dot product, such as commutativity and distributivity, and introduces the concept of proving these properties through mathematical proofs.

05:04

🔍 Properties and Proof of Dot Product

This paragraph delves deeper into the properties of the dot product, including its commutative and distributive nature, and the fact that the dot product of any vector with itself equals the square of its magnitude. A step-by-step proof is provided to demonstrate the distributive property of the dot product over scalar multiplication. The proof involves defining vectors and their components, distributing the scalar across the vector, applying the dot product definition, and using the distributive property in reverse to arrive at the conclusion. The paragraph encourages students to practice proving other properties of the dot product.

10:04

📐 Dot Product and Angle Between Vectors

The lecture continues by exploring the relationship between the dot product and the angle between two vectors. It introduces the concept of using the law of cosines to relate the dot product to the magnitudes of the vectors and the cosine of the angle between them. The paragraph explains how the dot product can be used to find the angle between two vectors by rearranging the formula derived from the law of cosines. An example calculation is provided to demonstrate how to find the angle between two given vectors, emphasizing the use of the corollary derived from the properties of the dot product.

15:09

🦴 Orthogonal Vectors and Direction Angles

The concept of orthogonal vectors is introduced, where two vectors are orthogonal if their dot product is zero. The paragraph also discusses direction angles and direction cosines of a vector in three-dimensional space. It explains how to calculate the direction angles using the dot product with the unit vectors along the axes. The relationship between the squares of the direction cosines summing up to one is highlighted, and the concept of a unit vector in the direction of a given vector is explained. An example is provided to calculate the direction angles of a specific vector.

20:10

📐 Scalar and Vector Projections

This section introduces the concepts of scalar and vector projections. The scalar projection is described as the component of one vector along another, calculated using the dot product and magnitudes of the vectors. The vector projection is explained as the process of finding a vector that lies in the direction of another vector and has the same length as the scalar projection. The paragraph provides a clear explanation of how to calculate both the scalar and vector projections, including the use of unit vectors to maintain direction while adjusting magnitude. An example is given to illustrate the process of finding the scalar and vector projections of one vector onto another.

25:11

🔨 Orthogonal Projection and Work Calculation

The lecture concludes with the concept of orthogonal projection, which is the component of a vector that is perpendicular to another vector. The definition and calculation method for orthogonal projection are provided, using vector subtraction to find the component of one vector that is perpendicular to another. The paragraph also revisits the concept of work from physics, explaining how work can be calculated using the scalar projection of the force vector along the direction of displacement. An example of calculating work done in pulling a wagon is provided, demonstrating the application of the dot product in physics.

30:14

🚀 Conclusion and Upcoming Cross Product

In the final paragraph, the lecture wraps up the discussion on the dot product and teases the next topic, the cross product. The importance of understanding and memorizing the definitions and properties of the dot product is emphasized for their application in future lessons. The paragraph serves as a conclusion to the current topic and a bridge to the next part of the course, maintaining the viewer's interest and setting the stage for continued learning.

Mindmap

Keywords

💡Dot Product

The dot product, also known as the scalar product or inner product, is a mathematical operation that takes two vectors and returns a scalar. It is calculated by multiplying corresponding components of the vectors and summing the results. In the context of the video, the dot product is introduced as the first type of vector multiplication, emphasizing that the result is not a vector but a scalar quantity. The script provides the formula for the dot product and demonstrates its calculation with an example using vectors.

💡Cross Product

Although not the main focus of the video, the cross product is mentioned as the second type of vector multiplication. Unlike the dot product, the cross product results in a vector. The script indicates that the cross product will be the subject of a subsequent lesson, suggesting its importance in the broader study of vector operations.

💡Scalar

A scalar is a single numerical value, as opposed to a vector, which has both magnitude and direction. In the video, the term 'scalar' is used to describe the result of the dot product, highlighting the fundamental difference between vector and scalar quantities. The script explains that multiplying two vectors using the dot product does not yield another vector but instead a single numerical value.

💡Vector Components

Vector components refer to the individual elements of a vector that define its position in space. In the script, the components of vectors are used to calculate the dot product by multiplying corresponding components together. The video emphasizes the necessity for both vectors to have the same dimension for the dot product to be computed.

💡Magnitude

The magnitude of a vector is its length or size, calculated from the square root of the sum of the squares of its components. The script uses the concept of magnitude to explain properties of the dot product, such as how a vector dotted with itself equals the magnitude squared, and to calculate work done by a force.

💡Commutative Property

The commutative property of the dot product states that the order of the vectors does not affect the result. The script mentions this property as one of the fundamental properties of the dot product, illustrating that A dot B is equal to B dot A.

💡Orthogonal Vectors

Orthogonal vectors are vectors that are perpendicular to each other, and their dot product is zero. The script introduces the concept of orthogonality and explains how the dot product can be used to determine if two vectors are orthogonal, which is a key concept in understanding vector relationships.

💡Direction Angles

Direction angles are the angles a vector makes with the positive axes of a coordinate system. The script discusses how to find the direction angles of a vector in three-dimensional space using the dot product and the components of the unit vectors along each axis.

💡Direction Cosines

Direction cosines are the cosines of the direction angles and represent the components of a unit vector in the direction of another vector. The video explains how to calculate the direction cosines using the dot product and how they relate to the components of a unit vector.

💡Scalar Projection

Scalar projection is the length of the component of one vector in the direction of another vector. The script defines scalar projection and explains how it is calculated using the dot product. It is used to determine the magnitude of a vector's projection onto another vector.

💡Vector Projection

Vector projection is the vector equivalent of scalar projection, representing the component of one vector in the direction of another as a vector. The script describes how to calculate vector projection by using the scalar projection and a unit vector in the direction of the second vector.

💡Orthogonal Projection

Orthogonal projection refers to the component of a vector that is perpendicular to another vector. The script explains how to find the orthogonal projection of a vector with respect to another vector by using vector subtraction and the concept of vector projection.

💡Work

In the context of physics, work is the product of the force applied to an object and the displacement of the object in the direction of the force. The script relates the concept of work to the dot product by explaining that work can be calculated as the dot product of the force and displacement vectors when the force is constant and applied at an angle to the direction of motion.

Highlights

Introduction to the dot product, also known as the scalar product or inner product, which results in a scalar rather than a vector.

Explanation of the dot product formula involving the multiplication of corresponding components of two vectors.

Requirement for vectors to have the same dimension for the dot product to be computed.

Example calculation of the dot product for vectors (7, -1, 3, 0) and (3, 0, 4).

Properties of the dot product, including commutativity and distributivity.

Proof of the property that a dot product with a scalar multiple of a vector equals the scalar times the dot product of the vectors.

Application of the dot product in finding the angle between two vectors using the law of cosines.

Corollary for calculating the angle between two vectors using the dot product and their magnitudes.

Orthogonality definition where two vectors are orthogonal if their dot product is zero.

Method to determine if two vectors are orthogonal by calculating their dot product.

Introduction to direction angles and direction cosines of a vector in three-dimensional space.

Calculation of direction angles using the dot product and magnitude of a vector.

Pythagorean identity that the sum of the squares of the direction cosines equals one.

Concept of scalar projection, which is the component of one vector along another vector.

Formula for scalar projection and its geometric interpretation.

Vector projection, which involves scaling the scalar projection to a vector in the direction of the second vector.

Orthogonal projection, which is the vector perpendicular to the projection of one vector onto another.

Example calculations of scalar, vector, and orthogonal projections for given vectors.

Application of the dot product in calculating work done by a force on an object when the force is applied at an angle to the displacement.

Example of calculating work done pulling a wagon with a force at a 30-degree angle to the horizontal.

Transcripts

Browse More Related Video

Ch. 9.2 The Dot Product

Lec 1: Dot product | MIT 18.02 Multivariable Calculus, Fall 2007

Video 14 - Dot Product

The Vector Dot Product

Finding the Vector Dot Product

Dot Products (In 3-dimensional Space)

Related Tags

Dot Product Vector Multiplication Calculus Tutorial Scalar Product Inner Product Vector Operations Cross Product Introduction Vector Properties Angle Calculation Work Calculation