Euler Squares - Numberphile
TLDRThe video script presents a complex puzzle involving arranging cards in a 4x4 grid to satisfy multiple constraints, akin to Sudoku, but with an added twist of suits. It delves into the concept of Latin squares and their extension to Greco-Latin squares, highlighting their applications in statistics and experimental design. The script also explores Euler's conjecture on the impossibility of certain sized Latin squares and the eventual debunking of this belief, emphasizing that even renowned mathematicians can be mistaken.
Takeaways
- 🃏 The puzzle involves arranging cards in a 4x4 grid with each row, column, and diagonal containing an Ace, King, Queen, and Jack, as well as a club, heart, spade, and diamond.
- 🧩 The puzzle is likened to Sudoku, suggesting a logical and systematic approach to finding a solution.
- 🔄 The importance of swapping cards to test different arrangements is highlighted as a strategy for solving the puzzle.
- 📝 The speaker recommends using pen and paper to solve the puzzle, drawing parallels to solving Sudoku.
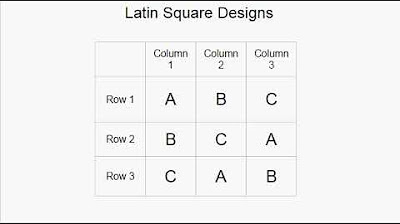
- 🔑 The concept of a Latin square is introduced, where each row and column contains a unique set of elements without repetition.
- 🎲 The script explains a double Latin square, which is a superimposition of two Latin squares with different sets of elements.
- 📊 The practical application of Latin squares in statistics and experimental design is discussed, particularly in eliminating biases in tournament or experiment setups.
- 🏓 An example of a ping-pong tournament is given to illustrate how Latin squares can ensure fairness and allow for accurate comparisons between players.
- 🤔 The script explores the history and mathematical challenges of constructing Latin squares of different sizes, noting that not all sizes are possible.
- 🔢 Euler's conjecture about the impossibility of certain Latin square sizes, such as 6x6, is mentioned, along with the eventual disproval of some of his assertions.
- 🛠 The use of computers in the construction and proof of 'impossible' Latin squares, such as the 10x10 and 22x22, is highlighted, showcasing the evolution of mathematical problem-solving.
- 🏳️ The final takeaway emphasizes that even renowned mathematicians like Euler can be mistaken, and it underscores the importance of continuous exploration and verification in mathematics.
Q & A
What is the puzzle presented in the video about?
-The puzzle is about arranging Aces, Kings, Queens, and Jacks from a deck of cards in a 4x4 grid such that every row, column, and diagonal contains one of each card and one of each suit (clubs, hearts, spades, and diamonds).
How does the presenter compare the puzzle to Sudoku?
-The presenter compares the puzzle to Sudoku because it requires logical placement of elements (cards and suits) in a grid with the same constraints of no repetition in rows, columns, and diagonals.
What is a Latin square according to the video?
-A Latin square is an arrangement of n different symbols in a square grid, where each symbol appears exactly once in each row and exactly once in each column.
What is a double Latin square or a Greco-Latin square?
-A double Latin square, also known as a Greco-Latin square, is a pair of Latin squares of the same order where the two squares are superimposed upon each other in such a way that each pair of corresponding entries from the two squares is different.
How are Latin squares used in statistics and experimental design?
-Latin squares are used in statistics and experimental design to ensure that all conditions are equally represented and to eliminate bias, allowing for fair comparisons and accurate analysis of experimental results.
What is the 36 officers problem mentioned in the video?
-The 36 officers problem is a specific case of the general problem of constructing a 6x6 Latin square, which Euler conjectured to be impossible. It involves arranging six regiments, each with six officers of different ranks, into a square grid such that no two officers of the same rank are in the same row or column.
Why did Euler believe that 6x6, 10x10, 14x14, and similar grids could not have Latin squares?
-Euler believed these sizes to be impossible because he could not find a solution despite his attempts, and he thought that without checking every possibility, there was no way to prove it, which he considered impractical.
What did Gaston Tarry do to prove Euler's conjecture about the impossibility of a 6x6 Latin square?
-Gaston Tarry checked every possibility, which amounted to 9408 different arrangements, to prove that a 6x6 Latin square is indeed impossible.
How did Raj Bose challenge Euler's conjecture regarding the impossibility of certain Latin square sizes?
-Raj Bose constructed a 22x22 Latin square, which was thought to be impossible according to Euler's conjecture, thus showing that Euler could be wrong and that there were methods to construct these supposedly impossible grids.
What is the current understanding of which sizes of Latin squares are impossible?
-Currently, it is known that only 2x2 and 6x6 Latin squares are impossible. All other sizes, including those that Euler initially conjectured to be impossible, can be constructed.
Why should one not arrange a ping-pong tournament with six team members according to the video?
-One should not arrange a ping-pong tournament with six team members because it would be impossible to create a fair schedule where each player plays at different times and against all other players, due to the impossibility of a 6x6 Latin square.
Outlines
🃏 Card Puzzle Introduction and Strategy
The video introduces a complex card puzzle reminiscent of Sudoku, which involves arranging Aces, Kings, Queens, and Jacks in a 4x4 grid with each row, column, and diagonal containing one of each card rank and one of each suit. The presenter discusses the challenge of ensuring that no two identical ranks or suits appear in the same column or diagonal. They suggest treating it like a Sudoku and using pen and paper to find a solution, eventually demonstrating a methodical approach to solving the puzzle by placing cards in a way that satisfies all the conditions, resulting in a double Latin square.
🎱 Real-Life Applications of Latin Squares in Statistics
This paragraph delves into the practical applications of Latin squares in statistics, particularly in the design of experiments. It uses the example of a ping-pong tournament to illustrate how Latin squares can ensure fairness by arranging matches in such a way that every player competes against every other player and plays in every time slot, allowing for unbiased comparisons. The concept is extended to the idea of a double Latin square, where two sets of Latin squares are superimposed, with each combination of elements appearing exactly once, a concept known as a Greco-Latin square.
🔢 Historical Exploration of Greco-Latin Squares and Euler's Conjecture
The final paragraph discusses the historical aspect of Greco-Latin squares, focusing on Euler's conjecture regarding their impossibility for certain sizes, specifically 6x6 and multiples of 6. It recounts Euler's unsuccessful attempts to create such squares and his eventual conclusion that they were impossible. The paragraph also mentions the later disproof of this conjecture for 10x10 and higher even-numbered squares by mathematicians using computers, highlighting the discovery of 'Euler Spoilers' and the correction of Euler's long-standing belief, emphasizing that even renowned mathematicians can be mistaken.
Mindmap
Keywords
💡Puzzle
💡Latin Square
💡Greco-Latin Square
💡Sudoku
💡Diagonals
💡Experiment Design
💡Bias
💡Ping-Pong Tournament
💡Euler
💡36 Officers Problem
💡Numberphile
Highlights
Introduction of a 4x4 card puzzle with a unique arrangement requirement involving suits and face cards.
Comparison of the puzzle to Sudoku, emphasizing the need for logical arrangement.
Explanation of the puzzle's constraints: no duplicates in rows, columns, or diagonals for both card ranks and suits.
The presenter's approach to solving the puzzle by swapping cards to meet the puzzle's requirements.
Mistakes made and the process of correcting them to find a valid solution.
The concept of a Latin square and its relation to the puzzle, explained with an example.
Introduction of a double Latin square, where two Latin squares are superimposed.
Real-life applications of Latin squares in statistics and experimental design.
The use of Latin squares in organizing tournaments to ensure fairness and unbiased comparison.
Euler's investigation into the possibility of Greco-Latin squares for different sizes and his conjectures.
The historical resolution of Euler's conjecture by Gaston Tarry for the 6x6 case.
The discovery of 'Euler Spoilers' that contradicted Euler's conjecture for certain even-numbered grids.
The role of computers in constructing and proving the existence of previously thought impossible Greco-Latin squares.
The final conclusion that only 2x2 and 6x6 Greco-Latin squares are impossible.
A humorous note on Euler's error and the advice against arranging a ping-pong tournament with six team members.
An extension of the puzzle to include a third Latin square with different shapes.
Acknowledgment of Patreon supporters and the impact of their contributions on the content's quality.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: