Impossible Squares - Numberphile
TLDRIn this engaging video script, the concept of drawing squares on a gridded paper is explored, leading to a deeper investigation into the mathematical problem of which numbers can be expressed as the sum of two squares. The discussion starts with simple square numbers and evolves into a proof of Pythagoras' theorem using the dot grid. It then delves into number theory, revealing a connection between prime factors and the impossibility of representing certain numbers as sums of squares, with a simple test involving prime factors of the form (4k+3) raised to an odd power.
Takeaways
- 📏 The script discusses the problem of drawing squares on a grid of dots, using straight lines between dots to form square shapes.
- 🔢 It highlights that the areas of the squares drawn are perfect squares, such as 1, 4, 9, and 16, because the sides of the squares are integer lengths.
- 🤔 The conversation explores the possibility of drawing squares with areas that are not perfect squares, such as 20, by using slanted lines to form the squares.
- 📐 The script introduces the concept of (a, b) notation to represent slanted squares, where 'a' and 'b' are the distances moved in two perpendicular directions on the grid.
- 🧩 It is shown that the area of a slanted square can be calculated by the formula a^2 + b^2, which is a proof of Pythagoras' theorem in a different context.
- 📉 The script identifies numbers that cannot be drawn as squares on the grid, such as 3, 6, 7, and 11, by demonstrating that they cannot be expressed as the sum of two squares.
- 📈 The exploration escalates into a number theory question, specifically asking which integers can be expressed as the sum of two squares.
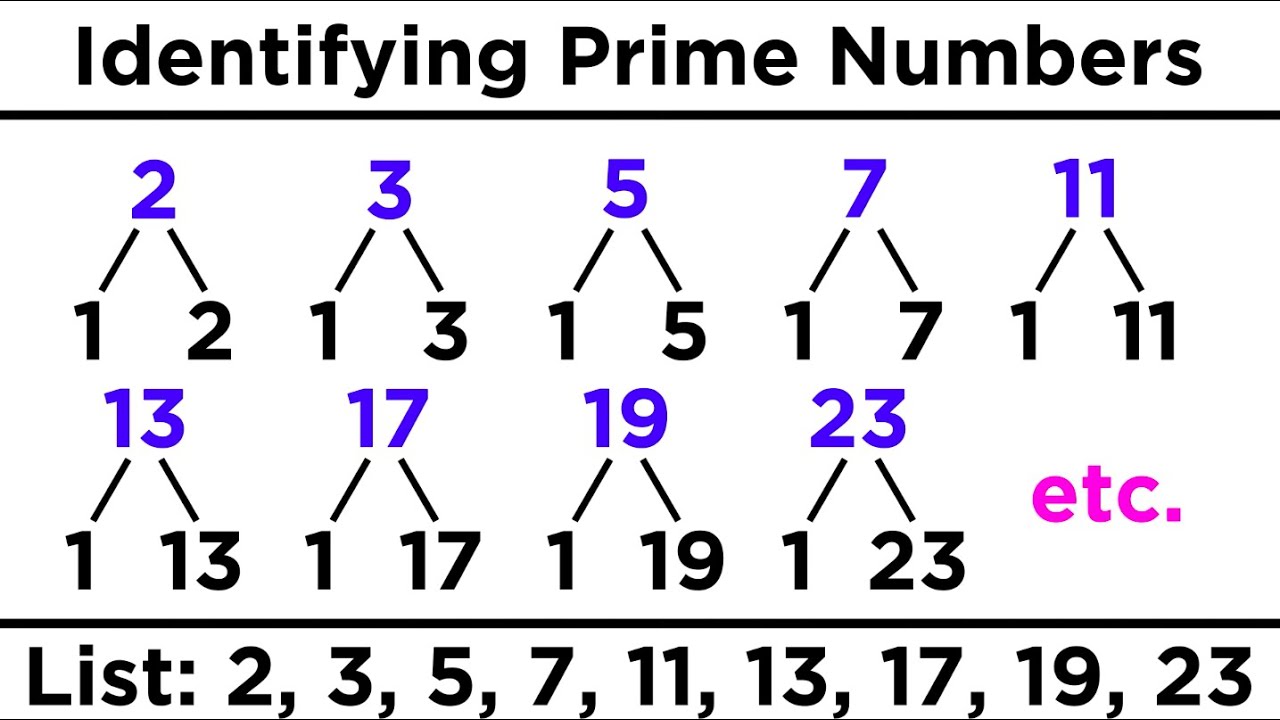
- 🚫 A 'simple' test is mentioned for determining which numbers cannot be drawn as squares: if a number has a prime factor of the form (4k+3) raised to an odd power, it cannot be expressed as the sum of two squares.
- 🔍 The script suggests using a computer program to exhaustively check which numbers can and cannot be drawn as squares on the grid, indicating that this is a complex problem.
- 📚 The video script ends with a promotion for Brilliant.org, suggesting that it is a resource for learning more about number theory and other mathematical concepts.
- 🎥 The script is from a video that also previews the next topic, which will be about the approximation of Pi by the ratio 22/7 and its significance.
Q & A
What is the area of a 4 by 4 square drawn on a dotty paper?
-The area of a 4 by 4 square is 16 square units, as the area of a square is calculated by multiplying the length of one side by itself.
Why are the areas of the squares drawn on the dotty paper always square numbers?
-The areas are square numbers because the squares are being drawn with sides of equal length, and the area of a square is calculated as side length squared (s^2), which naturally results in a square number.
What is the area of a square drawn on the grid that is not a square number?
-A square that is not a square number can still be drawn on the grid by using diagonals or slanted lines, but its area can be calculated using the formula a^2 + b^2, where 'a' and 'b' are the horizontal and vertical distances from the starting point to the opposite corner of the square.
How did the conversation lead to a discussion about Pythagorean theorem?
-The discussion about the area of slanted squares on the grid naturally led to the Pythagorean theorem because the area calculation for these shapes involves the sum of squares of the horizontal and vertical distances, which is the essence of the theorem.
What is the significance of the (a, b) notation in the context of the script?
-The (a, b) notation represents the horizontal and vertical distances used to draw slanted squares on the grid. It helps in identifying the pattern and calculating the area of these shapes without having to draw them.
Why can't a square with an area of 3 be drawn on the dotty paper?
-A square with an area of 3 cannot be drawn because 3 cannot be expressed as the sum of two square numbers, which is a requirement for drawing such shapes on the grid using the given method.
What is the mathematical concept that determines which numbers can be drawn as squares on the dotty paper?
-The mathematical concept is related to number theory, specifically which integers can be expressed as the sum of two squares.
What is the condition for a number to be unable to be expressed as the sum of two squares?
-A number cannot be expressed as the sum of two squares if it has a prime factor of the form (4k+3) raised to an odd power.
How does the script connect the problem of drawing squares on dotty paper to advanced number theory?
-The script connects the problem by showing that determining which areas can be drawn as squares on the dotty paper is equivalent to finding which numbers can be expressed as the sum of two squares, a classic problem in number theory.
What is the educational value of the problem presented in the script?
-The problem of drawing squares on dotty paper has educational value as it introduces concepts of geometry, algebra, and number theory in a循序渐进 and accessible way, leading to deeper mathematical understanding.
Outlines
🎨 Drawing Squares on Dotty Paper
The script begins with a discussion about drawing squares on a grid using dots as a guide. The conversation explores the concept of square numbers and how they relate to the area of the squares that can be drawn. It also introduces the idea of drawing non-square number areas by using diagonals or 'slanty squares'. The challenge is to determine which areas can be achieved on the grid, leading to the discovery that some numbers, like 3, cannot be represented as the sum of two squares, hinting at a deeper mathematical principle.
📚 Uncovering Mathematical Patterns and Pythagorean Proof
This paragraph delves deeper into the mathematical implications of the drawing activity. It introduces the concept of a 'slanty square' and its relation to the Pythagorean theorem. The script explains how the area of such a slanty square can be calculated using the formula a squared plus b squared, where 'a' and 'b' represent the horizontal and vertical distances, respectively. The discussion also highlights an unexpected proof of Pythagoras' theorem that emerges from this grid-based problem, showcasing the interconnectedness of mathematical concepts.
🔍 Advanced Number Theory and the Sum of Two Squares
The final paragraph elevates the discussion to the realm of number theory, focusing on which numbers can be expressed as the sum of two squares. It presents a test involving prime factors of the form (4k+3) to determine if a number can be drawn as a square on the grid. The script points out that numbers with such prime factors to an odd power cannot be represented as the sum of two squares, thus they cannot be drawn. The conversation also touches on the complexity of this problem and its place in higher-level mathematics, suggesting further exploration for those interested in number theory.
Mindmap
Keywords
💡Square
💡Area
💡Grid
💡Dotty Paper
💡Square Numbers
💡Pythagorean Theorem
💡Right-Angled Triangle
💡Number Theory
💡Prime Numbers
💡Sum of Two Squares
💡Exhaustion
Highlights
The concept of drawing squares on a dotty paper and determining their sizes leads to a discussion on square numbers and areas.
A 4 by 4 square has an area of 16 square units, introducing the idea of square numbers in terms of area.
The exploration of other possible square sizes on a grid, adhering to the rule of using dots and straight lines.
The realization that only square numbers can be drawn as squares on the grid, leading to a deeper investigation.
The introduction of the idea of 'slanty squares' and the challenge of drawing non-square number areas.
The creative approach to drawing a 'two-four' square by going diagonally, demonstrating the flexibility of the grid.
The calculation of the area of the 'two-four' square, showcasing a method to determine areas of non-square numbers.
The discovery that some numbers, like 3, cannot be drawn as squares on the grid, despite allowing diagonals.
The successful drawing of a square with an area of 5 using a diagonal approach, illustrating problem-solving in geometry.
The transition from geometry to number theory, as the problem evolves into which numbers can be expressed as the sum of two squares.
The introduction of the (a,b) notation to represent slanty squares and the algebraic method to calculate their areas.
The proof of Pythagoras' theorem that emerges from the algebraic expression for the area of slanty squares.
The revelation that numbers with a prime factor of the form (4k+3) to an odd power cannot be drawn as squares on the grid.
The practical application of the theory to identify numbers that cannot be drawn as squares, such as 3, 6, 7, and 11.
The discussion on the complexity of number theory and its relevance to the simple problem of drawing squares on dotty paper.
The promotion of Brilliant.org as a resource for learning more about number theory and other mathematical concepts.
The teaser for the next video about the approximation of Pi and its historical significance in mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: