believe in the math, not wolframalpha

blackpenredpen
17 Aug 201714:49
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a complex mathematical problem involving cube roots and square roots, which the presenter aims to solve without a calculator using Wolfram Alpha. Through a step-by-step process, the presenter simplifies the expression by raising both sides to the third power and applying the binomial theorem. After a series of algebraic manipulations, the solution is found to be a real number, x equals 2, which simplifies the original expression to just the number 2. The presenter also discusses the possibility of finding complex solutions using polynomial division and the quadratic formula, but emphasizes the real answer. The script concludes with a comparison of the solution to Wolfram Alpha's output, suggesting that sometimes manual calculations can be more reliable.

Takeaways
  • 🧐 The video is a math tutorial focusing on solving a complex expression involving square roots and cube roots without using a calculator.
  • 📚 The presenter introduces the problem and encourages viewers to pause and attempt the problem before revealing the solution.
  • 🔍 The problem involves simplifying an expression with nested roots and cannot be simplified by direct cancellation due to the nature of the roots.
  • 📈 The presenter uses the binomial theorem and Pascal's triangle to expand and simplify the expression raised to the third power.
  • 📝 The process involves carefully raising each part of the expression to the third power and combining like terms.
  • 🤔 The presenter simplifies the expression step by step, focusing on the middle terms which are more complex to handle.
  • 🔢 The presenter identifies that certain terms cancel out, simplifying the expression significantly.
  • 📉 The video demonstrates the use of algebraic manipulation to solve for 'x' by setting up an equation and isolating the variable.
  • 🎯 The solution to the problem is found to be x = 2, which means the original complex expression simplifies to the number 2.
  • 🤖 The presenter mentions using Wolfram Alpha to check the solution but finds a discrepancy in the results, suggesting that sometimes even computational tools can provide incorrect answers.
  • 📊 The video concludes with a reminder to trust mathematical reasoning over computational tools when discrepancies arise.
Q & A

  • What is the main problem presented in the video?

    -The main problem is to simplify and find the value of a complex expression involving square roots and cube roots.

  • Why can't the terms with square roots be canceled out in the expression?

    -The terms with square roots cannot be canceled out because they are not like terms; they have different radicands (the numbers under the root).

  • What mathematical concept is used to simplify the cube root terms?

    -The concept of raising a power to a power is used, specifically raising the expression to the third power to eliminate the cube root.

  • What is the significance of using Pascal's triangle in this context?

    -Pascal's triangle is used to expand the binomial (a + b) raised to the third power, which is part of the process to simplify the expression.

  • How does the video demonstrate the process of solving the expression?

    -The video demonstrates by setting the expression equal to a variable X, then raising both sides to the third power and simplifying step by step.

  • What is the role of the binomial theorem in solving the problem?

    -The binomial theorem is used to expand the expression when a binomial is raised to the third power, which helps in simplifying the expression further.

  • What is the final answer to the simplified expression?

    -The final answer to the simplified expression is the number 2.

  • Why does the video mention Wolfram Alpha and then later express doubt about its result?

    -The video mentions Wolfram Alpha to show an alternative method of solving the problem, but later expresses doubt because the result from Wolfram Alpha did not match the simplified answer of 2 obtained through manual calculations.

  • What is the importance of checking for real roots in the context of this problem?

    -The importance of checking for real roots is because the problem involves cube roots, which must be real numbers to have a meaningful solution.

  • How does the video handle the possibility of complex solutions?

    -The video acknowledges the possibility of complex solutions but focuses on finding the real solution, which is the primary goal of the problem presented.

  • What is the final step in verifying the solution found in the video?

    -The final step is to substitute the found solution (X = 2) back into the original expression to see if it simplifies correctly, confirming the solution.

Outlines
00:00
🤔 Introduction to the Problem

The speaker challenges the viewer with a math problem involving cube roots and square roots, promising a detailed solution using mathematical principles without a calculator.

05:02
🧮 Detailed Solution Approach

The speaker explains the process of raising both sides of the equation to the third power, using binomial expansion and Pascal's triangle to simplify the expression. They identify terms that cancel out and reveal how to handle remaining complex terms.

10:02
📏 Simplification and Result Verification

The speaker continues simplifying the equation, factoring out common terms, and determining that the expression equals 2. They demonstrate verifying this solution using the rational root theorem and hint at potential complex solutions.

Mindmap
Keywords
💡Wolfram Alpha
Wolfram Alpha is a computational knowledge engine or answer engine that computes answers to mathematical, statistical, and other types of questions. In the video, the presenter mentions using Wolfram Alpha to solve a complex mathematical problem, indicating its utility in providing solutions to complex queries without the need for manual calculation.
💡Cube Root
A cube root is a value that, when cubed, gives the original number. In the video, the cube root is a fundamental concept used in simplifying the given mathematical expression. The script discusses raising expressions to the power of one-third to deal with cube roots, demonstrating the process of simplifying complex roots.
💡Square Root
A square root is a value that, when squared, equals the original number. The video script involves square roots within the context of a complex expression that the presenter is trying to simplify. The square root is used in conjunction with cube roots to form the basis of the mathematical problem.
💡Binomial Theorem
The Binomial Theorem provides a way to expand expressions of the form (a + b)^n. In the script, the presenter references the theorem when raising a binomial to the third power, using it to expand the expression and simplify the problem step by step.
💡Pascal's Triangle
Pascal's Triangle is a triangular array of numbers where each number is the sum of the two numbers directly above it. The video mentions Pascal's Triangle as a method to expand (a + b)^3, which is relevant to the cube root simplification process.
💡Complex Numbers
Complex numbers are numbers that consist of a real part and an imaginary part. The script mentions the possibility of finding complex values for the expression, indicating that while the focus is on real solutions, the mathematical process can also accommodate complex numbers.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. In the video, the presenter eventually arrives at a polynomial equation that needs to be solved to find the value of x.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of its factors. The script describes factoring out a common term, in this case, -3, from the polynomial equation to simplify the process of finding the solution for x.
💡Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax^2 + bx + c = 0. Although the video focuses on finding a real solution, the script mentions that after factoring, one could use the quadratic formula to find complex solutions if needed.
💡Real Number
A real number includes all the numbers that can be found on the number line, including integers, fractions, and irrational numbers. The video emphasizes finding a real number solution for the cube root expression, which is a key part of the problem-solving process.
💡Calculator
A calculator is an electronic device used to perform arithmetic operations. The script humorously mentions not using a calculator for the problem at hand, instead opting for a step-by-step manual solution to demonstrate the mathematical process.
Highlights

Introduction of a complex mathematical problem involving square roots and cube roots without using a calculator.

Use of Wolfram Alpha to demonstrate the solution process.

Explanation of the mathematical approach to simplify the expression by raising both sides to the third power.

Introduction of the binomial theorem and Pascal's triangle for expanding expressions.

Step-by-step calculation of the expression using cube roots and square roots.

Cancellation of terms in the equation to simplify the expression further.

Multiplication of terms inside the cube root to simplify the equation.

Use of the difference of squares formula to simplify the equation.

Identification of potential rational solutions by checking factors of 14.

Verification of the solution x = 2 by substituting back into the equation.

Explanation of the process to find complex solutions using polynomial division and the quadratic formula.

Comparison of the manual solution with Wolfram Alpha's result, highlighting discrepancies.

Emphasis on trusting mathematical intuition over computational tools in some cases.

Final confirmation that the original expression simplifies to the number 2.

Discussion on the importance of understanding the mathematical process over relying solely on calculators.

Encouragement for viewers to verify the solution independently using their own methods.

Concluding remarks on the value of mathematical exploration and problem-solving.

Transcripts

Browse More Related Video

Exponential Equations With Powers of X

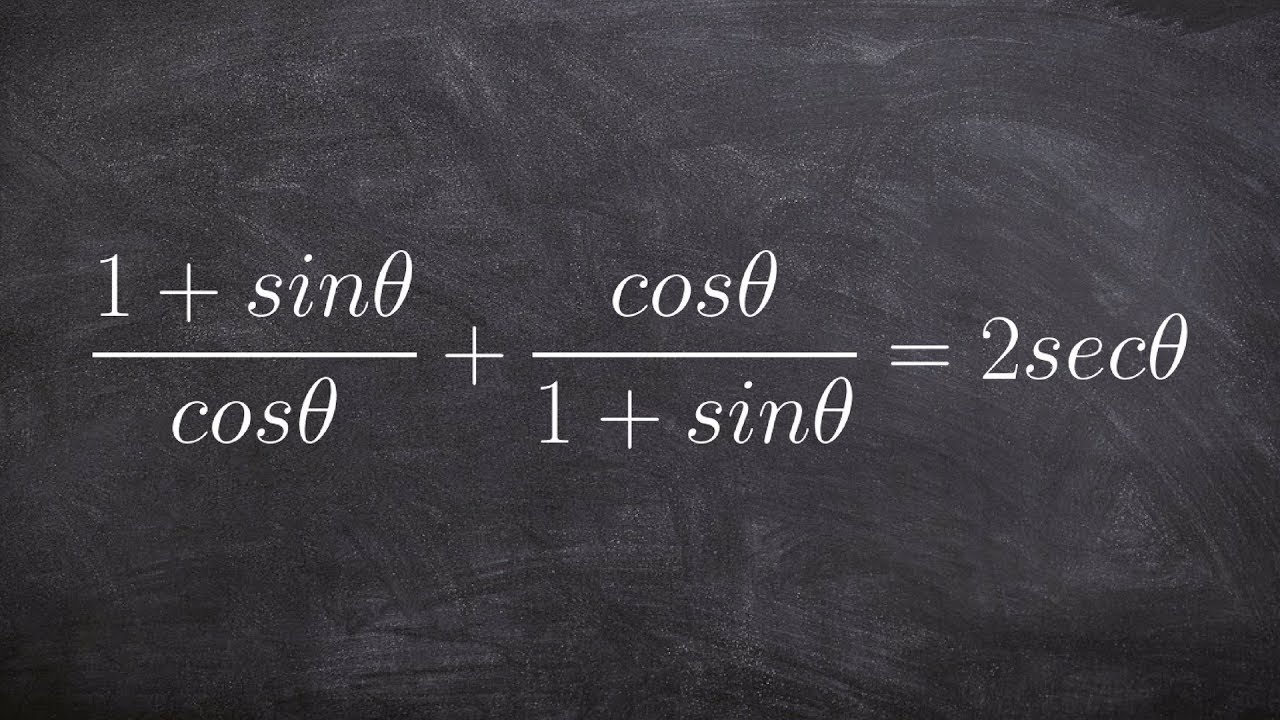
Verifying a trigonometric Identities

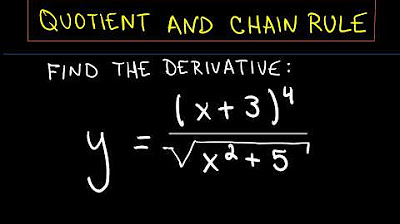
Derivatives - Quotient and Chain Rule and Simplifying

A Limit Example Combining Multiple Algebraic Tricks

How to solve a quadratic equation with Casio fx-991MS edition 2 scientific calculator

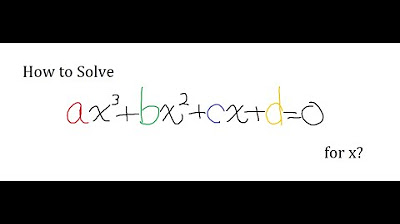
[Algebra] Is there any cubic formula?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Math ProblemRoots CalculationBinomial TheoremPascal's TriangleWolfram AlphaAlgebraic SolutionEducational ContentComplex NumbersReal NumbersPolynomial Equation