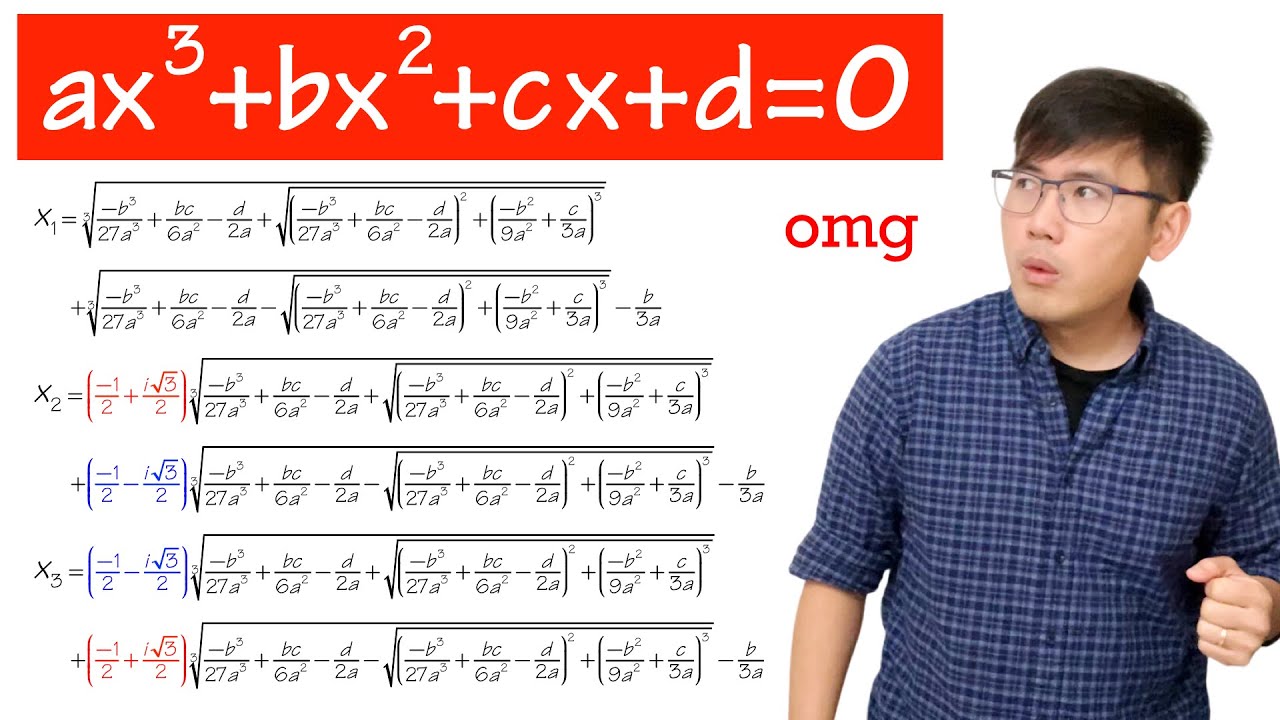[Algebra] Is there any cubic formula?
TLDRIn this educational video, the presenter delves into solving cubic equations using Cardano's Formula. Starting with the general cubic expression \( ax^3 + bx^2 + cx + d = 0 \), the video explains the importance of the leading coefficient 'a' being non-zero. The presenter guides through a series of algebraic manipulations, including a substitution to eliminate the \( x^2 \) term, leading to a depressed cubic equation. The method then introduces new variables \( u \) and \( v \) to transform the equation into a solvable form, ultimately using the quadratic formula to find the roots. The video concludes with the general solution for one root of the cubic equation, promising a continuation for the remaining roots in a follow-up video.
Takeaways
- 📚 Yesterday's lesson covered inequalities of rational functions and involved factoring a cubic polynomial.
- 🔍 Today, the focus is on solving cubic polynomials in general, starting with the expression a*x^3 + b*x^2 + c*x + d = 0, where a, b, c, and d are real numbers, and a ≠ 0.
- ✏️ If a were 0, the equation would reduce to a quadratic, simplifying the problem.
- 🔢 The goal is to find a general solution for cubic polynomials using the Cardano formula, developed by the Italian mathematician Cardano.
- 📉 The method involves converting the cubic equation to one without an x^2 term by substituting x with x + b/3a.
- 🧮 Cardano's formula simplifies to u + v = x and involves complex substitutions and factorization to reduce the equation.
- 💡 The process involves setting u and v to represent parts of the polynomial and then solving for x.
- 🔄 The solution for x is derived by finding the cube roots of the substituted values and combining them appropriately.
- 📖 Today's session covers the derivation of the first solution, with plans to explore the remaining two solutions in future lessons.
- 📝 The final general solution for the cubic equation is given as x = -b/3a + (u + v), where u and v are specific values derived from the polynomial.
Q & A
What was the main topic discussed in the video?
-The main topic discussed in the video was finding the roots of a cubic polynomial and introducing Cardano's formula as a method to solve any general cubic equation.
Why is it necessary for 'a' to be non-zero in the cubic polynomial equation?
-'a' must be non-zero because it is the leading coefficient. If 'a' were zero, the term involving 'x cubed' would disappear, reducing the equation to a quadratic one instead of a cubic.
What is the general form of a cubic polynomial equation discussed in the video?
-The general form of the cubic polynomial equation discussed is ax^3 + bx^2 + cx + d = 0, where 'a', 'b', 'c', and 'd' are real numbers and 'a' is not equal to zero.
Why did Cardano's formula initially only provide real solutions?
-Cardano's formula initially only provided real solutions because the concept of complex numbers was not developed during his time, and thus people were not aware of the existence of complex numbers.
What substitution is used to eliminate the x squared term in the cubic equation?
-The substitution used to eliminate the x squared term is letting X (capital x) be equal to x plus b/(3a), which helps to degenerate the cubic polynomial into a form without an x squared term.
What is the purpose of the substitution u + v = X in Cardano's method?
-The purpose of the substitution u + v = X is to transform the depressed cubic equation into a form that allows for the application of Cardano's formula, making it easier to solve for the roots.
What are the two equations derived from the substitution u + v = X in Cardano's method?
-The two equations derived are u^3 + v^3 + q = 0 and 3uv + p = 0, where 'p' and 'q' are expressions involving the original coefficients of the cubic polynomial.
How does Cardano's formula relate to the quadratic formula?
-Cardano's formula relates to the quadratic formula in that it uses a similar approach of substituting and simplifying the original equation to a form that can be solved more easily, although it applies to cubic equations.
What is the final form of the solution for the cubic equation using Cardano's method?
-The final form of the solution for the cubic equation using Cardano's method is x = -b/(3a) + u and x = -b/(3a) + v, where 'u' and 'v' are the cube roots of specific expressions derived from the original cubic equation.
What is the significance of the commutative property in the context of the final solution for the cubic equation?
-The commutative property signifies that the order of 'u' and 'v' in the final solution does not matter, as they are interchangeable due to the addition operation, which simplifies the process of finding the roots.
Outlines
📚 Introduction to Solving Cubic Polynomials
The video script begins with a recap of the previous session on inequalities of rational functions, highlighting the challenge of solving a cubic polynomial that couldn't be easily factored with integer coefficients. The speaker introduces the general form of a cubic polynomial (ax^3 + bx^2 + cx + d = 0) and sets the stage for discussing the Cardano formula, a method developed by the Italian mathematician Cardano to solve cubic equations. The importance of the leading coefficient 'a' is emphasized, as it cannot be zero, and the video promises to explore the derivation of the formula and its application to find the roots of cubic polynomials.
🔍 Depress the Cubic Polynomial to Eliminate the x^2 Term
In this paragraph, the focus is on the process of 'depressing' the cubic polynomial to remove the x^2 term, similar to the approach used in the quadratic formula. The substitution x = X - b/(3a) is introduced to simplify the equation. The script details the algebraic manipulations involved in this process, including cubing the substitution, expanding, and simplifying the terms to achieve a new polynomial without an x^2 term. The resulting equation is then rearranged to prepare for further substitution and simplification.
🎯 Substitution and Grouping Terms for Cardano's Method
The script continues with Cardano's method by introducing a new substitution where u and v are variables that sum up to X (capital x). The goal is to express the equation in terms of u and v to facilitate solving. The speaker elaborates on how to group terms to factor out (u+v) and simplify the equation into a form that can be solved using the quadratic formula. The process involves expanding the cube of the sum (u+v) and carefully grouping terms to isolate the x^2 and x terms, leading to a system of equations that can be solved for u and v.
🧩 Solving the System of Equations for u and v
The speaker presents a system of equations derived from the previous steps, which includes u^3 + v^3 + q = 0 and 3uv + p = 0. The task is to solve for u and v, which are related to the original variable x through the sum X. The script explains the process of rewriting these equations and introducing new variables U and V, which are the cubes of u and v, respectively. This transformation leads to a quadratic equation in terms of z, which can be solved using the quadratic formula, providing a pathway to find the values of u and v.
🏁 Deriving the General Solution for the Cubic Equation
In the final paragraph, the script concludes with the derivation of the general solution for the cubic equation. The speaker uses the quadratic formula to solve for z, which leads to finding the values of u and v. The solution involves taking the cube roots of certain expressions and substituting back to find the values of x. The script emphasizes that the solution is general and can be applied to any cubic equation, and it concludes with the promise of a follow-up video to discuss the remaining solutions.
Mindmap
Keywords
💡Inequalities of Rational Functions
💡Cubic Polynomial
💡Cardano's Formula
💡Leading Coefficient
💡Quadratic Equation
💡Substitution
💡Depressed Cubic
💡Complex Numbers
💡Quadratic Formula
💡Commutative Property
Highlights
Introduction to solving inequalities of rational functions and the challenge of finding roots of cubic polynomials.
Assumption that coefficients a, b, c, d are real numbers, with a not equal to zero as the leading coefficient.
Explanation of why a cannot be zero and the implications for the polynomial's degree.
Discussion on simplifying the problem when d equals zero, leading to a linear and quadratic factor.
Introduction of Cardano's formula for finding a general solution for cubic equations.
Historical context of Cardano's work and the absence of complex numbers in his era.
The method of degrading the cubic polynomial to eliminate the x squared term.
Substitution of x with (x + b/(3a)) to simplify the cubic equation.
Derivation of the depressed cubic equation after substitution.
Introduction of new variables u and v to further simplify the equation.
Formation of a system of equations with u and v representing x.
Transformation of the system into a quadratic equation in terms of z.
Application of the quadratic formula to solve for z, which represents u and v.
Explanation of the commutative property allowing for interchangeable u and v values.
Final derivation of the general solution for the cubic equation using Cardano's method.
Promise of a follow-up video to discuss the remaining two solutions.
Conclusion and sign-off, with an invitation to the next video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: