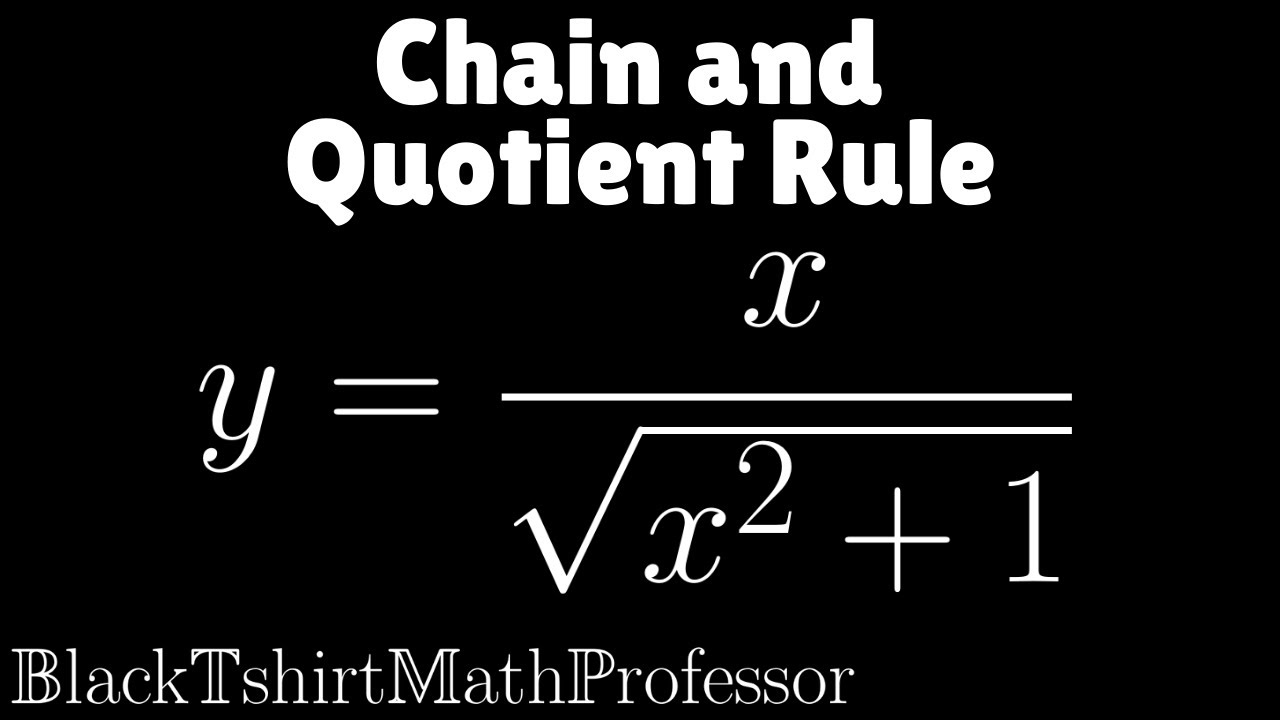Derivatives - Quotient and Chain Rule and Simplifying

patrickJMT
21 Nov 200807:10
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter demonstrates the process of finding the derivative of a complex function using both the quotient and chain rules. The function given is y = (x + 3)^4 / (sqrt(x)^2 + 5). The video walks through rewriting the square root as a power, applying the quotient rule, and simplifying the expression step by step. The presenter also explains the importance of factoring and the use of the discriminant to determine if the polynomial can be factored further, ultimately leaving the final simplification as an exercise for the viewers.

Takeaways
  • 📘 The video demonstrates how to derive a function using the quotient and chain rules.
  • 🧮 The given function is y = (x + 3)^4 / sqrt(x^2 + 5).
  • 🔄 The square root in the denominator is rewritten as (x^2 + 5)^(1/2) to facilitate the use of the chain rule.
  • 📏 The quotient rule is applied: the bottom times the derivative of the top minus the top times the derivative of the bottom, all over the bottom squared.
  • 📝 The derivative of the top (x + 3)^4 is calculated using the chain rule: 4(x + 3)^3.
  • ⚖️ The derivative of the bottom (x^2 + 5)^(1/2) is also calculated using the chain rule: (1/2)(x^2 + 5)^(-1/2) * 2x.
  • 🔍 The function's simplified form after applying the quotient rule involves combining and simplifying terms carefully.
  • 📊 Factoring out common terms from the numerator and simplifying the denominator is essential for further simplification.
  • 🔗 The expression (x^2 + 5)^(1/2) is moved to the denominator to simplify the final expression.
  • ✅ The final simplified form of the derivative is presented, along with an explanation that further factorization using the discriminant shows it cannot be simplified with real numbers.
Q & A

  • What is the function y being simplified in the video?

    -The function y is given as the quotient of (x + 3) to the fourth power and the square root of x squared plus five.

  • Why is the square root rewritten as a power of one-half in the video?

    -The square root is rewritten as a power of one-half to simplify the application of the chain rule in the derivative process.

  • What is the quotient rule mentioned in the video for differentiation?

    -The quotient rule states that the derivative of a fraction is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.

  • How is the chain rule applied to the top part of the function in the video?

    -The chain rule is applied by taking the derivative of the outer function (raising to the power of 4) and multiplying it by the derivative of the inner function (x), while also adjusting for the power.

  • What is the derivative of the bottom part of the function in the video?

    -The derivative of the bottom part involves taking the derivative of x squared plus five to the power of one-half, which results in multiplying by the power of negative one-half and the derivative of the inner function, which is 2x.

  • What simplification is made with the powers of x squared plus five in the denominator?

    -The simplification involves recognizing that the 1/2 and 2 in the denominator cancel each other out, leaving x squared plus five.

  • What is the significance of factoring out the smaller power in the terms with x squared plus five and x plus three?

    -Factoring out the smaller power helps to simplify the expression and makes it easier to combine like terms and further simplify the derivative.

  • How does the video handle the simplification of the expression inside the brackets?

    -The video moves terms from the numerator to the denominator, adjusts the exponents accordingly, and simplifies the expression by combining like terms.

  • What is the discriminant test mentioned in the video, and why is it relevant?

    -The discriminant test (b squared - 4ac) is used to determine whether a quadratic equation has real solutions. It is relevant to check if the simplified expression can be factored further.

  • Why does the video suggest that the final expression might not factor further with real numbers?

    -The video suggests that the discriminant would result in a negative number, indicating that the quadratic expression does not have real roots and thus cannot be factored further with real numbers.

  • What advice does the video give to the viewers regarding the derivative presented?

    -The video advises viewers to practice the steps and consider the simplification process as an exercise, encouraging them to explore whether the expression can be factored further.

Outlines
00:00
📚 Derivative Calculation Using Quotient and Chain Rules

This paragraph introduces a mathematical tutorial on calculating the derivative of a function using the quotient and chain rules. The function given is y = (x + 3)^4 / (√(x^2 + 5)). The process starts by rewriting the square root as a power of one-half to simplify the application of the chain rule. The quotient rule is then explained, which involves differentiating the numerator and denominator separately and combining the results. The chain rule is applied to the numerator, factoring out constants and simplifying the expression. The paragraph concludes with the intermediate steps of the derivative calculation, emphasizing the importance of correctly applying the rules and simplifying the result.

05:08
🔍 Completing the Derivative and Simplification Exercise

The second paragraph continues the derivative calculation from the first, focusing on completing the process and simplifying the expression. The speaker moves terms from the numerator to the denominator, adjusts exponents, and simplifies the polynomial within the derivative. They discuss the possibility of the polynomial factoring further and use the discriminant to determine if it can be factored with real numbers. The conclusion is that the polynomial does not factor further, and the final simplified form of the derivative is presented. The paragraph ends with an invitation for viewers to engage with the content by asking questions and comments, and a hope that the tutorial is clear and helpful.

Mindmap
Keywords
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. In the video, the derivative is the main focus, as the instructor demonstrates how to find the derivative of a given function using both the quotient and chain rules. The term is central to the video's theme of teaching calculus concepts.
💡Quotient Rule
The quotient rule is a fundamental calculus formula used to find the derivative of a quotient of two functions. The video script describes its application in the context of simplifying the given function by first rewriting the square root as a power, then applying the quotient rule to differentiate the function. It's a key step in the process demonstrated in the video.
💡Chain Rule
The chain rule is another essential calculus principle used to differentiate composite functions. The script mentions using the chain rule to simplify the derivative of the top part of the quotient. It's a critical component in the video's explanation of how to break down and differentiate complex functions.
💡Square Root
A square root is a mathematical operation that finds a number which, when multiplied by itself, gives the original number. In the video, the square root is rewritten as a power to facilitate the application of the chain rule. It's an example of simplifying expressions in calculus to make differentiation more manageable.
💡Power
In mathematics, a power refers to the result of multiplying a number by itself a certain number of times. The script uses powers to rewrite the square root and to simplify the expression during differentiation. Powers are integral to the process of differentiating functions involving roots or exponents.
💡Simplification
Simplification in calculus involves reducing complex expressions to a more manageable form. The video script emphasizes the importance of simplification after applying differentiation rules to make the resulting expression easier to understand and work with. It's a recurring theme in the video as the instructor simplifies the derivative step by step.
💡Factoring
Factoring is the process of breaking down a polynomial or expression into a product of its factors. In the script, the instructor factors out common terms to simplify the derivative further. Factoring is a common technique used in algebra and calculus to simplify expressions and solve equations.
💡Discriminant
The discriminant is a part of the quadratic formula used to determine the nature of the roots of a quadratic equation. In the video, the instructor mentions the discriminant in the context of determining whether a polynomial can be factored further. It's a brief mention but highlights an important concept in algebra that is related to the differentiation process.
💡Exponents
Exponents are used to denote repeated multiplication of a number by itself a certain number of times. The script discusses exponents in the context of differentiating functions with powers, such as 'x to the fourth' and 'x squared plus five to the one-half power'. Exponents are a key part of the calculus process shown in the video.
💡Differentiation
Differentiation is the process of finding the derivative of a function. The entire video is a tutorial on differentiation, showing step-by-step how to apply the quotient and chain rules to find the derivative of a given function. Differentiation is the overarching theme of the video, with each step contributing to the final derivative.
💡Polynomial
A polynomial is an algebraic expression made up of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The script refers to polynomials when discussing the derivative of the function, as the function itself is a polynomial. Polynomials are a common subject of differentiation in calculus.
Highlights

The video demonstrates how to use the quotient and chain rules to find the derivative of a given function.

Rewriting the square root as a power for easier application of the chain rule.

Explanation of the quotient rule: bottom times the derivative of the top minus the top times the derivative of the bottom, all over the bottom squared.

Using the chain rule to find the derivative of the top part of the function.

Simplifying the expression by factoring out common terms.

Multiplying out and simplifying the remaining expression after applying the quotient rule.

Factoring out the smaller power of common terms to simplify the function further.

Combining and simplifying the exponents of the terms in the numerator and denominator.

Distributing and combining like terms within the simplified expression.

Determining that the polynomial inside the brackets cannot be factored further using the discriminant.

Final simplified form of the derivative after all algebraic manipulations.

Explanation of each step in the simplification process, ensuring clarity and understanding.

Mention of potential errors and the importance of double-checking work to avoid missing exponents.

Encouragement to viewers to practice and apply the techniques discussed in the video.

Invitation to viewers to post questions and comments for further clarification.

Transcripts

Browse More Related Video

Chain Rule with the Quotient Rule Problem 3 (Calculus 1)

DERIVATIVE OF RADICAL: THE CHAIN RULE

Second Derivative of Implicit Function

How to take the derivative with chain rule inside product rule

Rules of Logs | MIT 18.01SC Single Variable Calculus, Fall 2010

Simplifying Derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Derivative CalculationQuotient RuleChain RuleMathematics TutorialSimplification TechniquesEducational ContentMath VideoCalculus ConceptsAlgebraic ManipulationDiscriminant Factor