10.1.1 Correlation - Linear, Nonlinear, Positive Linear, and Negative Linear Correlation Defined
TLDRThis video script introduces key terminology related to scatter plots and correlation, including definitions of scatter plot, correlation, linear correlation, and the linear correlation coefficient. It explains how to interpret scatter plots to infer correlations between variables, distinguishing between positive, negative, and non-linear relationships. The script also touches on the subjectivity of visual analysis and the use of hypothesis testing to provide a more concrete assessment of linear correlation, with the linear correlation coefficient 'r' serving as a sample statistic for such tests.
Takeaways
- 📊 The video focuses on defining key terms related to scatter plots and correlation, including 'scatter plot', 'correlation', 'linear correlation', and 'linear correlation coefficient'.
- 📈 The instructor does not demonstrate how to create a scatter plot in this video, instead referring viewers to homework help videos for Excel tutorials.
- 👤 The purpose of the video is to help viewers understand how to define important terms and interpret scatter plots to infer the presence of a correlation between two variables.
- 📈 A scatter plot is a graphical representation of a set of ordered pairs, typically plotting the first variable on the x-axis and the second on the y-axis.
- 🔍 The concept of 'correlation' in statistics refers to a relationship between two variables, which can be identified by a pattern in the scatter plot.
- ➡️ 'Linear correlation' suggests that the data points appear to lie on a straight line, indicating either an increase or decrease in both variables.
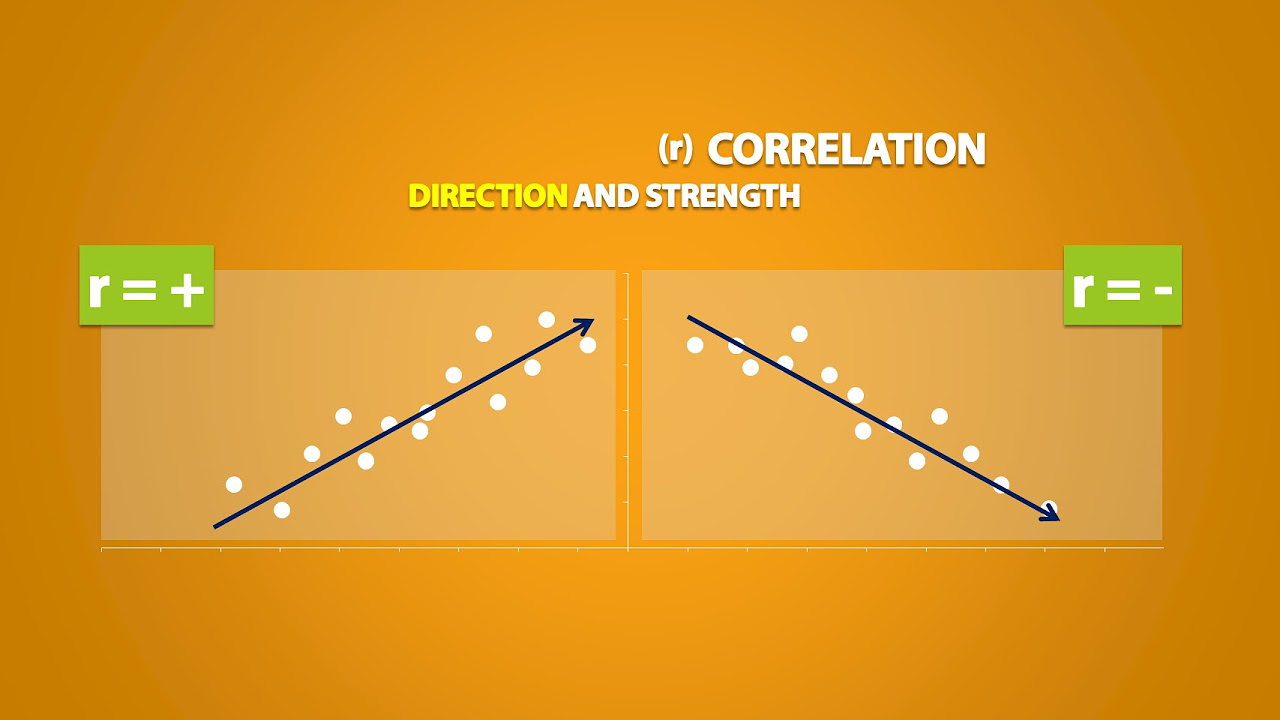
- ⬆️ 'Positive linear correlation' occurs when both variables increase together, while 'negative linear correlation' occurs when one variable increases as the other decreases.
- 📊 The video provides examples of scatter plots that show both linear and non-linear relationships, including one with no apparent correlation.
- 📉 The 'linear correlation coefficient' (r) is a numerical value that measures the strength and direction of a linear relationship between two variables.
- 🧐 The video emphasizes the subjective nature of interpreting scatter plots but also mentions the use of hypothesis testing for a more objective analysis.
- 📚 The instructor plans to delve deeper into the linear correlation coefficient and hypothesis testing in a subsequent video.
Q & A
What is the primary focus of the video script?
-The primary focus of the video script is to define important terminology related to scatter plots and correlation, including terms like scatter plot, correlation, linear correlation, and linear correlation coefficient.
What does the instructor hope the viewers will be able to do by the end of the video?
-The instructor hopes that by the end of the video, viewers will be able to define the discussed terms and use a scatter plot to subjectively infer whether there is a correlation between two variables.
Why does the instructor not show how to construct a scatter plot in this video?
-The instructor does not show how to construct a scatter plot in this video because the focus is on the terminology and interpretation of scatter plots, not the technical construction. For instructions on constructing scatter plots, viewers are directed to the homework help videos.
What is the purpose of a scatter plot?
-The purpose of a scatter plot is to visually represent the relationship between two variables by plotting a set of ordered pairs, where one variable is on the x-axis and the other on the y-axis.
What does the term 'correlation' mean in the context of statistics?
-In statistics, 'correlation' refers to a relationship between two variables, indicating that there is a pattern or association between them.
How is a linear correlation different from a non-linear correlation?
-A linear correlation suggests that the paired data appears to lie on a straight line with a constant slope, whereas a non-linear correlation indicates a pattern that does not follow a straight line, such as a parabolic or exponential curve.
What does a positive linear correlation imply about the relationship between two variables?
-A positive linear correlation implies that as one variable increases, the other variable also increases, and the data points appear to lie on a straight line with a positive slope.
What does a negative linear correlation imply about the relationship between two variables?
-A negative linear correlation implies that as one variable increases, the other variable decreases, and the data points appear to lie on a straight line with a negative slope.
What is the purpose of the linear correlation coefficient (r)?
-The linear correlation coefficient (r) is a statistical measure that quantifies the strength and direction of a linear relationship between two variables, with values ranging from -1 to 1.
How can one confirm the presence of a correlation using hypothesis testing?
-One can confirm the presence of a correlation using hypothesis testing by examining the linear correlation coefficient (r) as a sample statistic and comparing it to the population parameter, the linear correlation coefficient rho, using either the critical value method or the p-value method.
What is the subjective aspect of interpreting scatter plots, and why is it recommended despite its subjectivity?
-The subjective aspect of interpreting scatter plots involves visually assessing the pattern of data points to determine if there appears to be a correlation and its direction. It is recommended because it provides a quick and initial analysis to reveal the presence of a correlation, which can then be confirmed through more objective statistical methods.
Outlines
📊 Understanding Scatter Plots and Correlation Terminology
This paragraph introduces the key concepts of scatter plots and correlation in statistics. It discusses the importance of defining terms such as 'scatter plot', 'correlation', 'linear correlation', and 'linear correlation coefficient'. The speaker aims to help viewers understand how to construct a scatter plot, typically using tools like Excel, and how to interpret these plots to infer if there is a correlation between two variables. An example is given using waist and arm circumference data to illustrate how a scatter plot can show a relationship between variables, suggesting a correlation when there is a discernible pattern. Definitions of correlation, linear correlation, and the distinction between positive and negative linear correlations are provided, along with an explanation of how the slope of the plotted points can indicate the direction of the correlation.
🔍 Analyzing Linear and Non-Linear Correlations in Scatter Plots
The second paragraph delves deeper into the analysis of linear and non-linear correlations depicted in scatter plots. It explains how to visually assess the presence of a linear correlation by observing the slope of the plotted points' pattern. The paragraph contrasts positive and negative linear correlations with examples, highlighting the significance of the slope direction in determining the type of correlation. Additionally, it addresses the subjective nature of interpreting scatter plots and introduces the concept of hypothesis testing to provide a more objective method for determining correlation. The paragraph also mentions the use of the linear correlation coefficient (r) and the population parameter (rho) in hypothesis testing, setting the stage for further discussion in subsequent videos. The importance of initial subjective analysis is emphasized as a quick method to identify potential correlations before applying more rigorous statistical tests.
Mindmap
Keywords
💡Scatter Plot
💡Correlation
💡Linear Correlation
💡Linear Correlation Coefficient
💡Positive Linear Correlation
💡Negative Linear Correlation
💡Non-linear Correlation
💡Ordered Pairs
💡Hypothesis Test
💡Critical Value Method
💡P-Value Method
Highlights
The video discusses defining key terminology related to scatter plots and correlation.
The aim is to enable viewers to define terms like scatter plot, correlation, linear correlation, and linear correlation coefficient.
The video does not demonstrate how to construct a scatter plot but focuses on interpreting them to infer correlation.
An example is provided using waist and arm circumference to illustrate the concept of correlation.
Scatter plots are graphs of ordered pairs, typically with the first variable on the x-axis and the second on the y-axis.
Correlation implies a relationship between two variables, which can be observed through a distinct pattern in plotted points.
Linear correlation suggests data points appear to lie on a straight line with a constant slope.
Positive linear correlation is identified when both variables increase together, forming a line with a positive slope.
Negative linear correlation occurs when one variable increases while the other decreases, forming a line with a negative slope.
An example of non-correlation is given, where data points are scattered without a distinct pattern, such as weight and pulse rate.
The linear correlation coefficient (r value) is introduced as a measure of the strength and direction of a linear relationship.
A high positive r value close to 1 indicates a strong positive correlation, while a high negative r value close to -1 indicates a strong negative correlation.
Non-linear correlations are identified by patterns that do not form a straight line, such as parabolic or exponential relationships.
The subjective nature of interpreting scatter plots is acknowledged, with the suggestion to use hypothesis tests for a more concrete analysis.
Hypothesis tests use the linear correlation coefficient (r) as the sample statistic and the population parameter rho for analysis.
Excel is recommended for constructing scatter plots, which will be demonstrated in the homework help videos.
The video concludes by emphasizing the importance of subjective analysis of scatter plots to quickly identify potential correlations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: