Correlation Doesn't Equal Causation: Crash Course Statistics #8

CrashCourse
14 Mar 201812:17
EducationalLearning
32 Likes 10 Comments

TLDRThis video explains relationships between variables in statistics. It discusses using scatter plots and correlation to measure and visualize linear relationships, explaining concepts like positive/negative correlation, regression lines, Pearson's analysis of father-son heights, and spurious correlations. It emphasizes that while correlation shows how variables move together, it does not prove causation. The video aims to provide viewers a better understanding of using correlation to describe data relationships.

Takeaways
  • 😀 Scatterplots are useful for visualizing relationships between two continuous variables
  • 😃 Linear relationships can be described using a regression line and correlation coefficient
  • 😄 Correlation measures the direction and closeness of the relationship between two variables
  • 😎 Positive correlation means two variables move in the same direction
  • 😕 Negative correlation means two variables move in opposite directions
  • 🤓 R-squared tells you how much variance in one variable can be predicted from the other variable
  • 😮 Correlation does not imply causation - just because two things are correlated does not mean one causes the other
  • 🤔 Spurious correlations can occur just by chance with no causal relationship
  • 😀 Looking at a scatterplot gives more insight into the relationship than just the correlation value
  • 💡 Understanding relationships between variables helps predict future events and reflect on past occurrences
Q & A

  • What are scatter plots useful for visualizing?

    -Scatter plots are useful for visualizing relationships between two continuous variables, also called bivariate data. They allow you to see the shape and spread of data in two dimensions.

  • How does a regression line help describe the relationship between two variables?

    -A regression line is a straight line that best fits the data points on a scatter plot. It allows you to make predictions about one variable based on the value of the other variable using the line's formula y=mx+b.

  • What does the slope (m) of a regression line tell you?

    -The slope (m) of a regression line tells you how much y changes for every 1 unit increase in x. It describes how strongly the two variables are related.

  • What does correlation measure?

    -Correlation measures how closely two variables move together, considering both the direction and closeness of their movement. It is represented by the correlation coefficient r.

  • How is the correlation coefficient r interpreted?

    -The sign of r (positive or negative) indicates whether the variables move in the same or opposite directions. The magnitude of r (closer to 1 or 0) indicates the strength of the linear relationship.

  • What does R-squared (R^2) represent?

    -R-squared (R^2) represents the proportion of variance in one variable that can be predicted from the other variable. It is between 0 and 1, with higher values indicating a better fit.

  • What is the difference between correlation and causation?

    -Correlation does not imply causation. Just because two variables are correlated does not mean that one causes the other. The relationship may be due to chance or a third confounding variable.

  • How can you identify spurious correlations?

    -Spurious correlations between very specific variables that seem unrelated are likely coincidental. Examining correlation together with causation and scatter plots helps avoid drawing false conclusions.

  • Why is it important to visualize data beyond just correlation?

    -Correlation statistics alone do not show the full picture. Scatter plots of the same correlated data can show very different relationships. Visualizing the data provides more insight.

  • What are some applications of understanding data relationships?

    -Understanding relationships allows us to predict events, reflect on why things occurred, see connections between human behaviors, make conclusions about causes, and more.

Outlines
00:00
👨👦 Introduction to Scatter Plots and Correlations between Variables

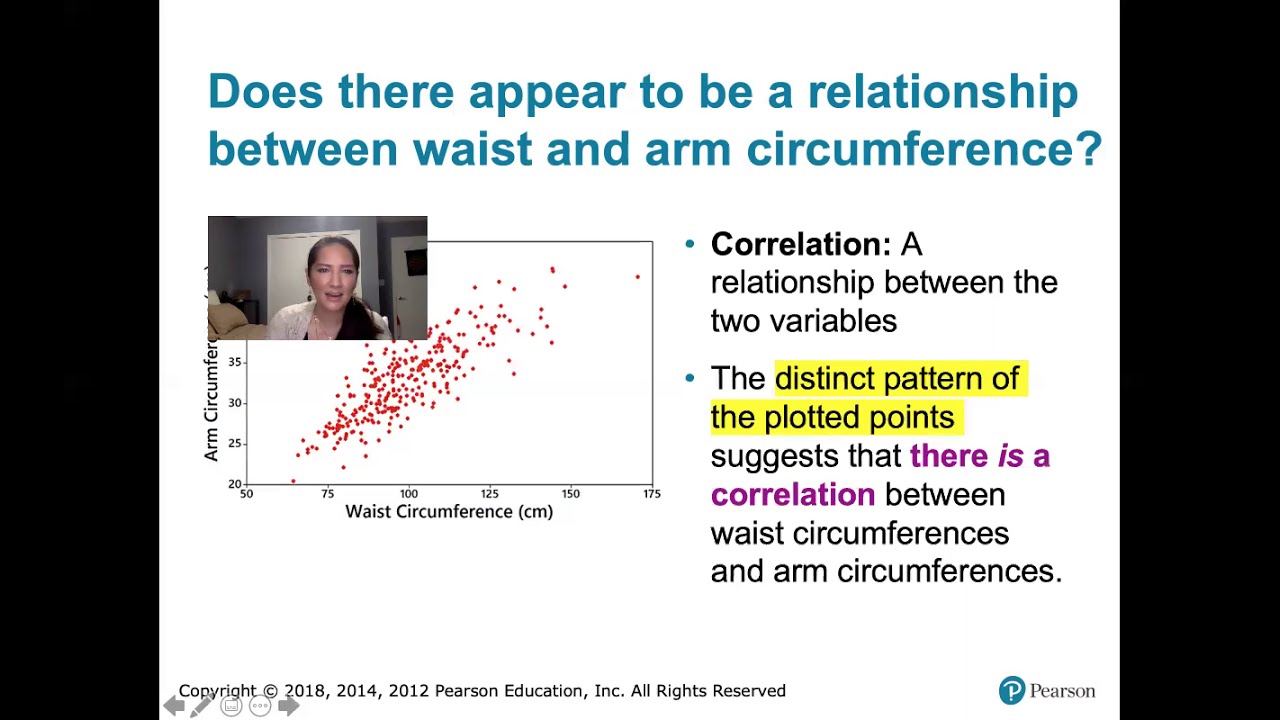
This paragraph introduces scatter plots as a useful way to visualize relationships between two continuous variables. It describes how to make a scatter plot and interpret the patterns and clusters. It then transitions to discussing linear relationships and correlations.

05:01
📈 Understanding Correlation Strength and Direction

This paragraph explains positive and negative correlation in more detail. It discusses how the strength of the correlation depends on how closely the two variables move together, and explains the correlation coefficient r, which measures the direction and strength of the linear relationship.

10:02
🤔 Correlation Does Not Imply Causation

This paragraph cautions that just because two variables are correlated does not mean that one causes the other. It gives examples of spurious correlations and explains how a third variable may actually be causing the observed correlation.

Mindmap
Keywords
💡Data Relationships
Data relationships refer to the connections or associations between different variables in a dataset. In the context of the video, it illustrates how one variable can be used to predict another. For example, the script explores whether the speed at which people drive is influenced by watching 'Fast & Furious' movies or if blink rates increase when people lie. These examples underscore the broader theme of investigating and understanding the dynamic interactions between various data points.
💡Scatter Plot
A scatter plot is a type of graph used to visualize the relationship between two continuous variables, showing how one variable is affected by another. The script praises scatter plots for their versatility and utility in statistical graphics, using the relationship between Old Faithful eruption durations and the time between eruptions as an example. This visualization helps identify patterns, trends, and clusters within the data, facilitating a deeper understanding of the underlying relationships.
💡Linear Relationships
Linear relationships describe a straight-line relationship between two variables, where changes in one variable predict changes in another in a consistent manner. The video uses the classic example of the heights of fathers and sons to illustrate this concept, showing how a taller father is likely to have a taller son. Karl Pearson's work on fitting a regression line to such data exemplifies how linear relationships can be quantified and used for prediction.
💡Regression Line
A regression line is a line that best fits the data points in a scatter plot, showing the general direction of the relationship between two variables. It's crucial for understanding and predicting how changes in one variable might affect another. The script mentions Karl Pearson's use of a regression line to describe the relationship between the heights of fathers and their sons, emphasizing its role in making accurate predictions.
💡Correlation
Correlation measures the strength and direction of a relationship between two variables. The video distinguishes between positive and negative correlations, using examples like exercise and heart health to illustrate how variables can move together in the same or opposite directions. Correlation is fundamental in assessing how closely two variables are linked, though it doesn't imply causation.
💡Correlation Coefficient (r)
The correlation coefficient, denoted as 'r,' quantifies the degree of correlation between two variables, ranging from -1 to 1. A value close to 1 or -1 indicates a strong positive or negative linear relationship, respectively, while a value near 0 suggests no linear relationship. The script uses this concept to explain the statistical measurement of relationships, emphasizing its importance in understanding the dynamics between variables.
💡R-Squared (R²)
R-squared is a statistical measure that represents the proportion of the variance for a dependent variable that's predictable from the independent variable(s). In the video, R-squared is explained as an indicator of how well the linear model explains the observed outcomes. For instance, if cigarette usage has an R² of 0.7 with lung health, it means 70% of the variance in lung health can be predicted by cigarette usage. This metric helps quantify the effectiveness of a model in predicting outcomes.
💡Causation
Causation implies that one event is the result of the occurrence of the other event; i.e., there is a cause-and-effect relationship between variables. The video emphasizes that correlation does not equal causation, illustrating this with examples like drownings and air conditioning usage or Nicolas Cage movies. This distinction is crucial in data analysis to avoid misinterpretation of statistical relationships as direct causes.
💡Spurious Correlations
Spurious correlations refer to apparent associations between two variables that are actually not related due to a coincidence or a third variable. The video illustrates this concept with humorous examples, such as the correlation between air conditioner sales and drownings, to highlight the importance of critical thinking and analysis when interpreting data relationships, emphasizing that not all observed correlations imply a direct or meaningful relationship.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion of a set of values. While not explicitly defined in the script, it underpins discussions on scaling correlation coefficients to account for different units of measurement. Understanding standard deviation is essential for interpreting correlation and regression analyses, as it helps quantify variability within the data, thereby informing the strength and significance of observed relationships.
Highlights

The speaker discusses how climate change is impacting agriculture, mentioning specific effects like changing rainfall patterns, rising temperatures, and drought.

There is a comparison of traditional farming practices versus modern precision agriculture and how technology like GPS, sensors, and data analytics can optimize crop yields.

The speaker highlights a few examples of farms using technology like self-driving tractors, drone imagery, and AI to become more efficient, sustainable, and productive.

Some key challenges facing the agricultural industry today include soil degradation, water scarcity, and the need for sustainability amidst population growth.

There is an analysis of how consumers are demanding more organic, local food, and how farms are adapting through renewable energy, waste reduction, and regenerative techniques.

The speaker emphasizes the importance of government policies, public-private partnerships, and farmer education to promote climate-smart agriculture.

A few innovative solutions mentioned include vertical indoor farms, hydroponics, aquaponics, and urban agriculture to produce more food using fewer resources.

There is a discussion of some promising technologies like GMOs, gene editing, and synthetic biology to develop crops with higher yields, better nutrition, and resilience to climate change.

The speaker stresses the need for more sustainable food systems, mentioning reducing food waste, shifting diets, and making agriculture carbon-neutral as crucial goals.

The conclusion focuses on agriculture adapting to climate change through technology, innovation, and a collaborative approach between farmers, governments, and consumers.

There is emphasis on agriculture playing a key role in both mitigating and adapting to climate change in the coming decades.

The speaker urges more funding and support for research and technology to build resilience and transform farming for a hotter, drier future.

Some interesting statistics are shared on the carbon footprint and water usage of different foods and how dietary choices impact sustainability.

There is a powerful call to action for policymakers, investors, and consumers to address climate change through agriculture reform and innovation.

The talk ends on an uplifting note about agriculture's critical role in feeding a growing population sustainably amidst climate change through shared ingenuity and purpose.

Transcripts

Browse More Related Video

10.1.1 Correlation - Linear, Nonlinear, Positive Linear, and Negative Linear Correlation Defined

Elementary Statistics - Chapter 10 Correlation and Regression

10.1.4 Correlation - Three Common Errors Involving Correlation

Introduction to Correlation & Regression, Part 1

Scatter Plots and Bivariate Data

Math 119 Chapter 10 Part 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating: