8.1.6 Basics of Hypothesis Testing - Power of a Hypothesis Test

Sasha Townsend - Tulsa
9 Nov 202010:01
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explores the concept of hypothesis testing power, defined as the probability of correctly rejecting a false null hypothesis. It discusses factors influencing power, such as significance level (alpha), population parameter values, and effect size. The script uses an example involving the 'X sort' method to illustrate how power varies with different population proportions, emphasizing the importance of a high power (commonly 80% or above) for an effective test and its role in determining the minimum required sample size.

Takeaways
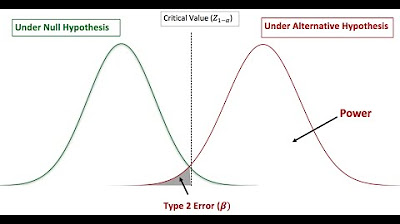
  • πŸ” The power of a hypothesis test is defined as the probability of rejecting a false null hypothesis, represented as one minus beta.
  • πŸ“ˆ Power is calculated using a specific significance level (alpha) and a value for the population parameter that serves as an alternative to the null hypothesis.
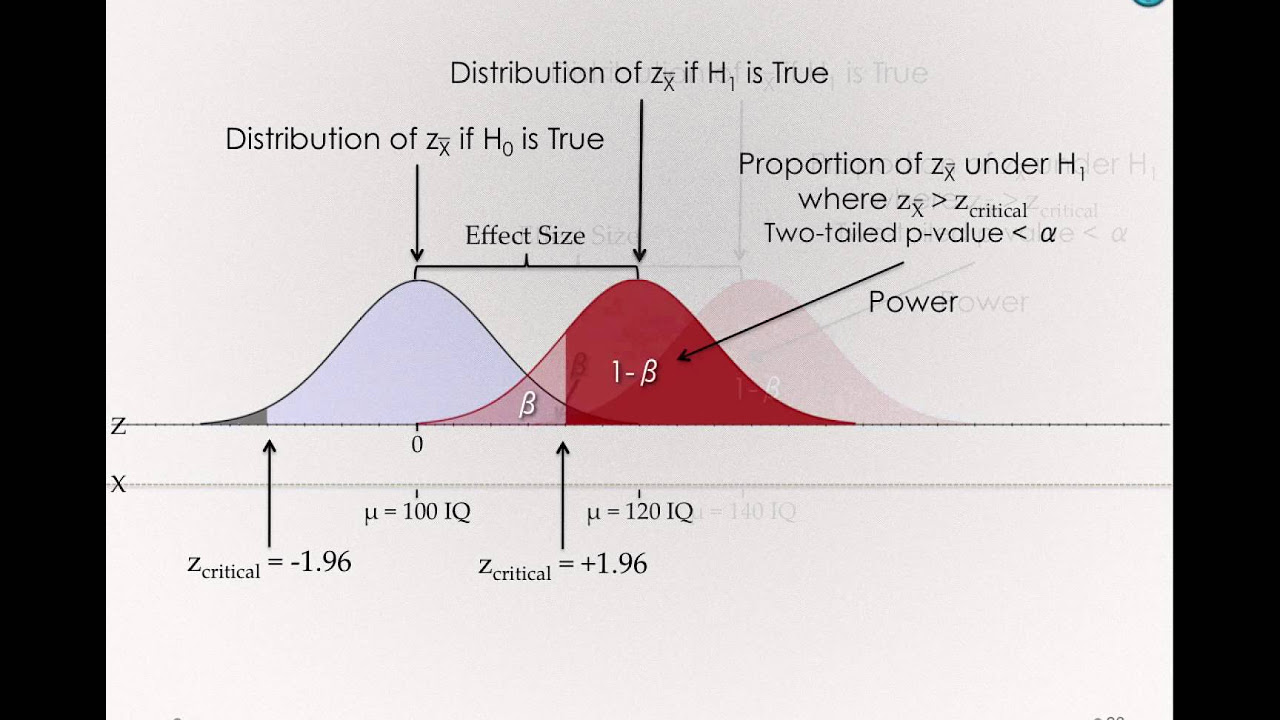
  • πŸ“Š Effect size, which is related to variance, is a crucial factor in determining the power of a hypothesis test, along with sample size.
  • πŸ”’ A lower alpha (probability of a type 1 error) results in a higher beta (probability of a type 2 error), thus affecting the power of the test.
  • πŸ”— The power of a hypothesis test requires a comparison value for the population parameter to assess its effectiveness.
  • πŸ“ The script emphasizes the importance of interpreting the power of a hypothesis test rather than just computing it.
  • 🌐 Reference to a website, realstatistics.com, is provided for further learning about power in hypothesis testing.
  • πŸ‘Ά An example involving the 'X sort' method and the birth of girls is used to illustrate the concept of hypothesis testing and power.
  • πŸ“‰ The power of a test increases as the difference between the true population proportion and the null hypothesis's claimed proportion increases.
  • 🎯 A common requirement for a hypothesis test's effectiveness is a power of at least 80%, which can guide the design of experiments and determine the minimum required sample size.
  • πŸ’‘ Understanding the concept of power and its interpretation is crucial for the course, without the need to delve into complex computations.
Q & A

  • What is the power of a hypothesis test?

    -The power of a hypothesis test is the probability (1 - Ξ²) of rejecting a false null hypothesis, which means correctly identifying when the null hypothesis is not true.

  • How is the power of a hypothesis test calculated?

    -The power is calculated using a specific significance level (alpha) and a particular value of the population parameter that serves as an alternative to the value assumed in the null hypothesis.

  • What is the significance of the significance level (alpha) in hypothesis testing?

    -The significance level (alpha) is the probability of a type 1 error, which is the error of rejecting a true null hypothesis. A lower alpha results in a higher probability of a type 2 error (beta).

  • What is the relationship between alpha and beta in hypothesis testing?

    -Alpha and beta are inversely related. A lower alpha increases the probability of a type 2 error (beta), and vice versa. The power of the test is 1 - beta.

  • What is effect size in the context of hypothesis testing?

    -Effect size is a measure of the magnitude of the difference between two groups or the strength of a relationship in statistical analysis, and it is related to variance. It affects the power of a hypothesis test.

  • Why is it important to consider the power of a hypothesis test when designing an experiment?

    -Considering the power of a hypothesis test helps determine the minimum required sample size to detect an effect if it exists, ensuring the experiment is capable of correctly rejecting a false null hypothesis with a reasonable probability.

  • What is a common threshold for the power of a hypothesis test?

    -A common requirement for the power of a hypothesis test is at least 80%, indicating a good chance of correctly rejecting a false null hypothesis when there is an effect.

  • How does the difference between the true population proportion and the null hypothesis proportion affect the power of a test?

    -As the difference between the true population proportion and the null hypothesis proportion increases, the power of the test also increases, making it more likely to correctly reject the null hypothesis.

  • What is the role of the alternative hypothesis in calculating the power of a test?

    -The alternative hypothesis provides a comparison value for the population parameter against the value assumed in the null hypothesis, which is necessary for computing the power of a hypothesis test.

  • Can you provide an example from the script where the power of a test is calculated?

    -In the script, an example is given where the null hypothesis states that the population proportion (p) is 0.5, and the alternative hypothesis tests different values of p (0.6, 0.7, 0.8, 0.9) to calculate the power of the test for each scenario.

  • What is the purpose of using a program like Minitab in the context of hypothesis testing?

    -Minitab is used to perform exact calculations for hypothesis testing, which can provide more accurate results than normal distribution approximations, especially for small sample sizes or when the test conditions are not met.

Outlines
00:00
πŸ” Understanding Hypothesis Test Power

The first paragraph introduces the concept of the power of a hypothesis test, which is the probability of correctly rejecting a false null hypothesis. It explains that power is calculated using a significance level (alpha) and a specific population parameter value that serves as an alternative to the null hypothesis. The paragraph also discusses how the power is affected by variables such as sample size, effect size, and alpha, and emphasizes the importance of interpreting power values. An example involving the 'x sort method' for having a girl is provided to illustrate the concept, with a focus on the qualitative understanding rather than computation.

05:03
πŸ“Š Interpreting Power in Hypothesis Testing

The second paragraph delves deeper into interpreting the power of a hypothesis test, using the same example of the 'x sort method'. It explains how the power increases as the difference between the true population proportion and the null hypothesis's claimed proportion grows. The paragraph also touches on the common requirement for a hypothesis test to have a power of at least 80% to be considered effective and how this can influence the design of an experiment, including determining the minimum required sample size. The summary concludes by reiterating the importance of understanding and interpreting power in hypothesis testing.

Mindmap
Keywords
πŸ’‘Hypothesis Test
A hypothesis test is a statistical method used to make decisions about a population parameter based on sample data. In the video, the focus is on the power of a hypothesis test, which is the probability of correctly rejecting a false null hypothesis. The script discusses how the power of a test is calculated and interpreted, emphasizing its importance in statistical analysis.
πŸ’‘Power
In the context of hypothesis testing, power refers to the probability of rejecting a false null hypothesis (1 - Ξ²). The video script explains that power is used to assess the effectiveness of a test and is influenced by factors such as sample size, effect size, and the significance level (alpha). The higher the power, the more likely the test is to detect an effect if it truly exists.
πŸ’‘Null Hypothesis
The null hypothesis is a statement of no effect or no difference that is tested in a statistical hypothesis test. In the video, the null hypothesis states that the population parameter is equal to a certain value (e.g., 0.5 for the probability of having a girl). The script uses the null hypothesis as a basis for discussing the power of a test and the probability of making a type II error.
πŸ’‘Alternative Hypothesis
The alternative hypothesis is a statement that contradicts the null hypothesis and represents the research hypothesis being tested. In the script, the alternative hypothesis is that the probability of having a girl is greater than 0.5, which is used to compare against the null hypothesis and calculate the test's power.
πŸ’‘Significance Level (Alpha)
The significance level, denoted by alpha, is the probability of making a type I error, which is the error of rejecting a true null hypothesis. The script mentions alpha as a key factor in calculating the power of a hypothesis test, with a common choice being 0.05, indicating a 5% risk of a type I error.
πŸ’‘Type I Error
A type I error occurs when the null hypothesis is incorrectly rejected when it is actually true. The script explains that the significance level (alpha) is directly related to the probability of a type I error, and a lower alpha results in a higher probability of a type II error (beta).
πŸ’‘Type II Error (Beta)
A type II error happens when the null hypothesis is not rejected when it is actually false. The script discusses beta as the probability of a type II error and explains that power is the complement of beta (1 - Ξ²), indicating the probability of correctly rejecting a false null hypothesis.
πŸ’‘Effect Size
Effect size is a measure of the magnitude of the difference between two groups or the strength of a relationship in statistical analysis. The script mentions effect size in relation to variance and its impact on the power of a hypothesis test, with a larger effect size generally leading to greater power.
πŸ’‘Sample Size
Sample size refers to the number of observations or elements included in a sample used for statistical analysis. The video script discusses how the sample size affects the power of a hypothesis test, with larger sample sizes typically increasing the power to detect an effect.
πŸ’‘Interpreting Power
Interpreting power involves understanding the likelihood of correctly rejecting a false null hypothesis. The script provides an example of interpreting power values in a table, explaining how a test with a power of 0.18 (18%) has a low chance of correctly rejecting the null hypothesis when the true population proportion is slightly different from the null hypothesis value.
πŸ’‘Minimum Required Sample Size
The minimum required sample size is the smallest number of observations needed to achieve a desired level of power for a hypothesis test. The script suggests that a power of at least 80% is often considered adequate, and this can be used to determine the necessary sample size to ensure the test is effective.
Highlights

The power of a hypothesis test is defined as the probability of rejecting a false null hypothesis.

Power is calculated using a specific significance level (alpha) and an alternative population parameter value.

The power of a hypothesis test requires a comparison value for the population parameter.

Effect size, related to variance, influences the power of a hypothesis test.

A lower alpha increases the probability of a type 2 error (beta), thus reducing the power.

The video discusses interpreting the power of a hypothesis test without direct computation.

An example is given using the X sort method and the probability of having a girl.

Null and alternative hypotheses are set up for testing the effectiveness of the X sort method.

Power increases as the difference between the true and claimed population proportions increases.

A common requirement for a hypothesis test is a power of at least 80%.

The significance level alpha is associated with the probability of a type 1 error.

The power of a test can be used to determine the minimum required sample size for an experiment.

The video emphasizes the importance of understanding power and its interpretation in hypothesis testing.

The relationship between power and the choices of population parameter values is discussed.

As the true population proportion deviates more from the null hypothesis value, the power of the test increases.

The video provides an example of calculating power using Minitab for different population proportions.

The concept of type 2 error (beta) is explained as the complement of the test's power.

The importance of the effect size in determining the power of a hypothesis test is highlighted.

Transcripts

Browse More Related Video

Introduction to power in significance tests | AP Statistics | Khan Academy

Power and Sample Size Calculation

Factors Affecting Power - Effect size, Variability, Sample Size (Module 1 8 7)

AP Statistics Unit 6 Summary Review Inference for Proportions Part 2 Significance Tests

5 4 Power Calculations for difference of two means

Power Analysis, Clearly Explained!!!

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Hypothesis TestingStatistical PowerType 1 ErrorType 2 ErrorSignificance LevelPopulation ParameterSample SizeEffect SizeMinitab SoftwareStatistical Decisions