Elementary Stats Lesson #15

The instructor begins by expressing excitement about reaching a significant point in the course: the study of inferential statistics. After covering the first eight chapters, the focus shifts to generalizing information from a sample to a larger population. Two main areas of inferential statistics are introduced: estimation of population parameters and hypothesis testing. The lesson specifically starts with parameter estimation, which involves using sample statistics to make inferences about population parameters such as the mean, standard deviation, or proportion. The importance of understanding the behavior of sample statistics is emphasized, especially in the context of estimating population proportions and means.

The video script delves into the process of estimating the population proportion using a sample. A point estimate is first calculated, which in this case is the sample proportion, obtained by dividing the number of successes (e.g., individuals in favor of the death penalty) by the sample size. The script then explains the concept of a confidence interval, which provides a range of plausible values for the population proportion. The margin of error, calculated based on the sample proportion, confidence level, and sample size, is crucial for constructing this interval. The instructor illustrates this with an example from a Quinnipiac University poll, discussing how to calculate the point estimate and the margin of error to estimate the population proportion who favor the death penalty.

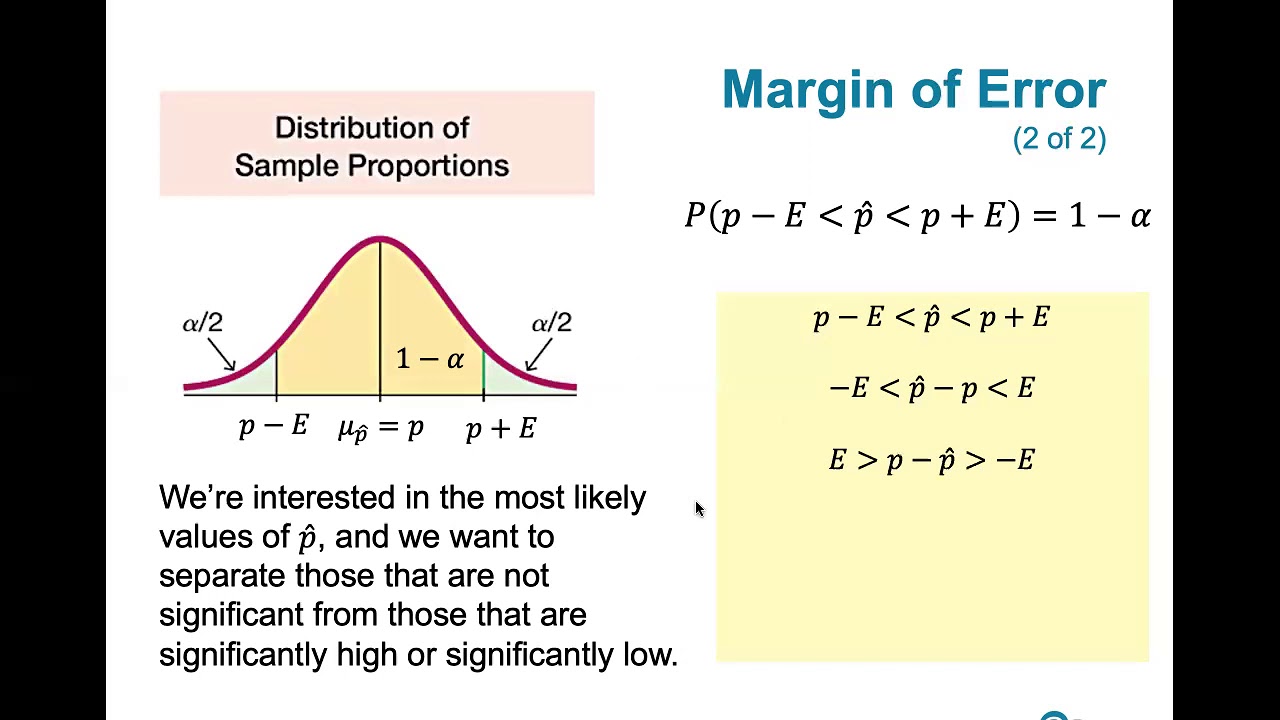
The script explains the factors influencing the margin of error in estimating a population proportion. The margin of error is determined by the confidence level, sample size, and the population's inherent variability. The higher the confidence level, the larger the margin of error to ensure a greater likelihood of capturing the true population parameter. Similarly, a larger sample size reduces the margin of error due to decreased standard error. The script also discusses how to calculate the margin of error for the Quinnipiac poll example, emphasizing the role of the sample proportion's standard error and the critical value from the standard normal distribution.

The script provides a step-by-step guide on calculating confidence intervals for a population proportion. It starts with computing the sample proportion and then uses this to estimate the standard error. The margin of error is determined by multiplying the standard error by a critical value from the standard normal distribution, which corresponds to the desired confidence level. The confidence interval is then constructed by adding and subtracting the margin of error from the point estimate. The script also explains the central limit theorem's role in justifying the use of a normal distribution for sample proportions and how to find critical values for different confidence levels.

The script revisits the central limit theorem, which states that the sampling distribution of the sample proportion is approximately normal with a mean equal to the population proportion. It explains how to use the standard normal table or a calculator to find the critical value for a given confidence level. The 1.96 value, which corresponds to a 95% confidence level, is derived from the theorem and is used to construct the confidence interval. The script emphasizes the importance of the sample size in meeting the normality condition and the independence of sampling.

The script presents a general formula for constructing confidence intervals for a population proportion, emphasizing the components involved: the point estimate, standard error estimate, and the critical value. It explains that the point estimate and standard error are derived from the sample, while the critical value is determined by the desired confidence level. The script also provides a 'cheater table' for common confidence levels and their corresponding critical values, including how to obtain these values using a calculator's inverse normal function.

The script discusses the use of technology, specifically calculators, to simplify the process of constructing confidence intervals. It provides a guide on using a TI-84 calculator to perform a one proportion z interval (one prop z int) calculation. The process involves entering the number of successes, sample size, and confidence level into the calculator, which then computes the confidence interval. The script illustrates this with examples, showing how the calculator can efficiently handle the arithmetic and lookup of critical values.

The script addresses the problem of determining the necessary sample size to achieve a specific margin of error when estimating a population proportion. It presents a formula for calculating the required sample size based on the desired margin of error, the confidence level, and an estimate of the population proportion. The script explains two methods for handling the absence of a prior estimate for the population proportion: using an estimate from a previous study or employing a conservative approach by assuming a proportion of 0.50, which maximizes the required sample size.

The instructor concludes the lesson by summarizing the importance of the confidence interval as a tool for estimating population proportions and the significance of the sample size in achieving a desired margin of error. The script hints at future lessons that will cover the estimation of population means and other aspects of statistical inference, encouraging students to look forward to becoming proficient in these areas.