7.1.6 Estimating a Pop. Proportion - The Right Sample Size for a Given Error and Confidence Level
TLDRThis video script offers a detailed explanation on calculating the necessary sample size for estimating a population proportion with a specific margin of error and confidence level. It introduces key variables, explains the use of the z-score for confidence, and demonstrates the formula manipulation to solve for sample size. The script also addresses scenarios with and without prior estimates, emphasizing the importance of rounding up the sample size to ensure accuracy. Practical examples, such as estimating the percentage of left-handed Californians, illustrate the process clearly.
Takeaways
- 📚 The video discusses the process of finding the necessary sample size to estimate a population proportion with a desired level of accuracy and confidence.
- 🔢 Key variables include the population proportion (p), sample proportion (p-hat), sample size (n), margin of error (e), and the critical z-value (z-sub-alpha/2).
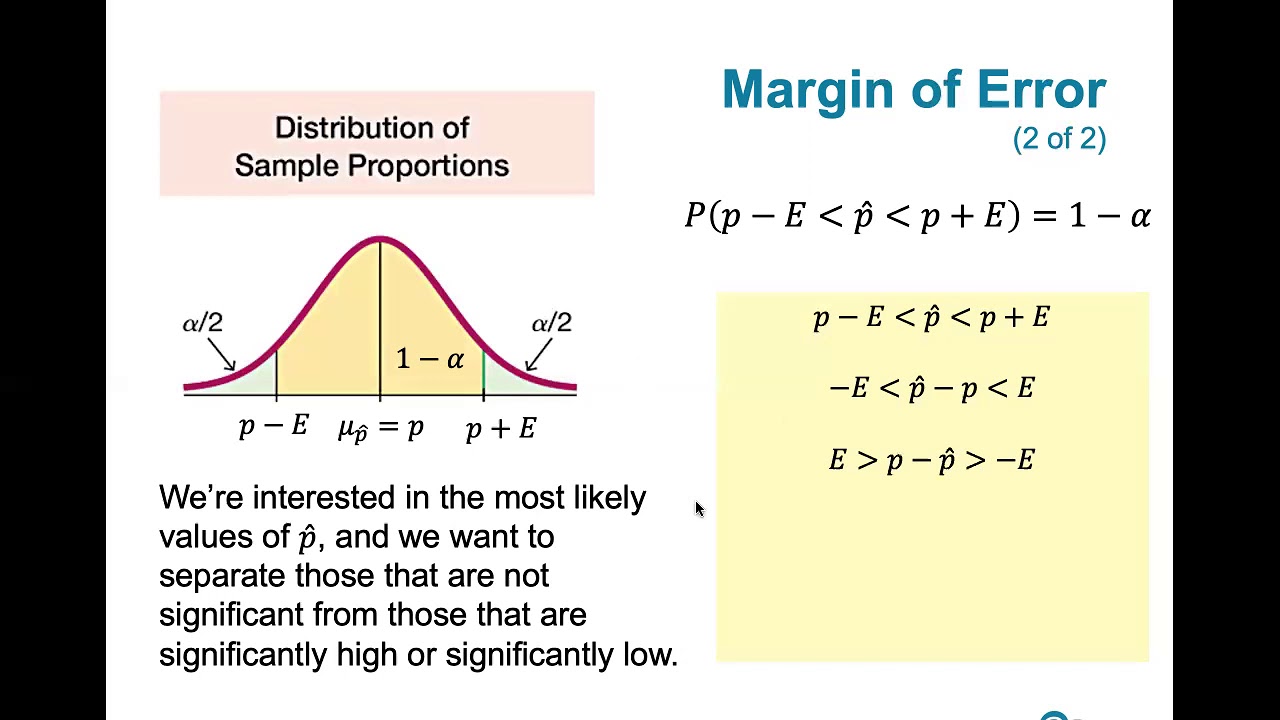
- 📉 The margin of error formula is derived from the standard deviation of the sampling distribution of the sample proportion.
- 🧐 If a prior estimate of the population proportion is known, it's used as p-hat; otherwise, p-hat and q-hat are assumed to be 0.5, representing no prior knowledge.
- 🔍 The appropriate z-score is determined by the desired confidence level, which corresponds to the area under the standard normal distribution.
- 📝 The formula for sample size is derived by manipulating the margin of error formula and solving for n.
- ➗ When calculating sample size, always round up to the nearest whole number to ensure the margin of error is not larger than desired.
- 📈 The larger the desired confidence level or the smaller the acceptable margin of error, the larger the required sample size.
- 🤔 The absence of prior information about the population proportion results in a larger sample size compared to when prior information is available.
- 📊 The video provides an example of estimating the percentage of left-handed California residents, illustrating the calculation with and without prior estimates.
- 🔑 The importance of minimizing error (e) is emphasized, as it directly impacts the accuracy of the population proportion estimate.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is how to find the sample size necessary to estimate a population proportion with a desired accuracy and confidence level.
What are the variables used in the notation for confidence intervals for population proportions?
-The variables used in the notation are p (population proportion), p-hat (sample proportion), n (sample size), e (margin of error), and z sub alpha over 2 (critical value corresponding to the confidence level).
What is the significance of z sub alpha over 2 in the context of the video?
-Z sub alpha over 2 is a z-score that separates an error area of alpha over 2 in the right tail from the rest of the area under the standard normal distribution, representing the confidence level.
How can the margin of error be calculated?
-The margin of error is calculated as the critical value z sub alpha over 2 multiplied by the square root of the standard deviation of the sampling distribution of the sample proportion.
What algebraic steps are taken to solve for the sample size n in the margin of error formula?
-The steps include dividing both sides by z sub alpha over 2, squaring both sides to eliminate the square root, cross-multiplying, and then dividing by e squared to isolate n.
What is the default value for p-hat and q-hat when there is no prior estimate available?
-When there is no prior estimate, p-hat and q-hat are both set to one-half (0.5), assuming equal probability of success and failure.
Why is it important to round up when calculating the sample size n?
-Rounding up ensures that the error is minimized, which is preferable as a larger error could lead to a less accurate estimate than desired.
What is the purpose of using a z-score in finding the sample size?
-The z-score corresponds to the desired confidence level and helps determine the critical value needed to calculate the margin of error and subsequently the sample size.
How does having a prior estimate of p-hat affect the required sample size?
-Having a prior estimate of p-hat can reduce the required sample size because it provides more accurate information about the population, allowing for a more precise estimation with fewer samples.
Can you provide an example of how the sample size is calculated in the video?
-In the example given, to estimate the percentage of left-handed California residents with a 99% confidence level and a maximum error of 3 percentage points, the formula is used with a z-score of 2.575 and an error of 0.03, resulting in a sample size of approximately 1842 when no prior estimate is available.
Outlines
📊 Estimating Population Proportion: Sample Size and Confidence
This paragraph introduces the concept of determining the necessary sample size to estimate a population proportion with a specified degree of accuracy and confidence level. Key variables such as population proportion (p), sample proportion (p-hat), sample size (n), margin of error (e), and the critical z-value (z-sub-alpha/2) are defined. The process involves using the margin of error equation, solving for n, and emphasizing the importance of rounding up to ensure the error doesn't exceed the desired level. The formula for sample size calculation is provided, and the scenario of lacking a prior estimate for p-hat is discussed, suggesting the use of 0.5 for both p-hat and q-hat (1 - p-hat) as a conservative approach.
🔍 Calculating Sample Size for a Confidence Interval: An Example with Left-Handed Individuals
The second paragraph presents a practical example to calculate the sample size needed to estimate the percentage of left-handed California residents with a 99% confidence level and a margin of error of 3 percentage points. It begins by assuming no prior estimate of the proportion of left-handed individuals, using p-hat and q-hat values of 0.5. The z-score for a 99% confidence level is identified as 2.575. By substituting the values into the sample size formula, the calculated sample size is approximately 1842, which is rounded up to ensure the margin of error is not exceeded. The importance of rounding up is reiterated to maintain the desired level of accuracy.
📈 Impact of Prior Information on Sample Size Determination
The final paragraph discusses the impact of prior information on determining the sample size, using the same example of estimating the percentage of left-handed California residents but this time with prior studies suggesting that 10% are left-handed. With this information, p-hat is adjusted to 0.10, and the calculation is redone, resulting in a significantly smaller required sample size of 664. This illustrates the advantage of having prior information, which can substantially reduce the number of individuals needed for the survey, thus making the sampling process more efficient.
Mindmap
Keywords
💡Sample Size
💡Population Proportion
💡Sample Proportion
💡Margin of Error
💡Confidence Level
💡Critical Value
💡Standard Normal Distribution
💡Algebraic Manipulation
💡Rounding Up
💡Left-Handed Residents
Highlights
Lesson 7.1 discusses the calculation of sample size required to estimate a population proportion with a specific degree of accuracy and confidence.
Variables p, p-hat, n, e, and z-sub-alpha/2 are defined for use in confidence intervals for population proportions.
The margin of error formula is derived from the standard deviation of the sampling distribution of the sample proportion.
Solving the margin of error equation for sample size n involves algebraic manipulation.
When no prior estimate of p-hat is available, p-hat and q-hat are assumed to be 0.5.
The necessity to round up the calculated sample size n to ensure the desired margin of error is emphasized.
An example involving estimating the percentage of left-handed California residents is presented.
For the left-handed example, a 99% confidence level and a maximum error of 3 percentage points are specified.
The z-score corresponding to a 99% confidence level is identified as 2.575.
Calculating sample size with no prior estimate results in a need for 1842 California residents to be surveyed.
The impact of prior studies on reducing the required sample size is demonstrated in part B of the example.
With a prior estimate suggesting 10% left-handedness, the sample size required is significantly reduced to 664.
The importance of using prior information to decrease the sample size and increase survey efficiency is highlighted.
The process of substituting values into the sample size formula is explained step by step.
The significance of the margin of error in determining the accuracy of the population proportion estimate is discussed.
The transcript concludes by reiterating the importance of rounding up the sample size to ensure accuracy.
Transcripts
Browse More Related Video

7.2.4 Estimating a Population Mean - Sample Size for a Desired Margin of Error and Confidence Level

Elementary Stats Lesson #15

Math 119 Chap 7 part 1

Statistics 101: Confidence Intervals, Estimating Sample Size Needed
7.1.4 Estimating a Population Proportion - Margin of Error and Computing Confidence Intervals

Elementary Stats Lesson #16
5.0 / 5 (0 votes)
Thanks for rating: