Calculus AB Homework 4.4: Relative Extrema
TLDRThis educational video script guides viewers through the application of the first and second derivative tests to identify local extrema in various mathematical functions. The first part demonstrates the first derivative test by finding critical points and analyzing sign changes to determine relative maxima and minima. The second part employs the second derivative test, evaluating the concavity of functions to ascertain relative extrema quickly. The script covers multiple examples, including polynomial and exponential functions, offering a comprehensive understanding of extremum problems.
Takeaways
- 📚 The video covers the use of the first and second derivative tests for finding local extrema in calculus problems.
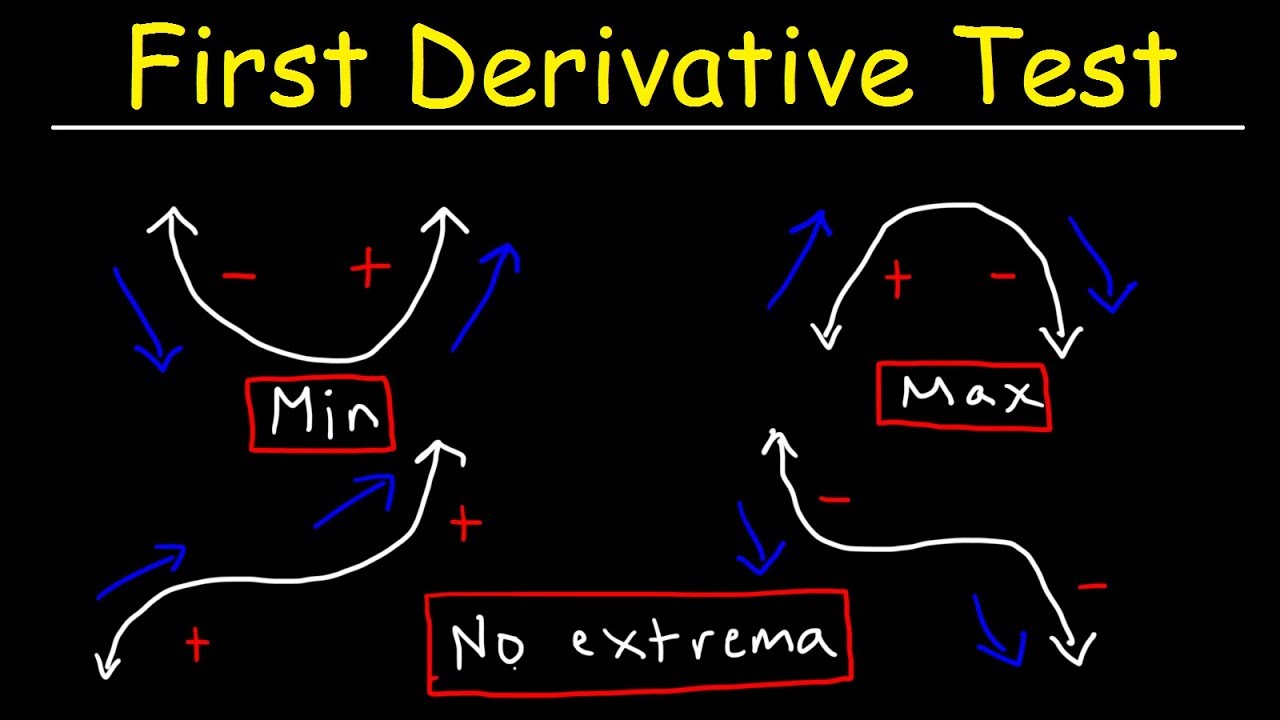
- 🔍 The first derivative test involves finding critical values where the derivative is zero or undefined and analyzing the sign changes of the derivative around these points.
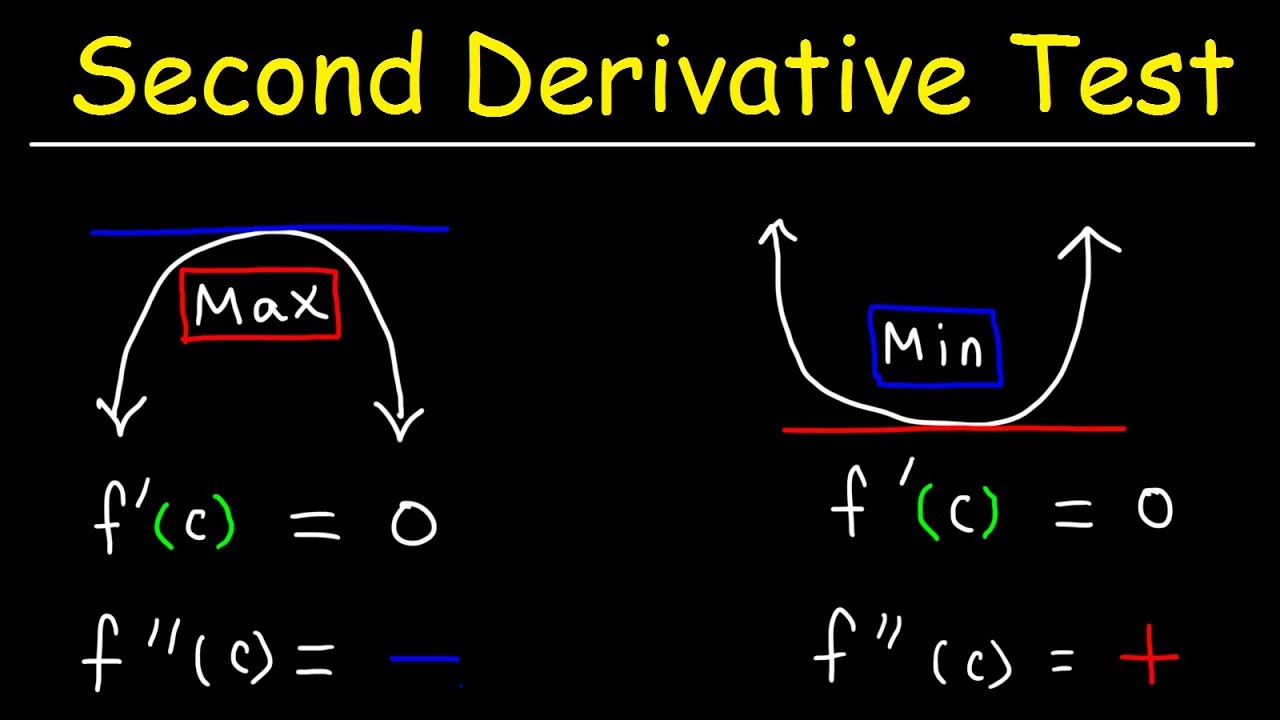
- 📈 The second derivative test is used to determine the concavity of a function by evaluating the sign of the second derivative at critical points to find local maxima and minima.
- 📝 The script demonstrates how to apply these tests to several functions, including polynomial and exponential functions, with step-by-step calculations.
- 📉 The process of finding critical values includes setting the first derivative equal to zero and solving for x, while considering the domain of the function.
- 📌 For the first derivative test, test points are chosen to determine the sign of the derivative in intervals around critical values.
- 📐 The second derivative test requires finding the second derivative of the function and evaluating it at the critical points to determine concavity.
- 📊 The video explains that a negative second derivative indicates a concave down graph at that point, suggesting a local maximum, while a positive second derivative indicates a concave up graph, suggesting a local minimum.
- 🤔 The importance of considering the domain of the original function is emphasized, as the derivative test results must be applicable within the domain.
- ⚠️ The script clarifies that the first derivative test alone may not suffice for piecewise functions, where the behavior of the function changes at certain points.
- 📚 The video concludes with a series of examples applying these concepts, highlighting the process of identifying critical points, evaluating derivatives, and concluding the nature of extrema.
Q & A
What is the first derivative test used for in the context of this video?
-The first derivative test is used to determine the local extreme values, or relative maxima and minima, of a function by finding critical values where the derivative is zero or undefined.
How does the video approach the first problem involving the function y = x^2 - x - 1?
-The video finds the derivative of the function, sets it equal to zero to find the critical value, and then uses a sign chart to determine the nature of the extreme value at x = 1/2, concluding there is a relative minimum.
What is the second derivative test for extrema, and when is it used in the video?
-The second derivative test is used to determine the concavity of a function at its critical points. The video uses it after finding critical values to quickly identify whether they correspond to relative maxima, minima, or points of inflection without needing to perform a sign chart.
In the function y = -2x^3 + 6x^2 - 3, how does the video find the critical values?
-The video finds the first derivative, sets it equal to zero, factors out common terms, and solves for x to get the critical values at x = 0 and x = 2.
What is the significance of the second derivative being positive or negative in the second derivative test?
-A positive second derivative indicates that the function is concave up, suggesting a relative minimum, while a negative second derivative indicates that the function is concave down, suggesting a relative maximum.
How does the video handle the piecewise function y = 3 - x^2 for x < 0 and y = x^2 + 1 for x ≥ 0?
-The video finds the derivative for each piece and sets it equal to zero to find critical values. It then checks the differentiability at the domain split (x = 0) and uses test points to determine the behavior of the function around the critical value.
What is the role of the first derivative in the second derivative test?
-The first derivative is used to find the critical values where it equals zero or is undefined. These values are then used in the second derivative test to determine the nature of the extrema.
In the video, what is the condition for a critical point to be considered an extremum using the second derivative test?
-A critical point is considered an extremum if the second derivative at that point is non-zero, with a positive value indicating a relative minimum and a negative value indicating a relative maximum.
How does the video script handle the function y = x * e^(1/x) when finding critical values?
-The video uses the product rule to find the first derivative, sets it equal to zero, and solves for x to find the critical value, ensuring that e^(1/x) is never zero.
What is the conclusion for the function y = x * e^(-x) regarding its relative extrema?
-The video concludes that there is a relative maximum at x = 1, as the first derivative is zero and the second derivative is negative, indicating the function is concave down at that point.
Outlines
📚 First Derivative Test for Local Extrema
The paragraph introduces the first derivative test for finding local extrema in calculus. It explains the process of identifying critical values where the derivative of a function is zero or undefined. The example function y = x^2 - x - 1 is used to demonstrate the test, showing how to find the derivative, set it to zero to solve for x, and determine the nature of the critical point by checking the sign change of the derivative around the critical value x = 1/2. The conclusion is that y has a relative minimum at x = 1/2.
📐 Second Derivative Test Application
This section delves into the second derivative test for extrema, starting with the function y = -2x^3 + 6x^2 - 3. The critical values are calculated by setting the first derivative to zero, resulting in x = 0 and x = 2. A thorough explanation of the first derivative test is provided, including choosing test points and analyzing the sign changes of the derivative to determine the nature of the extrema. The conclusion identifies a relative minimum at x = 0 and a relative maximum at x = 2.
🔍 Detailed Analysis of Multiple Extrema
The paragraph discusses the process of finding multiple points of extrema for the function y = 2x^4 - 4x^2 + 1. The first derivative is calculated, and critical values are determined by setting the derivative equal to zero, resulting in x = -1, 0, and 1. The behavior of the derivative around these points is analyzed using test points, leading to the identification of a relative minimum at x = -1, a relative maximum at x = 0, and another relative minimum at x = 1.
🌐 Product and Chain Rule in Derivatives
This section presents a function y = x * e^(1/x) and explains the process of finding its derivative using the product and chain rules. The critical value is identified by setting the derivative equal to zero, resulting in x = 1. The behavior of the original function around the critical value is analyzed, noting that the function is increasing until x = 0 and then decreasing, with a relative minimum at x = 1.
📉 Derivative Analysis of a Piecewise Function
The paragraph examines a piecewise function y = 3 - x^2 for x < 0 and y = x^2 + 1 for x ≥ 0. The derivative of the function is calculated, and the critical value at x = 0 is analyzed for differentiability. The function is found to be differentiable at x = 0, with the derivative being zero at this point. However, the function does not have a relative maximum or minimum, as the derivative does not exhibit a sign change.
📈 Second Derivative Test for Concavity
The paragraph demonstrates the use of the second derivative test for extrema using the function y = 3x - x^3 + 5. The first derivative is calculated, and critical values are found by setting it to zero, resulting in x = ±1. The second derivative is then calculated, and its values at the critical points are used to determine the concavity of the function at those points, identifying a relative maximum at x = 1 and a relative minimum at x = -1.
🤔 Second Derivative Test for Multiple Critical Points
The function y = x^5 - 80x + 100 is analyzed for extrema using the second derivative test. The first derivative is calculated, and critical values are determined by setting it to zero, resulting in x = ±2. The second derivative is then evaluated at these points, leading to the identification of a relative maximum at x = -2 and a relative minimum at x = 2.
📊 Second Derivative Test with Quadratic Factors
The paragraph discusses the second derivative test for the function y = x^3 + 3x^2 - 2, which has critical values at x = 0 and x = -2. The second derivative is calculated, and its values at the critical points indicate concavity, leading to the conclusion that there is a relative minimum at x = 0 and a relative maximum at x = -2.
🧩 Second Derivative Test for Polynomial Functions
The function y = 3x^5 - 25x^3 + 60x + 20 is analyzed using the second derivative test. The first derivative is calculated, and four critical values are found. The second derivative is then evaluated at these points, resulting in two relative maxima at x = ±2 and two relative minima at x = ±1.
🌟 Second Derivative Test for Exponential Functions
The paragraph examines the function y = x * e^x and identifies a critical value at x = -1 using the first derivative. The second derivative test is applied, and the positive second derivative at the critical point indicates a concave up graph, confirming a relative minimum at x = -1.
📚 Second Derivative Test for a Complex Function
The function y = x * e^(-x) is analyzed for extrema using the second derivative test. The first derivative is calculated, and the critical value at x = 1 is determined. The second derivative is then evaluated, and its negative value at x = 1 indicates a concave down graph, confirming a relative maximum at this point.
Mindmap
Keywords
💡Derivative
💡Critical Values
💡First Derivative Test
💡Second Derivative Test
💡Extrema
💡Relative Maximum/Minimum
💡Product Rule
💡Chain Rule
💡Concave Up/Down
💡Sign Change
💡Differentiable
Highlights
Introduction to using the first and second derivative tests for extrema in calculus.
Explanation of the first derivative test to find relative maximum and minimum values of a function.
Critical values are identified as points where the derivative is zero or undefined.
Derivative of the function y = x^2 - x - 1 is found to be 2x - 1.
Critical value x = 1/2 found for the function y = x^2 - x - 1, indicating a potential relative extremum.
Use of test points to determine the sign of the derivative and function's increasing or decreasing nature.
Visual method of drawing a number line to analyze the behavior of the derivative.
Application of the first derivative test to the function y = -2x^3 + 6x^2 - 3.
Identification of two critical values, x = 0 and x = 2, for the function y = -2x^3 + 6x^2 - 3.
Second derivative test introduced as an alternative method for finding extrema.
Second derivative test applied to y = 3x - x^3 + 5, revealing a relative maximum at x = 1 and a minimum at x = -1.
Demonstration of the product rule and chain rule in finding derivatives of more complex functions.
Piecewise function analysis with different expressions for different domains.
Differentiability check at the boundary of piecewise functions to ensure the existence of the derivative.
Application of the second derivative test to functions with multiple critical values, such as y = x^5 - 25x^3 + 60x + 20.
Conclusion of relative extrema based on the concavity of the graph determined by the second derivative.
Final problem analysis with function y = xe^(-x), using both the first and second derivative tests to find a relative maximum at x = 1.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: