Finding Relative Extrema
TLDRThe video script introduces the concept of relative extrema, which includes relative minima and maxima, also known as local minima and maxima. These points represent the lowest and highest values within a small interval on a graph, respectively. The video explains that relative extrema occur at critical values, which are found where the first derivative of a function is either zero or undefined. The script provides examples of how to find these critical points by calculating the first derivative of given functions and setting it equal to zero or identifying where it's undefined. It also hints that future lessons will cover how to determine whether a critical point is a hilltop (relative maximum) or a valley bottom (relative minimum), adding to the intrigue and educational value of the content.
Takeaways
- 📌 The term 'extrema' refers to either a relative minimum or a relative maximum, also known as local minima or maxima.
- 📌 A relative minimum is the lowest point within a small interval on a graph, like the bottom of a valley.
- 📌 A relative maximum is the highest point within a small interval on a graph, analogous to the top of a hill.
- 📌 Relative extrema occur at critical values, which are points where the first derivative is either zero or undefined.
- 📌 To find relative extrema, calculate the first derivative of the function and solve for where it equals zero or is undefined.
- 📌 The first derivative of a function can be found using basic differentiation rules, such as the power rule.
- 📌 When the first derivative is undefined, it indicates a potential relative extremum, but the nature (minimum or maximum) is determined later.
- 📌 The process of determining whether a critical point is a relative maximum or minimum will be covered in a future lesson.
- 📌 The script provides examples of finding the first derivative and critical points for different functions.
- 📌 It's important to note that the presence of a lower or higher point outside the interval does not affect the classification of a relative extremum.
- 📌 The concept of relative extrema is foundational for understanding local behavior of functions in calculus.
- 📌 Future lessons will delve into methods for classifying critical points as either relative maxima or minima.
Q & A
What is the term 'extrema' referring to in the context of the video?
-In the context of the video, 'extrema' refers to either a relative maximum or a relative minimum, also known as local maxima or local minima.
What is the definition of a relative minimum on a graph?
-A relative minimum is the lowest point within a small interval on a graph, often described as the bottom of a valley.
How is a relative maximum different from the highest point on the entire graph?
-A relative maximum is the highest point within a small interval on the graph, but it is not necessarily the highest point on the entire graph.
What are the two ways in which critical values are defined?
-Critical values are defined as either where the first derivative equals zero or where the first derivative is undefined.
What is the first step in finding relative extrema?
-The first step in finding relative extrema is to find the critical values by setting the first derivative equal to zero or finding where it is undefined.
What does the video suggest to determine if a critical point is a hilltop or a valley bottom?
-The video suggests that this determination will be covered in a future lesson, implying that additional methods or tests are needed beyond finding critical values.
What is the first derivative of the function f(x) = 8x - 8?
-The first derivative of the function f(x) = 8x - 8 is f'(x) = 8x - 8.
At what value of x does the first derivative of f(x) = 8x - 8 equal zero?
-The first derivative of f(x) = 8x - 8 equals zero when x equals one.
What does it mean if the first derivative of a function is undefined at a certain point?
-If the first derivative of a function is undefined at a certain point, it indicates a potential relative extrema or a point of abrupt change in the function's slope, such as a sharp corner or cusp.
What is the first derivative of the function f(x) = 5(x - 3)^(1/2)?
-The first derivative of the function f(x) = 5(x - 3)^(1/2) is f'(x) = (5/2) * (x - 3)^(-1/2).
At what value of x does the first derivative of f(x) = 20x^(1/2) - x^2 become undefined?
-The first derivative of f(x) = 20x^(1/2) - x^2 becomes undefined at x equals zero due to division by zero in the derivative expression.
What is the value of x for which the first derivative of f(x) = 20x^(1/2) - x^2 equals zero?
-The first derivative of f(x) = 20x^(1/2) - x^2 equals zero when x equals the cube root of 25, which is 5^(2/3) or approximately 2.714.
Outlines
📈 Introduction to Relative Extrema
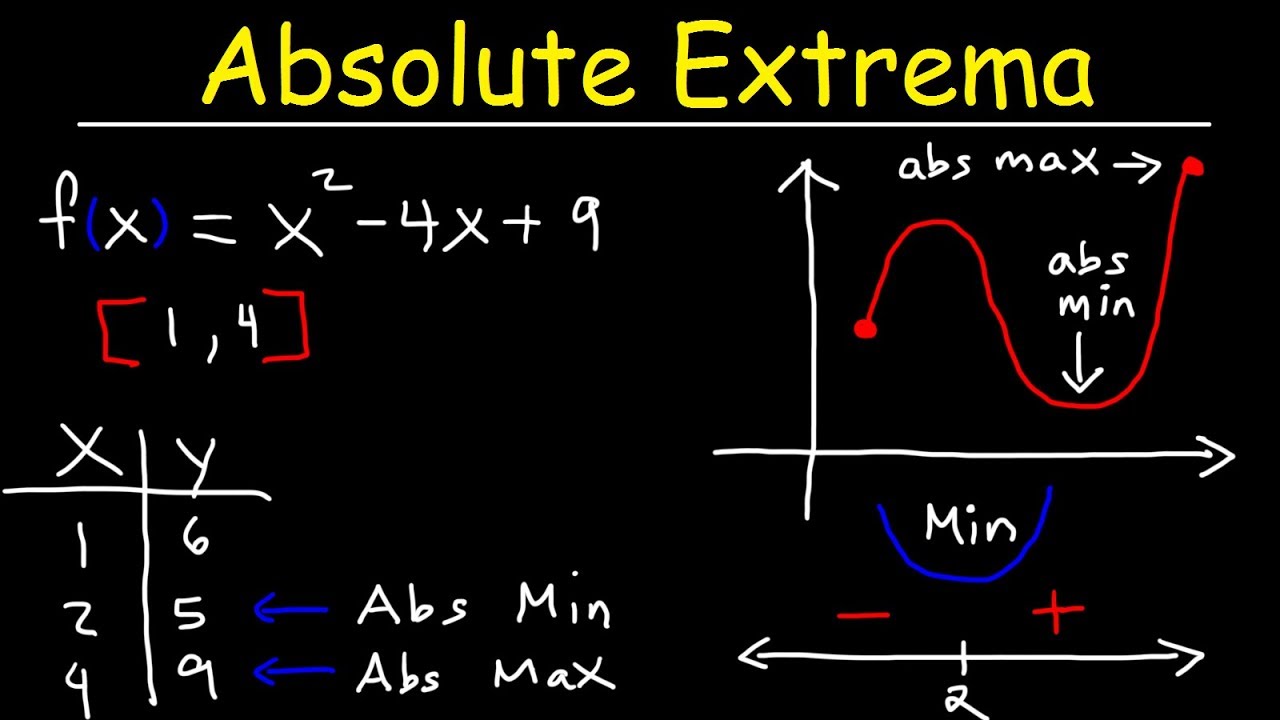
This paragraph introduces the concept of relative extrema, which includes relative minima and maxima, also known as local minima and maxima. It explains that a relative minimum is the lowest point within a small interval on a graph, like the bottom of a valley, while a relative maximum is the highest point, akin to the top of a hill. The speaker illustrates these concepts using a graph and emphasizes that these points are local, not necessarily the absolute highest or lowest on the entire graph. The paragraph also mentions that relative extrema occur at critical values, which are found by setting the first derivative of the function equal to zero or where it is undefined. An example is given where the first derivative is calculated as eight x minus eight, leading to a relative extrema at x equals one.
🔍 Identifying Critical Points for Extrema
The second paragraph delves into the process of identifying critical points associated with relative extrema. It explains that critical values can be found where the first derivative of a function is either zero or undefined. The paragraph provides two examples. In the first, the derivative of a function is found to be undefined at x equals three, indicating a relative extrema at that point. The second example involves finding the derivative of a function and setting it to zero to solve for x. The derivative involves a square root and is set to zero, leading to a solution of x being the cube root of 25. Additionally, it is noted that the derivative is undefined at x equals zero, which also indicates a relative extrema. The paragraph concludes by stating that the nature of these extrema (whether they are maxima or minima) will be determined in a future lesson.
Mindmap
Keywords
💡Relative extrema
💡Local minima
💡Local maxima
💡Critical values
💡First derivative
💡Undefined derivative
💡Graph
💡Hilltop
💡Valley bottom
💡Derivative
💡Function
Highlights
Introduction to the concept of relative extrema, which includes relative minima and maxima, also known as local minima and maxima.
Explanation that a relative minimum is the lowest point within a small interval on a graph, likened to the bottom of a valley.
Illustration of a relative minimum point on a graph, emphasizing it as the lowest area in a relatively small area.
Description of a relative maximum as the highest point within a small interval on the graph, analogous to the top of a hill.
Clarification that relative extrema are not necessarily the highest or lowest points on the entire graph, only within a small part.
Method to find relative extrema by locating critical values, which are points where the first derivative is either zero or undefined.
Example calculation of the first derivative of a function and finding where it equals zero to locate a relative extrema.
Explanation that the nature of the extrema (whether it's a hilltop or valley bottom) at a critical point will be determined in a future lesson.
Demonstration of finding the first derivative of a function and identifying an undefined derivative as a potential relative extrema.
Procedure to determine if the derivative equals zero by cross-multiplying and solving for x.
Example of a function where the first derivative is undefined at a specific point, indicating a potential relative extrema.
Technique to rewrite a function and its derivative to solve for critical points, such as x to the power of three halves.
Identification of a relative extrema at the cube root of 25 and another at x equals zero due to division by zero in the derivative.
Note that the specific type of extrema (maximum or minimum) at these points will be determined in a future lesson.
Emphasis on the importance of understanding both defined and undefined first derivatives in the context of finding relative extrema.
The use of algebraic manipulation to solve for x when the derivative equals zero, as demonstrated in the examples.
Highlight of the need to factor out terms and use properties of exponents to solve for x in the derivative.
Mention of simplifying expressions, such as writing the cube root of 25 as the cube root, to make solutions more understandable.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: