Relative Extrema
TLDRThis lesson delves into the concept of relative extrema, also known as local maxima and minima, within the context of calculus. The instructor explains that relative extrema are points where a function's rate of change experiences a transition, either from increasing to decreasing or vice versa. To identify these points, the first derivative test is employed, which involves finding critical numbers where the derivative is zero or undefined. The process is demonstrated with various functions, including polynomials, products of functions, and natural logarithms. The importance of verifying results using tools like Desmos is emphasized, as it helps ensure the accuracy of the mathematical work. The lesson is practical, guiding students through the steps of differentiation, applying the first derivative test, and analyzing the behavior of the function to determine relative extrema.
Takeaways
- 📌 A relative extremum, also known as a local extremum, refers to the highest or lowest points within a certain region of a function, as opposed to the absolute highest or lowest points.
- 🔍 To identify relative extrema, one must first find critical numbers where the derivative of the function is either zero or undefined.
- 📈 The first derivative test involves checking the sign of the derivative before and after a critical number to determine if it corresponds to a relative maximum or minimum.
- 📉 If the function's behavior changes from increasing to decreasing at a critical number, it indicates a relative maximum. Conversely, a change from decreasing to increasing indicates a relative minimum.
- 🤔 It's important to verify the results algebraically and graphically, as the presence of a critical number does not always guarantee an extremum; it could also indicate a discontinuity or inflection point.
- 📐 The process for finding relative extrema involves differentiating the function, solving for the derivative equal to zero or undefined, and then analyzing the behavior of the function around the critical numbers.
- 🔢 Polynomial functions are continuous and do not have undefined derivatives, so the focus is on finding where the derivative is zero to identify critical numbers.
- 🎓 The quotient rule and product rule are essential differentiation rules used when dealing with functions that are products or quotients of other functions.
- ✅ Using tools like Desmos or a calculator can help verify the work done to find relative extrema, but it's crucial to show the algebraic process for a complete understanding.
- 📊 Graphing the function can provide a visual representation of the relative extrema and help confirm the algebraic findings.
- 🤓 Factoring is a useful technique when solving for critical numbers, especially when dealing with polynomials or products of functions.
- 🚫 It's important to remember that not all critical points will result in extrema; they must be tested to determine their nature within the function's context.
Q & A
What is a relative extremum?
-A relative extremum, also known as a local extremum, refers to a maximum or minimum value of a function within a certain region or interval. It is not necessarily the highest or lowest point of the entire function but is the highest or lowest within a local or relative region.
How are relative extrema related to critical numbers?
-Relative extrema occur at critical numbers. A critical number is a value where the derivative of the function is either zero or undefined. These points are potential locations for relative maxima or minima.
What is the first derivative test used for?
-The first derivative test is used to find relative extrema of a function. It involves finding critical numbers and then determining the behavior of the function (whether it is increasing or decreasing) around these points.
How can you identify if a critical number is a relative maximum or minimum?
-You can identify a relative maximum or minimum by testing the behavior of the function's derivative around the critical number. If the function changes from increasing to decreasing, the critical number is a relative maximum. If it changes from decreasing to increasing, it is a relative minimum.
What is the role of the second derivative in analyzing extrema?
-While the script does not explicitly mention the second derivative, in calculus, the second derivative test is often used to determine the concavity of a function and can also help in identifying whether a critical point is a maximum, minimum, or neither.
What happens when the derivative of a function is undefined?
-When the derivative of a function is undefined, it indicates a sharp turn or a vertical tangent at that point, which is known as a critical number. This can occur at points where the function has a cusp or a vertical asymptote.
How does the behavior of a function's slope relate to its increasing or decreasing nature?
-The behavior of a function's slope is directly related to whether the function is increasing or decreasing. If the slope is positive, the function is increasing; if the slope is negative, the function is decreasing.
What is the significance of factoring in finding critical numbers?
-Factoring is a method to simplify the derivative and make it easier to identify values for which the derivative equals zero. By setting each factor equal to zero, you can find the critical numbers where the function may have relative extrema.
Why is it important to verify the results using a graphing tool like Desmos?
-Verifying results using a graphing tool like Desmos ensures the accuracy of the algebraic work done to find relative extrema. It provides a visual confirmation of the function's behavior and the locations of maxima and minima.
What are the steps to apply the first derivative test to find relative extrema?
-The steps to apply the first derivative test are: 1) Find the derivative of the function. 2) Find the critical numbers by setting the derivative equal to zero or where it is undefined. 3) Determine the behavior of the function (increasing or decreasing) around the critical numbers. 4) Identify where the function changes from increasing to decreasing (indicating a relative maximum) or from decreasing to increasing (indicating a relative minimum).
How can you determine if a critical number corresponds to a discontinuity or an inflection point?
-If the function's behavior does not change from increasing to decreasing or vice versa at a critical number, it may indicate a discontinuity or an inflection point. A discontinuity would have an undefined slope, while an inflection point would have a change in concavity without a change in the direction of the slope.
Outlines
📚 Introduction to Relative Extrema
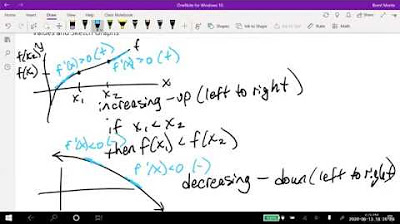
The script begins with an introduction to relative extrema, also known as local maxima and minima. These points are not necessarily the highest or lowest points on a function but are the highest or lowest within a certain region. The concept is illustrated with a graph, highlighting how relative extrema occur at critical points where the derivative is zero or undefined. The speaker emphasizes the need to identify these points mathematically, not just visually on a graph.
🔍 Identifying Critical Numbers for Extrema
The second paragraph delves into identifying critical numbers, which are the x-values where the derivative of a function is either zero or undefined. The speaker explains that while these points may not always be extrema, they are potential candidates. The concept of the first derivative test is introduced as a method to algebraically find relative extrema by analyzing the behavior of the function's derivative.
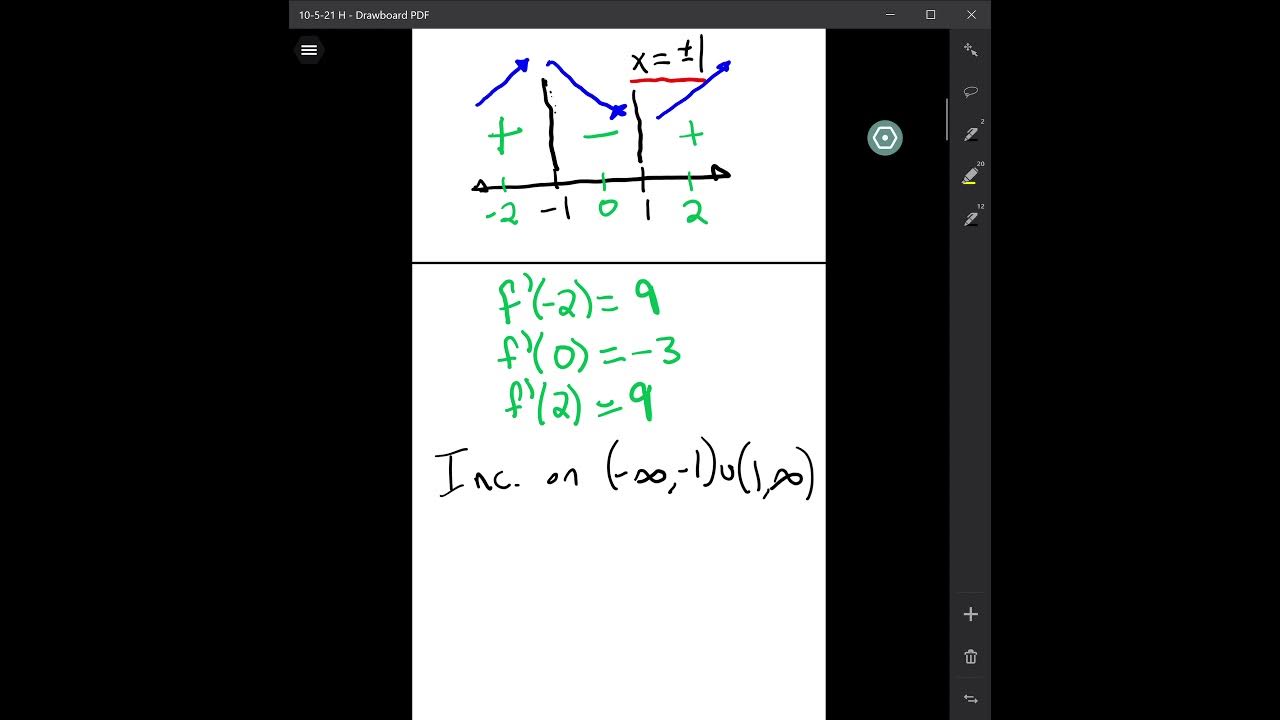
📈 Using the First Derivative Test with Polynomials
The third paragraph focuses on applying the first derivative test to a polynomial function. The process involves finding the derivative, solving for where it equals zero, and identifying critical numbers. The behavior of the derivative before and after these critical numbers is then tested to determine if they correspond to maxima or minima. The speaker demonstrates this with a specific polynomial function and uses a calculator to verify the results.
📉 Analyzing Functions with Exponential and Logarithmic Components
The fourth paragraph discusses the differentiation of functions involving exponential and logarithmic components. The speaker shows how to apply the product rule and chain rule to find the derivative of such functions. After finding the derivative, the process of identifying critical numbers and using the first derivative test to find relative extrema is demonstrated. The importance of factoring to simplify the derivative and finding critical numbers is highlighted.
🔢 Simplifying and Solving for Critical Numbers
In the fifth paragraph, the speaker continues with the process of simplifying derivatives and solving for critical numbers. They emphasize the importance of simplifying expressions to make it easier to find where the derivative equals zero or is undefined. The speaker also demonstrates how to use the quotient rule to differentiate a function involving a natural logarithm and discusses the process of finding relative extrema for this type of function.
📊 Verifying Results with Graphs
The sixth paragraph stresses the importance of verifying the work done algebraically by plotting the function on a graph. The speaker shows how to use graphing tools to confirm the presence of relative maxima and minima at the critical numbers found. They also discuss how to find the corresponding y-values for these extrema points, either by using the graph or by plugging the x-values back into the original function.
🤔 Reflecting on the Process and Common Errors
The seventh paragraph serves as a reflection on the process of finding relative extrema. The speaker acknowledges a mistake made during the calculation and emphasizes the importance of verifying all work. They discuss differentiating a function with a fraction and how to handle the power rule and the potential for an undefined derivative at certain points. The concept of an inflection point is introduced as a scenario where there is no change from increasing to decreasing, indicating no extremum.
🧐 Final Thoughts and Encouragement
In the final paragraph, the speaker wraps up the lesson by reminding the audience to think of maxima as peaks and minima as valleys. They acknowledge the complexity of the topic and the challenges faced during the explanation, attributing some confusion to the presence of extra dogs in their house. The speaker encourages students to reach out if they have questions and looks forward to the next lesson.
Mindmap
Keywords
💡Relative extrema
💡Critical numbers
💡Derivative
💡First derivative test
💡Quotient rule
💡Chain rule
💡Product rule
💡Natural logarithm
💡Exponential function
💡Inflection point
💡Continuity
Highlights
A relative extremum, also known as a local extremum, refers to the highest or lowest points within a certain region of a function.
Relative extrema can be identified as maximums or minimums within a local or relative region of a function's graph.
Critical numbers, where the derivative is zero or undefined, often coincide with relative extrema.
The first derivative test is used to find relative extrema by analyzing the behavior of the function's derivative.
A change from increasing to decreasing in the function's graph indicates a relative maximum at the critical number.
Conversely, a change from decreasing to increasing indicates a relative minimum.
If there's no change in the function's behavior around a critical number, it may indicate a discontinuity or inflection point instead of an extremum.
The process of finding relative extrema involves algebraic techniques, including finding the derivative of the function and solving for critical numbers.
The use of technology, such as calculators or software like Desmos, can assist in verifying the work done to find relative extrema.
For polynomial functions, finding the derivative and setting it to zero allows for solving the quadratic equation to find critical numbers.
The behavior of the derivative (positive or negative) determines whether the function's graph is increasing or decreasing.
The product rule and chain rule are essential for differentiating more complex functions, such as those involving multiplication and exponentials.
Factoring is a useful technique for simplifying derivatives and finding critical numbers, especially in the case of polynomials.
Exponential functions never reach zero, which means they do not produce critical numbers where the derivative is zero.
The quotient rule is applied when differentiating functions involving fractions, which can lead to finding relative extrema.
It's crucial to verify the results of algebraic work by graphing the function to ensure the accuracy of identified relative extrema.
Mistakes can occur during calculations, emphasizing the importance of checking work and using graphing tools for confirmation.
Functions with no real solutions for their derivatives equal to zero or undefined do not have relative extrema within the real number domain.
The concept of relative extrema is integral to calculus and helps in understanding the behavior of functions within specific intervals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: