Second Derivative Test Multivariable (Calculus 3)
TLDRThis video from Houston Math Prep explains the concept of local maxima and minima for functions of two variables. It introduces the second derivative test to classify critical points as local maxima, minima, or saddle points. The script walks through finding critical points by setting first partial derivatives to zero and then using the determinant of the Hessian matrix to determine the nature of these points. Examples illustrate the process, emphasizing the importance of concavity in identifying extrema.
Takeaways
- 📚 The second derivative test is used for functions of two variables to determine local maxima, minima, or saddle points.
- 🔍 A point P in an open region of a function's domain is a local maximum if one cannot 'walk uphill' in any direction from P, and a local minimum if one can only 'walk uphill' from P.
- 📌 Critical points for functions of two variables are found where the first partial derivatives with respect to x and y are both zero or undefined.
- 🔑 The interior of a function's domain refers to points not on the boundary of the domain, which is crucial for identifying critical points.
- 🧭 The second derivative test involves calculating the determinant of a 2x2 matrix of second partial derivatives, known as the Hessian matrix.
- 📉 A negative determinant (D) indicates a saddle point, where the surface curves upward in some directions and downward in others.
- ⬆️ A positive determinant with both pure second derivatives (Fxx and Fyy) positive indicates a local minimum, as the surface is concave up in both x and y directions.
- ⬇️ A positive determinant with both pure second derivatives negative indicates a local maximum, as the surface is concave down in both directions.
- 🔄 If the determinant is zero, the second derivative test is inconclusive, and the nature of the critical point cannot be determined using this method alone.
- 📘 Examples are provided to illustrate the process of finding critical points and applying the second derivative test to classify them as local maxima, minima, or saddle points.
- 👍 The video concludes with a summary of how to use the second derivative test to determine the nature of critical points for functions of two variables.
Q & A
What is the definition of a local maximum for a function of two variables?
-A local maximum for a function of two variables occurs at a point P in an open region of the domain if, from P, you cannot walk uphill in any direction on the graph, implying there is no direction from P where the function value increases immediately.
How is a local minimum different from a local maximum for functions of two variables?
-A local minimum is the opposite of a local maximum. At a local minimum, you cannot walk downhill immediately in any direction from the point P on the graph, meaning you can only walk uphill no matter which direction you choose.
What is a critical point in the context of functions of one variable?
-In the context of single-variable calculus, a critical point occurs where the first derivative of the function is zero or undefined. These points are candidates for local maxima or minima but are not guaranteed to be either.
Why is it important that a critical point be an interior point for functions of one variable?
-An interior point is important because it excludes endpoints when considering local extrema on a closed interval. The function's behavior at the endpoints can be different from the interior, and local extrema are typically analyzed within the open interval.
What are the conditions for a point to be a critical point for functions of two variables?
-For functions of two variables, a point is a critical point if both the partial derivatives with respect to each variable (∂f/∂x and ∂f/∂y) are zero or at least one of them is undefined, and the point is in the interior of the domain.
Can you explain what is meant by the 'interior' of a function of two variables?
-The 'interior' of a function of two variables refers to the region within the domain of the function where the function is defined, excluding the boundaries or edges of the domain.
What is a saddle point in the context of functions of two variables?
-A saddle point is a critical point where the function does not have a local maximum or minimum. At a saddle point, there are directions in which the function increases (uphill) and directions in which it decreases (downhill) immediately from that point.
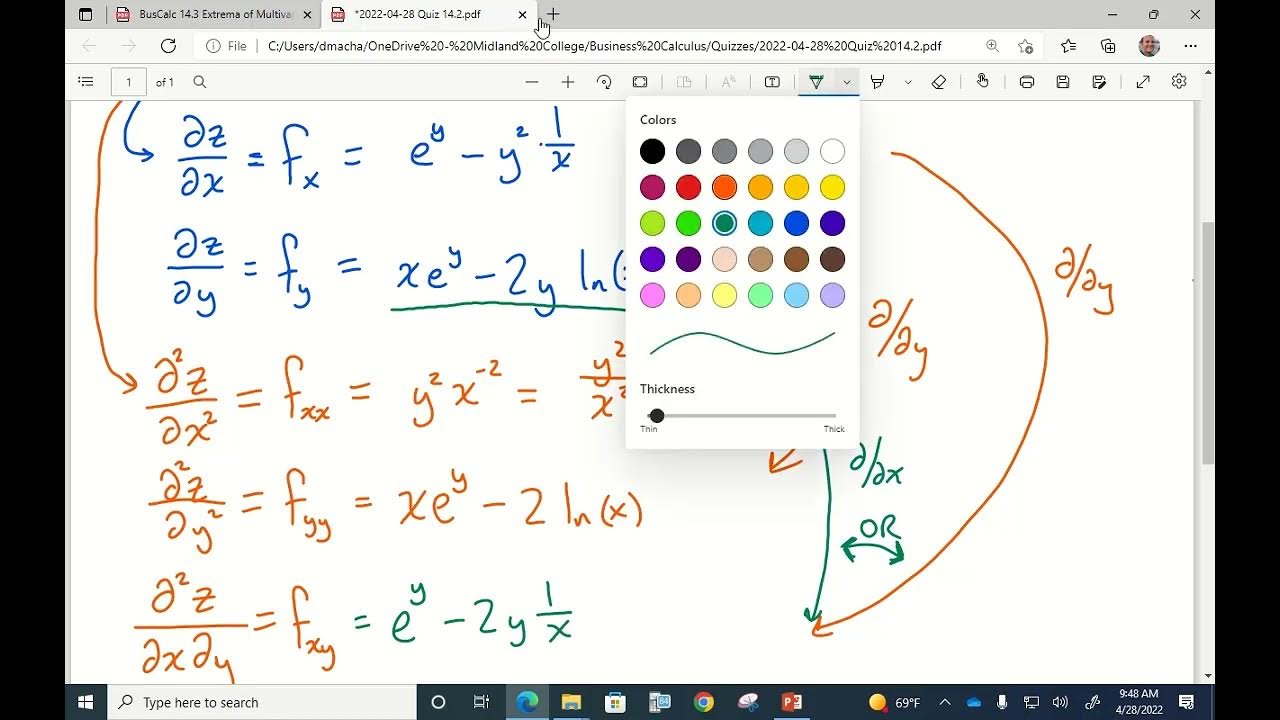
What is the Hessian matrix, and how is it used in the second derivative test for functions of two variables?
-The Hessian matrix is a square matrix of second-order partial derivatives for a function of two variables. It is used in the second derivative test to classify critical points as local maxima, minima, or saddle points by evaluating the determinant of this matrix and the signs of the pure second partial derivatives.
How does the sign of the determinant D in the second derivative test help determine the nature of a critical point?
-If the determinant D is negative, the critical point is a saddle point. If D is positive, the nature of the critical point depends on the signs of the pure second partial derivatives: if they are both positive, it's a local minimum; if both are negative, it's a local maximum. If D equals zero, the test is inconclusive.
Can you provide an example of how to find and classify critical points for a function of two variables using the second derivative test?
-Sure. For the function f(x, y) = x^3 - 3x - y^2 + 4y, first find the first partial derivatives ∂f/∂x and ∂f/∂y, set them to zero to find critical points, then compute the second partial derivatives to form the Hessian matrix. Calculate the determinant D and the signs of the pure second partial derivatives to classify each critical point using the second derivative test.
Outlines
📚 Introduction to Second Derivatives and Local Extrema
This paragraph introduces the concept of second derivatives and their use in identifying local maxima and minima for functions of two variables. The instructor explains the idea of a local maximum as a point from which one cannot 'walk uphill' in any direction on the graph, and a local minimum as the opposite. The paragraph also revisits the process of finding local extrema in single-variable calculus, emphasizing the role of critical points and the use of first and second derivative tests. The transition to functions of two variables is discussed, with a focus on finding points in the interior of the domain where both partial derivatives are zero or undefined, which are potential critical points.
🔍 Critical Points and Interior Points in Functions of Two Variables
The paragraph delves into the specifics of identifying critical points for functions of two variables. It explains the concept of 'interior' points in the domain of a function, using the example of an upper hemisphere to illustrate where the interior lies. The process of finding critical points involves setting the first partial derivatives with respect to x and y to zero. The paragraph also introduces the idea of a saddle point, a critical point where the surface curves in different directions, allowing one to 'walk uphill' and 'walk downhill' from the same point, and contrasts this with local maxima and minima.
📈 Second Derivative Test for Functions of Two Variables
This section introduces the second derivative test for functions of two variables, which helps classify critical points as local maxima, minima, or saddle points. The test involves calculating a determinant, denoted as D, from a 2x2 matrix of second partial derivatives. The sign of D, along with the signs of the pure second partial derivatives, determines the nature of the critical point. A negative D indicates a saddle point, while a positive D suggests further analysis based on the pure second derivatives' signs to determine if the point is a local maximum or minimum. The Hessian matrix, which contains the second partial derivatives, is also mentioned.
📘 Applying the Second Derivative Test with Examples
The paragraph provides a step-by-step application of the second derivative test using specific examples. It demonstrates how to find critical points by setting the first partial derivatives to zero and then classifying these points using the second derivative test. The examples include functions with variables x and y, where the process of finding second partial derivatives and calculating the determinant D is shown. The results of the test for each critical point are discussed, indicating whether they are local maxima, minima, or saddle points.
🔑 Conclusion on Finding Local Extrema and Saddle Points
The final paragraph wraps up the discussion on finding and classifying local extrema and saddle points in functions of two variables. It reiterates the process of using the second derivative test to determine the nature of critical points. The importance of identifying the correct critical points and the conditions under which the second derivative test provides conclusive results are highlighted. The paragraph concludes with a summary of the insights gained from the examples and encourages further practice with these concepts.
Mindmap
Keywords
💡Second Derivative
💡Local Maxima and Minima
💡Critical Point
💡Interior Point
💡Partial Derivatives
💡Hessian Matrix
💡Saddle Point
💡Concavity
💡Discriminant (D)
💡Mixed Partial Derivatives
Highlights
Introduction to the concept of local maxima and minima for functions of two variables.
Explanation of how to determine if a point is a local maximum or minimum by 'walking uphill' or 'downhill' on the graph.
The importance of finding critical points where the first partial derivatives are zero or undefined.
The requirement for critical points to be interior points, not on the boundary of the domain.
Illustration of the interior of a function using an upper hemisphere example.
Demonstration of how to calculate partial derivatives for a function of two variables.
Identification of critical points by setting partial derivatives equal to zero and solving for variables.
Introduction of the second derivative test for functions of two variables to classify critical points.
Explanation of the Hessian matrix and its role in the second derivative test.
Criteria for determining a saddle point using the second derivative test.
Description of the conditions for a local minimum based on positive second partial derivatives.
Conditions for identifying a local maximum with negative second partial derivatives.
The inconclusive result of the second derivative test when the determinant D equals zero.
Application of the second derivative test to a function with an example to find and classify critical points.
Detailed walkthrough of classifying critical points as saddle points, local maxima, or local minima.
Example of a function with multiple critical points, some of which are saddle points.
Final summary of the process for determining local extrema and saddle points for functions of two variables.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: