AP Precalculus Practice Exam Question 27

NumWorks
23 May 202303:51
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter discusses the motion of a bicycle pedal in a physical therapy center, which simulates a patient's exercise. The pedal's height above the ground is modeled using a sine function, with the amplitude determined by the pedal's arm length of 8 inches. The frequency is derived from the pedal's one revolution per second, leading to a formula involving a sine function with a period of 2Ο€. The correct expression for the height H(T) of the pedal at time T seconds is identified as option D, which includes the amplitude, frequency, and midline height of 12 inches.

Takeaways
  • 🚴 The context is a physical therapy center with a bike for patient exercise.
  • πŸ”„ The bicycle pedal's height above the ground periodically increases and decreases.
  • ⏱ At time T=0 seconds, the pedal's height is at 12 inches above the ground.
  • πŸ”„ The pedal's motion is circular, defined by an 8-inch arm.
  • πŸŽ› The patient's pedal completes one revolution per second.
  • πŸ“Š The problem involves identifying a mathematical expression for the height of the pedal at time T.
  • πŸ“ The model for the motion is a sine function, as suggested by options A, B, C, and D.
  • πŸ”§ The amplitude of the sine function is determined by the pedal arm's length, which is 8 inches.
  • πŸ”„ The sine function's negative value indicates the direction of the motion relative to the wheel's midline.
  • πŸŒ€ The frequency of the sine function is calculated as 2Ο€ over the period, which is 1 revolution per second.
  • 🎯 The correct mathematical expression for the height H(T) is identified as option D, which incorporates amplitude, frequency, and midline.
Q & A

  • What is the initial height of the bicycle pedal above the ground level at time T equals zero seconds?

    -The initial height of the bicycle pedal above the ground level at time T equals zero seconds is 12 inches.

  • What is the length of the pedal arm that defines the circular motion of the pedal?

    -The length of the pedal arm that defines the circular motion of the pedal is 8 inches.

  • How many revolutions per second does the patient's pedal make when in use?

    -The patient's pedal makes one revolution per second when in use.

  • What type of function is suggested by the options provided for modeling the height of the bicycle pedal above the ground level?

    -The options provided suggest using a sine function to model the height of the bicycle pedal above the ground level.

  • What is the role of the amplitude in the sine function for this scenario?

    -The amplitude in the sine function represents the maximum height the pedal can reach above and below the midline of the wheel's motion.

  • What is the midline of the wheel's motion in this context?

    -The midline of the wheel's motion is the average height of the pedal, which is 12 inches in this scenario.

  • How is the frequency of the sine function determined in this problem?

    -The frequency of the sine function is determined by the number of revolutions per second, which is 1 in this case, leading to a frequency of 2Ο€.

  • What is the significance of the phase shift in the sine function, and why is it not present in this scenario?

    -The phase shift in a sine function indicates a horizontal shift of the function. It is not present in this scenario because the pedal starts at its midline position at time T equals zero seconds.

  • What is the correct expression for H of T, the height of the bicycle pedal above the ground level at time T, based on the script?

    -The correct expression for H of T is given by option D, which is 12 - 8 * sin(2Ο€ * T).

  • Why is the amplitude negative in the sine function expression provided in the script?

    -The amplitude is negative in the sine function expression because the pedal's height decreases from the midline as the sine function goes negative, indicating a downward movement from the midline.

  • What does the argument of the sine function represent in this context?

    -The argument of the sine function, which is 2Ο€ * T, represents the angular position of the pedal in its circular motion at any given time T.

Outlines
00:00
πŸš΄β€β™‚οΈ Bicycle Pedal Motion Analysis

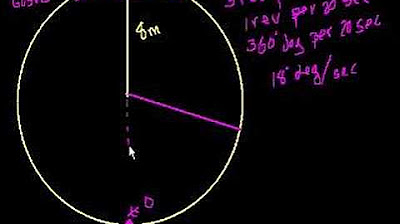
The script discusses a physical therapy scenario involving a bicycle with a pedal that oscillates in height. At time T=0, the pedal is positioned 12 inches above the ground. The pedal's motion is circular, facilitated by an 8-inch arm attached to it, revolving at a rate of one revolution per second. The script delves into the mathematical modeling of this motion, suggesting a sine function as the model. It explains the components of the sine function, including amplitude, frequency, and midline, and identifies the correct expression for the height H of the pedal at any time T as option D, which is a sine function with an amplitude of 8, a frequency of 2Ο€ (since the period is 1 second), and a midline of 12 inches.

Mindmap
Keywords
πŸ’‘Physical Therapy
Physical therapy is a method of treatment that involves physical exercises and other non-medical means to help patients restore, maintain, or improve their physical abilities. In the video's context, it refers to the use of a bicycle for exercise, which is a common physical therapy tool to improve mobility and strength.
πŸ’‘Bicycle Pedal
The bicycle pedal is the part of the bicycle that the rider pushes against to propel the bike forward. In the video, the height of the pedal above the ground is a key factor in the exercise, as it periodically increases and decreases to provide a dynamic workout.
πŸ’‘Height
Height, in this context, refers to the vertical distance of the bicycle pedal from the ground level. The script discusses how the height changes as the pedal moves in a circular motion, which is essential for understanding the exercise's mechanics.
πŸ’‘Trigonometric Functions
Trigonometric functions, such as sine, are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the video, sine functions are used to model the periodic motion of the bicycle pedal, with the amplitude and frequency determining the extent and speed of the motion.
πŸ’‘Amplitude
Amplitude in the context of the video refers to the maximum extent of the pedal's movement above and below the midline. It is determined by the length of the pedal's arm, which is eight inches, and it dictates how high and low the pedal can go in its circular motion.
πŸ’‘Midline
The midline is the central position of the pedal's circular motion, which is at a height of 12 inches above the ground. It serves as the reference point for the amplitude and is crucial for understanding the starting position of the pedal's movement.
πŸ’‘Frequency
Frequency in the video refers to the number of revolutions the pedal makes per second. With one revolution per second, the frequency is calculated as 2Ο€ (since the period is one second), indicating how often the pedal completes a full cycle.
πŸ’‘Phase Shift
Phase shift is a concept in trigonometry that refers to the horizontal displacement of a function. In the video, there is no phase shift mentioned, indicating that the motion of the pedal starts at the midline and does not have any horizontal offset.
πŸ’‘Period
The period is the time it takes for a repeating event to reoccur. In the script, the period is one second, as the pedal completes one revolution per second, which is used to calculate the frequency.
πŸ’‘Sine Function
The sine function is a type of trigonometric function that models periodic phenomena. In the video, the sine function is used to describe the height of the bicycle pedal as a function of time, with the amplitude, frequency, and midline incorporated into the function to accurately represent the pedal's motion.
πŸ’‘Expression
In the context of the video, an expression refers to the mathematical formula used to describe the height of the bicycle pedal at any given time. The correct expression, as identified in the script, is a sine function with specific amplitude, frequency, and midline values that match the pedal's motion.
Highlights

The physical therapy center has a bike with a pedal that periodically increases and decreases in height above the ground.

The height of the pedal above the ground at time T=0 seconds is 12 inches.

The pedal's 8-inch arm defines the circular motion of the pedal.

The patient's pedal revolves one revolution per second.

The sine function is used to model the height of the bicycle pedal above the ground level at time T.

The amplitude of the sine function determines how high and low the pedal can go above and below the wheel.

The amplitude is 8 inches, based on the length of the pedal arm.

The midline of the wheel motion is at 12 inches, which is the middle value of the rotation.

The frequency of the sine function is calculated as 2Ο€ divided by the period (1 second).

The correct expression for the height H(T) is given by option D: 12 - 8sin(2Ο€T).

The sine function model accounts for the periodic increase and decrease in pedal height.

The model has no phase shift, as indicated by the absence of a phase term in the sine function.

The model's midline is explicitly stated as 12 inches, not variable K.

The amplitude of 8 inches represents the maximum height above and below the midline.

The frequency of 2Ο€ accounts for the one revolution per second of the pedal.

The sine function correctly captures the circular motion of the pedal arm.

The model is chosen based on the given parameters and the observed behavior of the pedal.

The correct answer is identified through a process of elimination and comparison with the given options.

Transcripts

Browse More Related Video

Ferris Wheel MHF4U Modelling Trigonometric Functions Test

Ferris Wheel Trig Problem

Ferris Wheel Trigonometry Problem

Ferris Wheel problem for Precalculus

Sine & Cosine Graphs Word Problems (Writing the Equation)

Ferris Wheel Trigonometry Periodic Functions Multiple Choice Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physical TherapyBicycle ExerciseTrigonometric ModelSine FunctionOscillationAmplitudeFrequencyHealthcare TechnologyMotion AnalysisPatient Rehabilitation