Ferris Wheel Trigonometry Periodic Functions Multiple Choice Test
TLDRIn this educational video, Anil Kumar introduces viewers to the application of trigonometry with a focus on a Ferris wheel's height function, modeled by H(t) = 20 - 18sin(2π/3(t - 1)) meters. He guides the audience through sketching the graph and solving seven multiple-choice questions without a calculator. The questions cover finding the basket's height at 75 seconds, determining when it reaches 20 meters, identifying the maximum height, and calculating time for full rotations, among others. Anil emphasizes the importance of graph sketching for quick problem-solving and encourages viewers to engage with the content for a deeper understanding of trigonometric concepts.
Takeaways
- 📚 The video discusses the application of trigonometry, specifically focusing on a Ferris wheel problem with multiple-choice questions.
- 📉 The height of the basket on the Ferris wheel is modeled by the function H(t) = 20 - 18 sin(2π/3 t - 1), where H(t) is in meters and t is in minutes.
- 📝 The video encourages viewers to pause and sketch the graph of the function before proceeding to the multiple-choice questions.
- 🔍 The parameters of the sine function are identified: the axis is 20, amplitude is 18, and the time period is 3 minutes.
- 📈 The maximum and minimum heights of the basket are calculated as 38 meters and 2 meters, respectively.
- 📊 The video provides a method to sketch the sine wave graph without a calculator, emphasizing the importance of understanding the function's behavior.
- ⏱ The video explains how to find specific values such as the height of the basket after 75 seconds and when the basket is at a certain height.
- 🔄 The time it takes for the basket to complete three full rotations is calculated to be 9 minutes.
- 📏 The distance traveled by the basket in 2 minutes is derived to be 24π meters.
- 🔄 The angular velocity of the basket is determined to be π/90 radians per second.
- 👍 The video concludes by emphasizing the importance of sketching the function for a clear understanding and easier problem-solving.
Q & A
What is the function modeling the height of the basket on the Ferris wheel?
-The function modeling the height of the basket on the Ferris wheel is \( H(t) = 20 - 18 \sin(\frac{2\pi}{3}(t - 1)) \), where \( H(t) \) is the height above the ground in meters and \( t \) is time in minutes.
What is the amplitude of the sine function in the model?
-The amplitude of the sine function in the model is 18 meters, which represents the maximum distance the basket moves above and below the axis of rotation.
What is the axis of rotation in the context of this Ferris wheel model?
-The axis of rotation in the context of this Ferris wheel model is at a height of 20 meters above the ground, as indicated by the constant term in the function.
What is the time period of the Ferris wheel's rotation according to the model?
-The time period of the Ferris wheel's rotation, according to the model, is 3 minutes, which is derived from the coefficient of \( t \) in the sine function, \( \frac{2\pi}{3} \).
What is the maximum height the basket reaches above the ground?
-The maximum height the basket reaches above the ground is 38 meters, which is calculated by adding the amplitude to the axis of rotation (20 + 18 = 38 meters).
What is the minimum height the basket reaches above the ground?
-The minimum height the basket reaches above the ground is 2 meters, which is calculated by subtracting the amplitude from the axis of rotation (20 - 18 = 2 meters).
How do you find the time when the basket is 20 meters above the ground?
-The basket is 20 meters above the ground when the sine function equals zero. In the model, this occurs when \( t - 1 = 0 \), which means \( t = 1 \) minute.
When does the basket reach its maximum height?
-The basket reaches its maximum height at the peak of the sine wave, which occurs at \( t = 3.25 \) minutes, or after three full and one-quarter rotations.
How much time does it take for the basket to complete three full rotations?
-It takes 9 minutes for the basket to complete three full rotations, as each rotation takes 3 minutes.
What is the distance traveled by the basket in 2 minutes?
-The distance traveled by the basket in 2 minutes is \( 24\pi \) meters, which is \( \frac{2}{3} \) of the distance covered in one full rotation (since 2 minutes is \( \frac{2}{3} \) of 3 minutes).
What is the angular velocity of the basket in radians per second?
-The angular velocity of the basket is \( \frac{\pi}{90} \) radians per second, calculated by converting the 2π radians per 3 minutes to radians per second by multiplying by \( \frac{60}{3} \).
Why is it important to sketch the graph of the function when solving these problems?
-Sketching the graph of the function is important because it provides a visual representation of the Ferris wheel's motion, making it easier to understand the problem and answer questions about the height, time, and distance without needing to perform complex calculations.
How can one solve these problems without a calculator, as suggested for IB students?
-One can solve these problems without a calculator by using mental math, estimation, and understanding of special triangle values for sine. For example, knowing that \( \sin(\frac{\pi}{6}) = \frac{1}{2} \) can simplify the calculation of the basket's height at a specific time.
Outlines
📐 Introduction to Ferris Wheel Trigonometry Problem
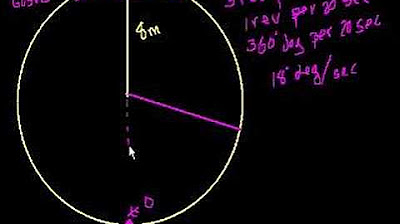
Anil Kumar introduces a trigonometry problem involving a Ferris wheel's height model. He mentions the upcoming multiple-choice questions based on this concept and encourages viewers to sketch the graph of the function \( H(T) = 20 - 18 \sin(\frac{2\pi}{3}(T - 1)) \) before attempting the questions. He provides a brief overview of the problem parameters: the axis at 20 meters, amplitude of 18 meters, and a time period of 3 minutes. Kumar emphasizes solving without a calculator, especially for IB students.
📝 Answering the Multiple-Choice Questions
Kumar begins solving the multiple-choice questions based on the Ferris wheel problem. For the first question, he calculates the height of the basket at 75 seconds (1.25 minutes), finding it to be 11 meters. For the second question, he determines that the basket is 20 meters above the ground at \( T = 1 \) minute. The third question reveals the maximum height of the basket is 38 meters, and the fourth question shows the basket reaches its maximum height at 3.25 minutes. He calculates the basket takes 9 minutes for three full rotations in question five. For the sixth question, Kumar finds the distance traveled by the basket in 2 minutes to be \( 24\pi \) meters. Finally, for the seventh question, he determines the angular velocity of the basket to be \( \frac{\pi}{90} \) radians per second.
📊 Graphing the Ferris Wheel Function for Clarity
Kumar stresses the importance of sketching the graph of the Ferris wheel function to understand and answer the questions effectively. He revisits the initial parameters and explains the sine wave's behavior, noting the shift and negative sign. He sketches the function, marking the minimum, maximum, and axis values, and emphasizes how this visual aid simplifies answering the multiple-choice questions. Kumar concludes by encouraging viewers to use sketches to grasp the problem's structure better, aiding in accurate and efficient problem-solving.
Mindmap
Keywords
💡Trigonometry
💡Ferris Wheel
💡Multiple-Choice Questions
💡Height Above Ground
💡Amplitude
💡Time Period
💡Graph Sketching
💡Angular Velocity
💡Distance Traveled
💡Special Triangle
Highlights
Anil Kumar introduces a popular application of trigonometry involving a Ferris wheel problem modeled by the function H(t) = 20 - 18sin(2π/3(t - 1)).
The function represents the height of a basket on a Ferris wheel above the ground in meters as a function of time in minutes.
Seven multiple-choice questions are based on this concept, covering various aspects of the problem.
The axis of the function is 20, which is the average height of the basket above the ground.
The amplitude is 18, indicating the maximum distance the basket moves from the axis.
The time period is 3 minutes, which is the time taken for one complete rotation of the basket.
The maximum height of the basket is 38 meters, calculated by adding the axis and amplitude.
The minimum height is 2 meters, found by subtracting the amplitude from the axis.
A method to sketch the graph of the function without a calculator is demonstrated.
The significance of the phase shift (t - 1) is explained, affecting the starting point of the sine wave.
The height of the basket after 75 seconds is calculated using the function and knowledge of special triangles.
The time when the basket is 20 meters above the ground is determined to be at 1 minute.
The maximum height of 38 meters is reached at 3.25 minutes, corresponding to the peak of the sine wave.
The time for three full rotations of the basket is calculated to be 9 minutes.
The distance traveled by the basket in 2 minutes is derived to be 24π meters.
The angular velocity of the basket is calculated to be π/90 radians per second.
The importance of sketching the function for understanding and solving the multiple-choice questions is emphasized.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: