Ferris Wheel Trig Problem
TLDRThe video script details a mathematical problem involving Jacob and Emily riding a 16-meter diameter Ferris wheel in Billings, Montana. The wheel turns at a rate of 3 revolutions per minute, and the height of the riders above the ground is modeled as a sinusoidal function of time, with the lowest point at 1 meter above ground level. The script explains how to derive the equation for their height 'h' as a function of time 't' in seconds, considering the wheel's rotation speed and the geometry of the situation. The final equation is h = 9 - 8cos(18t), which represents the height in meters as a function of time in seconds, and the script promises to graph this function in a subsequent video.
Takeaways
- 🎪 Jacob and Emily are riding a Ferris wheel at a carnival in Billings, Montana.
- 🔵 The Ferris wheel has a diameter of 16 meters, which means its radius is 8 meters.
- 📏 The lowest point of the Ferris wheel is 1 meter above the ground.
- ⏱ The Ferris wheel completes 3 revolutions per minute, equating to 18 degrees per second.
- 📉 The height h of Jacob and Emily above the ground is described as a sinusoidal function of time.
- ⏳ At t = 0, they are at the lowest point of the Ferris wheel.
- 📐 The problem involves calculating the height h as a function of time t in seconds.
- 📈 The Ferris wheel's rotation speed is converted into degrees per second to relate it to the sinusoidal function.
- 📊 The height h is determined using trigonometric relationships, specifically cosine, in relation to the angle of rotation.
- 🧩 The final equation for h as a function of t is h = 9 - 8cos(18t).
- 📊 The next step is to graph the function h = 9 - 8cos(18t) to visualize the sinusoidal motion.
Q & A
What is the diameter of the Ferris wheel that Jacob and Emily are riding?
-The diameter of the Ferris wheel is 16 meters.
What is the radius of the Ferris wheel?
-The radius of the Ferris wheel is half of its diameter, which is 8 meters.
At what height is the lowest point of the Ferris wheel above the ground?
-The lowest point of the Ferris wheel is 1 meter above the ground.
How many revolutions per minute does the Ferris wheel make?
-The Ferris wheel makes 3 revolutions per minute.
What is the relationship between the number of revolutions and the angle covered per second?
-Since the Ferris wheel makes 3 revolutions per minute, it covers 360 degrees per 20 seconds, which simplifies to 18 degrees per second.
What is the sinusoidal function of time that represents Jacob and Emily's height above the ground?
-The sinusoidal function representing their height h above the ground as a function of time t is h(t) = 9 - 8cos(18t).
Why is the cosine function used to relate the height to the angle?
-The cosine function is used because it relates the adjacent side (9 - h) to the hypotenuse (8 meters) in a right-angled triangle, which is formed by the height, radius, and the angle of rotation.
What is the significance of the number 18 in the equation h(t) = 9 - 8cos(18t)?
-The number 18 represents the rate of change in degrees per second, which is derived from the Ferris wheel's speed of 3 revolutions per minute.
What is the initial height of Jacob and Emily above the ground when t equals 0?
-At t equals 0, which is the lowest point on the wheel, their height above the ground is 1 meter plus the radius of the Ferris wheel, which is 9 meters.
How does the height of Jacob and Emily change as they ride the Ferris wheel?
-Their height changes sinusoidally with time, increasing and decreasing as they move around the Ferris wheel, following the equation h(t) = 9 - 8cos(18t).
What will be the next step after deriving the equation for h(t)?
-The next step mentioned in the script is to graph the function h(t) to visualize how the height changes over time as Jacob and Emily ride the Ferris wheel.
Outlines
🎡 Jacob and Emily's Ferris Wheel Ride
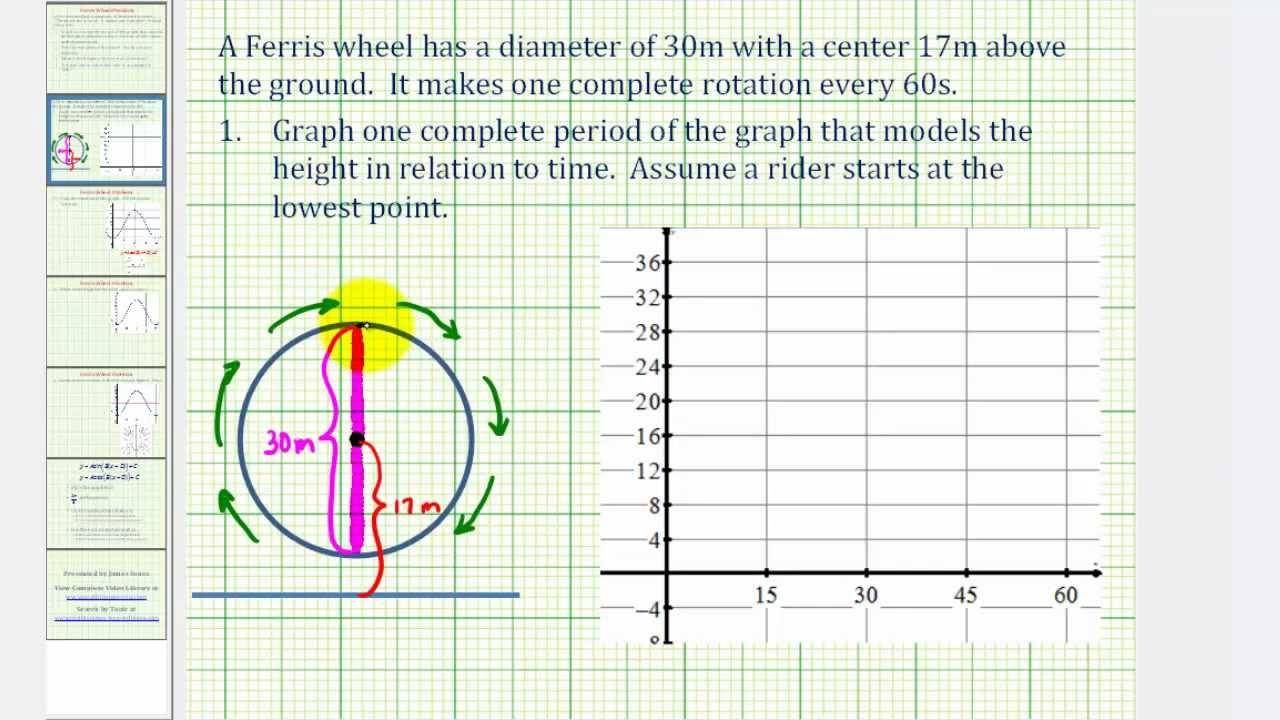
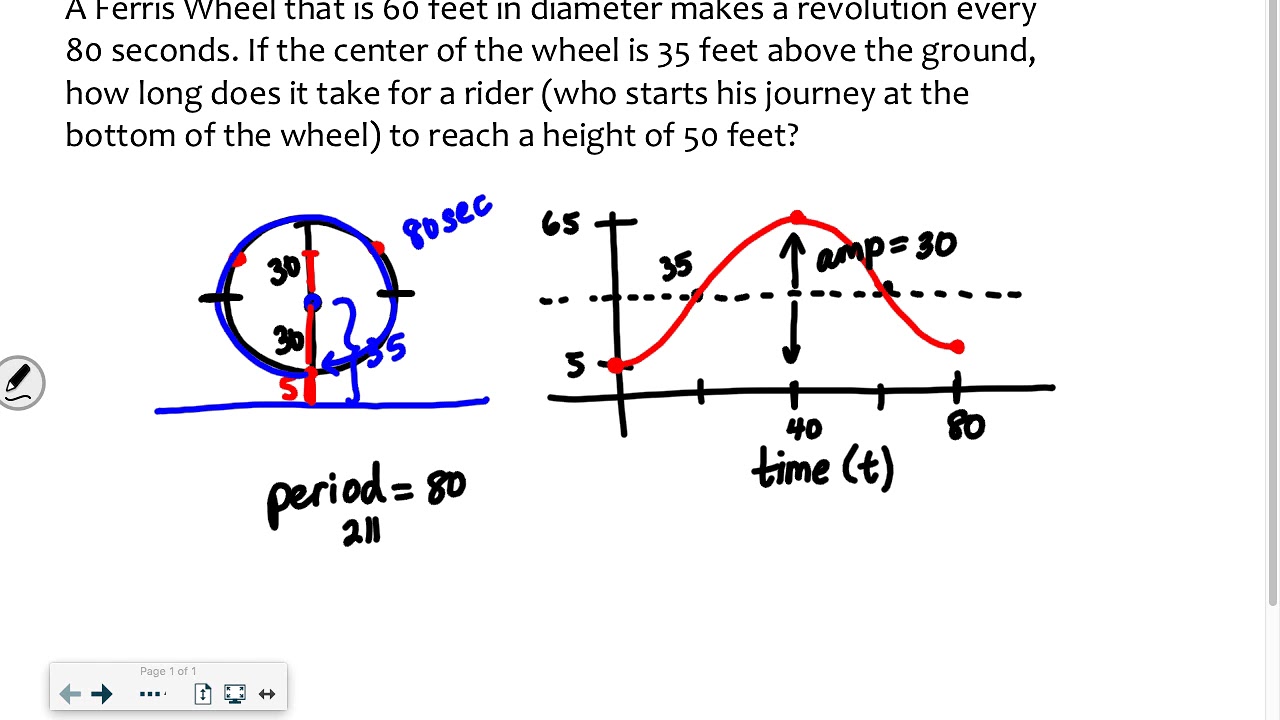
The script describes a scenario where Jacob and Emily are riding a ferris wheel at a carnival in Billings, Montana. The wheel has a diameter of 16 meters, which means its radius is 8 meters. The lowest point of the wheel is 1 meter above the ground. The height of Jacob and Emily above the ground, denoted as 'h', is said to be a sinusoidal function of time 't', with 't=0' representing the lowest point on the wheel. The wheel turns at a rate of 3 revolutions per minute, which translates to 18 degrees per second. The script aims to derive an equation for 'h' as a function of 't', given in seconds.
📚 Deriving the Height Function for the Ferris Wheel Ride
In this paragraph, the script explains the process of deriving the mathematical function for the height 'h' of Jacob and Emily on the ferris wheel as a function of time 't'. It starts by establishing that the wheel makes 3 revolutions per minute, which is equivalent to 18 degrees per second. The script then uses trigonometry to relate the angle of rotation to their height above the ground. By considering the right triangle formed by the radius of the wheel, the height above the ground, and the horizontal distance from the center to the edge of the wheel, the cosine function is used to express 'h'. The final equation derived is h = 9 - 8cos(18t), where 'h' is the height above the ground in meters, and 't' is the time in seconds. The script concludes with the intention to graph this function in the next video.
Mindmap
Keywords
💡Ferris Wheel
💡Diameter
💡Radius
💡Sinusoidal Function
💡Time (t)
💡Revolutions Per Minute (RPM)
💡Degrees
💡Trigonometric Functions
💡Hypotenuse
💡Cosine
💡Graph
Highlights
Jacob and Emily ride a ferris wheel at a carnival in Billings, Montana.
The ferris wheel has a 16-meter diameter.
Radius of the ferris wheel is half the diameter, which is 8 meters.
The lowest point of the ferris wheel is 1 meter above the ground.
Jacob and Emily's height above the ground is a sinusoidal function of time.
The ferris wheel turns at 3 revolutions per minute.
One revolution is equivalent to 360 degrees.
The ferris wheel rotates at 18 degrees per second.
The total number of degrees traveled in t seconds is 18t degrees.
The height h at any point is 1 meter plus the radius, which is 9 meters.
The height h can be expressed as a function of the angle 18t degrees.
A triangle is formed with the radius as the hypotenuse, and 9 - h as the adjacent side.
The cosine function relates the adjacent side to the hypotenuse at angle 18t degrees.
The equation for h as a function of t is derived using cosine.
The final equation for h(t) is h = 9 - 8cos(18t).
The next video will involve graphing the function h(t).
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: