Ferris Wheel MHF4U Modelling Trigonometric Functions Test
TLDRIn this educational video, Anil Kumar discusses a trigonometric function modeling problem involving a Ferris wheel with a 30-meter radius, rotating every 200 seconds. Starting 5 meters above the ground, the function H(T) is derived to represent the height above the ground over time. The equation, incorporating amplitude, phase shift, and vertical shift, is solved to find when the height exceeds 17 meters. The method involves using the cosine function, calculating the angular frequency, and applying inverse cosine to determine specific time intervals in the first three cycles where the height condition is met. The explanation is aimed at helping viewers understand how to approach and solve similar trigonometric applications.
Takeaways
- 🎢 The script discusses a problem involving a Ferris wheel with a radius of 30 meters and a height of 5 meters above the ground.
- 🔄 The Ferris wheel rotates at a rate of one revolution every 200 seconds.
- 📊 The task is to model the height of a passenger on the Ferris wheel using a trigonometric function.
- 📚 The trigonometric function is defined with an amplitude of 30 meters, a vertical shift of +35 meters (5 meters above the ground plus the radius of the wheel), and a period of 200 seconds.
- 📐 The function is written as \( H(t) = -30\cos(\frac{\pi}{100}t) + 35 \), where \( H \) is the height above the ground and \( t \) is the time in seconds.
- 🕒 The time period for one complete revolution is 200 seconds, which translates to a frequency of \( \frac{\pi}{100} \).
- 🔍 To find when the height is above a certain value, such as 17 meters, the function is set equal to that value and solved for \( t \).
- 📈 The script provides a step-by-step method to solve for the time when the height is 17 meters above the ground, using the inverse cosine function.
- ⏱ The times when the height is 17 meters above the ground are calculated to be at approximately 29.5 seconds and 170.5 seconds in the first cycle.
- 🔁 The process can be repeated for additional cycles by adding 200 seconds (the period of one cycle) to the initial times found.
- 👍 The script concludes by encouraging the viewer to understand and appreciate the method used to solve the problem.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is modeling a real-world situation, specifically the motion of a Ferris wheel, using a trigonometric function.
What is the radius of the Ferris wheel mentioned in the script?
-The radius of the Ferris wheel mentioned in the script is 30 meters.
How often does the Ferris wheel complete one revolution according to the script?
-According to the script, the Ferris wheel completes one revolution every 200 seconds.
What is the height of the Ferris wheel above the ground at the bottom of the ride?
-At the bottom of the ride, the passenger is 5 meters above the ground.
What is the amplitude of the cosine function used to model the height of the Ferris wheel?
-The amplitude of the cosine function used to model the height of the Ferris wheel is 30 meters, which is the radius of the wheel.
What is the vertical shift in the cosine function representing the height of the Ferris wheel?
-The vertical shift in the cosine function is 35 meters, which is the sum of the radius (30 meters) and the height above the ground at the bottom of the ride (5 meters).
What is the angular frequency (k value) of the cosine function used in the model?
-The angular frequency (k value) of the cosine function is π/100, calculated from 2π divided by the time period of 200 seconds.
What is the equation of the function that represents the height H above the ground at any time T?
-The equation of the function representing the height H above the ground at any time T is H(T) = -30cos(π/100T) + 35.
What is the modified question in the script regarding the height of the Ferris wheel?
-The modified question in the script asks when the height of the Ferris wheel will be above 17 meters, instead of the original 70 meters.
How does the script suggest finding the time when the height is above 17 meters for the first three cycles?
-The script suggests finding the time for the first cycle when the height is above 17 meters and then adding 200 seconds (the time period of one revolution) to find the times for the subsequent cycles.
What is the time in seconds when the height of the Ferris wheel is first above 17 meters?
-The time when the height of the Ferris wheel is first above 17 meters is approximately 29.5 seconds.
How does the script handle the symmetry of the cosine function to find additional times when the height is above 17 meters?
-The script uses the symmetry of the cosine function by finding the time when the height is above 17 meters and then calculating the corresponding time 200 seconds later (due to the 200-second revolution period) to find additional times.
Outlines
🎢 Modeling a Ferris Wheel with Trigonometric Functions
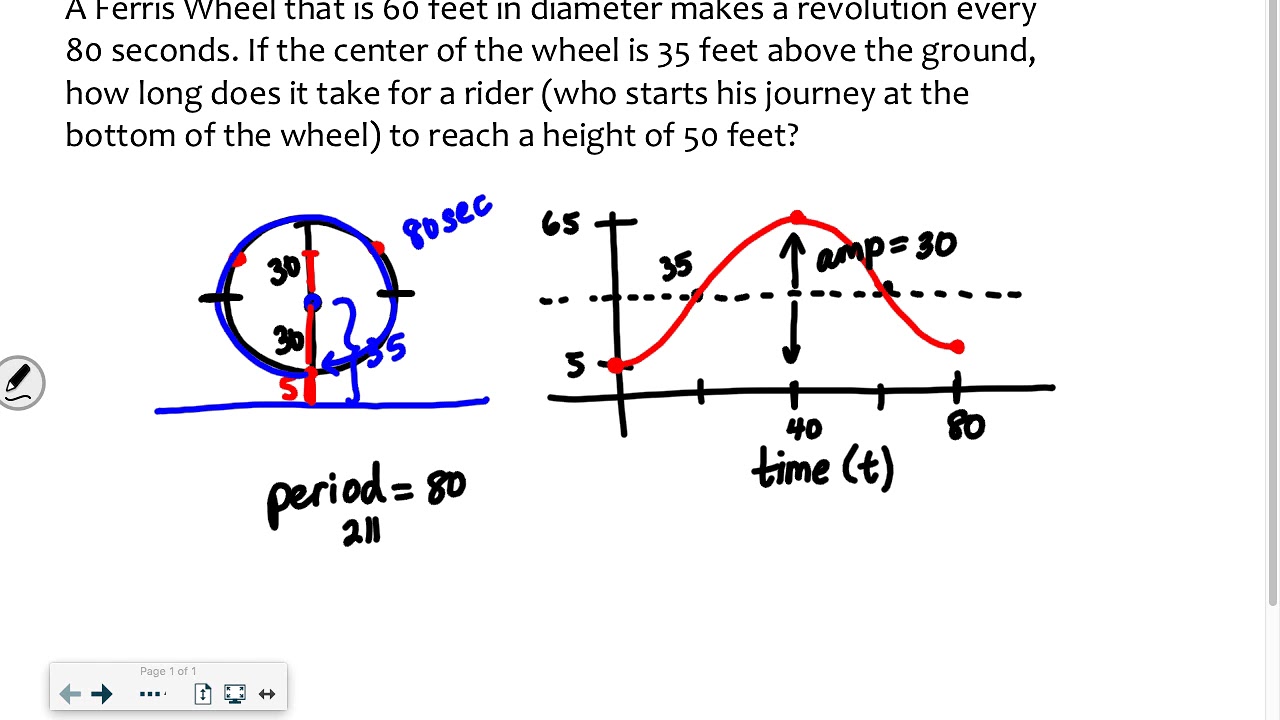
In this paragraph, Anil Kumar introduces a problem involving a Ferris wheel and the use of trigonometric functions to model its motion. The Ferris wheel has a radius of 30 meters and rotates once every 200 seconds, with passengers starting their ride 5 meters above the ground. The task is to find the trigonometric function that represents the height of a passenger above the ground at any given time 'T'. The function is derived by considering the amplitude, vertical shift, and angular frequency, resulting in the equation f(T) = -30cos(π/100T) + 35. The challenge also includes determining when the height of the wheel is above 70 meters during the first three cycles.
🕒 Calculating Time When Height is 17 Meters Above Ground
This paragraph focuses on solving for the specific times when the height of the Ferris wheel is 17 meters above the ground during the first three cycles. The equation f(T) = 17 - 30cos(π/100T) + 35 is used, which simplifies to finding the angle whose cosine is 3/5. Using the inverse cosine function, the time 'T' when the height is 17 meters is calculated to be approximately 29.5 seconds and 170.5 seconds into the cycle. By understanding the symmetry of the cosine function and the periodic nature of the Ferris wheel's rotation, additional times are found by adding 200 seconds (the period of one cycle) to these initial times, resulting in times of 229.5 seconds and 370.5 seconds. The explanation concludes with the understanding that these times are in seconds and that rounding may be necessary depending on the context of the problem.
Mindmap
Keywords
💡Trigonometric function
💡Ferris wheel
💡Radius
💡Revolutions per minute (RPM)
💡Amplitude
💡Phase shift
💡Time period
💡Angular frequency
💡Height above the ground
💡Cosine inverse
Highlights
Anil Kumar shares test questions on advanced functions for a math course.
The application question involves modeling a ferris wheel scenario with a trigonometric function.
The ferris wheel has a radius of 30 meters and rotates every 200 seconds.
Passengers start the ride 5 meters above the ground.
The task is to determine the height function H(t) representing the passenger's height over time.
The function's equation is derived from the given conditions of the ferris wheel.
The amplitude of the cosine function is set to 30 meters, the radius of the wheel.
The angular frequency k is calculated as π/100 based on the rotation period.
The vertical shift is determined to be 35 meters, accounting for the wheel's radius and the starting height.
The function f(t) is written as -30cos(π/100t) + 35 to represent the height.
The problem asks when the height is above 17 meters during the first three cycles.
The height of 17 meters is set as the condition to find the corresponding time t.
Using the derived function, the time when the height is 17 meters is calculated.
The time is found to be approximately 29.5 seconds and 170.5 seconds in the first cycle.
The symmetry of the cosine function is used to find the times in the subsequent cycles.
The times when the height is above 17 meters are listed for the first three cycles.
The solution involves understanding trigonometric functions and their applications in real-world problems.
The method demonstrates the practical use of trigonometry in modeling periodic motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: