Potential Energy Graph Example

Alison Steward
9 Dec 202009:46
EducationalLearning
32 Likes 10 Comments

TLDRThis example focuses on potential energy curves, specifically analyzing the motion of a 2-kilogram particle along the x-axis under a conservative force. The video covers determining the particle's speed at a specific point, identifying its turning point, and evaluating the force acting in a given region. By utilizing kinetic and potential energy concepts and solving related equations, the process demonstrates how to calculate total mechanical energy, particle speed, turning points, and force. Key principles like energy conservation and force as the negative slope of the potential energy graph are highlighted.

Takeaways
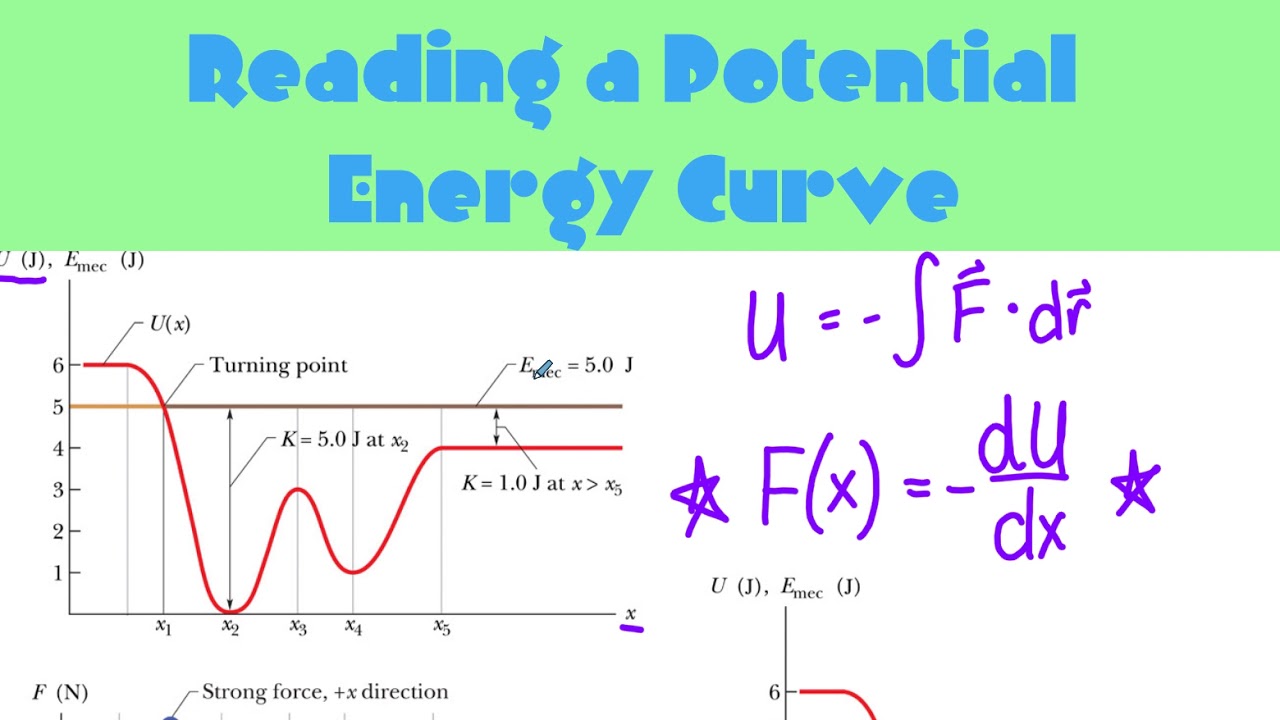
  • 📚 The script discusses an example of potential energy curves for a 2-kilogram particle moving in one dimension along an x-axis with a conservative force acting on it.
  • 📈 The potential energy associated with the force is plotted in a graph, where the particle's potential energy and kinetic energy can be determined at various points along the x-axis.
  • 🔍 The particle's velocity at x = 6.5 meters is given as negative 4 meters per second, which is used to calculate the total mechanical energy of the system.
  • 🧩 At x = 6.5 meters, the potential energy is zero, indicating that all the energy is kinetic, allowing for the calculation of the total mechanical energy as 16 Joules.
  • 🔑 To find the particle's speed at x = 4.5 meters, the script uses the total mechanical energy and the potential energy at that point to calculate the kinetic energy and subsequently the velocity, resulting in 3 meters per second.
  • 📍 The particle's turning point is located using a geometric approach comparing triangles on the potential energy graph, with the turning point found to be at 1.92 meters.
  • ⚖️ The force acting on the particle is determined by the negative slope of the potential energy curve, which is evaluated between 1.9 meters and 4 meters to be a positive 4.3 Newtons.
  • 📉 The potential energy curve shows a decrease in potential energy as the particle moves from x = 6.5 meters towards the turning point, indicating work done by the particle against the force.
  • 📚 The script emphasizes the importance of understanding the relationship between kinetic and potential energy, as well as how to calculate them from a given potential energy curve.
  • 🤔 The problem-solving approach in the script involves using the conservation of mechanical energy principle and geometric methods to find unknown quantities such as velocity and turning points.
  • 🔧 The script provides a step-by-step guide to solving the problem, from identifying the total mechanical energy to calculating the particle's speed and locating the turning point.
Q & A

  • What is the mass of the particle in the problem?

    -The mass of the particle is 2 kilograms.

  • At what position does the particle have a velocity of -4 meters per second?

    -The particle has a velocity of -4 meters per second at x = 6.5 meters.

  • How is the total mechanical energy of the particle calculated?

    -The total mechanical energy is calculated using the kinetic energy formula: E_total = (1/2)mv^2. With a mass of 2 kg and a velocity of 4 m/s, the total energy is 16 joules.

  • What is the particle's speed at x = 4.5 meters?

    -The particle's speed at x = 4.5 meters is 3 meters per second.

  • How do you determine the kinetic energy at a specific point on the potential energy curve?

    -The kinetic energy at a specific point is determined by subtracting the potential energy at that point from the total mechanical energy.

  • What is the potential energy at x = 4.5 meters?

    -The potential energy at x = 4.5 meters is 7 joules.

  • How is the particle's turning point calculated?

    -The particle's turning point is calculated using the concept of similar triangles on the potential energy graph and solving for x using the proportions of the triangles.

  • What is the x-coordinate of the particle's turning point?

    -The x-coordinate of the particle's turning point is approximately 1.92 meters.

  • How is the force acting on the particle in a given region determined from the potential energy curve?

    -The force acting on the particle is determined by taking the negative slope of the potential energy curve over the specified region.

  • What is the force acting on the particle in the region from 1.9 meters to 4 meters?

    -The force acting on the particle in the region from 1.9 meters to 4 meters is 4.3 newtons.

Outlines
00:00
📚 Introduction to Potential Energy Curves

This paragraph introduces a physics problem involving potential energy curves. A 2-kilogram particle moves along an x-axis under the influence of a conservative force. The potential energy is plotted in a graph, and the particle's velocity at a specific point is given. The task is to determine the particle's speed at x=4.5 meters, locate its turning point, and evaluate the force acting on it within a certain region. The total mechanical energy is calculated using the given velocity and mass at x=6.5 meters, revealing that all energy is kinetic at this point, which simplifies the calculation.

05:01
🔍 Calculating Particle Speed and Locating Turning Point

The second paragraph delves into the calculation of the particle's speed at x=4.5 meters using the total mechanical energy previously determined and the potential energy at that point. The kinetic energy is found by subtracting the potential energy from the total energy, leading to the calculation of the velocity. The turning point of the particle is then located by using geometric similarity between two triangles on the potential energy graph, employing the concept of similar triangles to find the x-coordinate where the potential energy is zero, indicating the turning point at 1.92 meters.

📉 Evaluating the Force Acting on the Particle

The final paragraph addresses the calculation of the force acting on the particle within the region of 1.9 meters to 4 meters. It explains that the force can be determined from the slope of the potential energy curve, which is the negative of the slope since force is the negative derivative of potential energy. The slope is calculated using the change in potential energy and the change in position within the specified region, resulting in a positive force of 4.3 newtons, indicating the force's magnitude and direction.

Mindmap
Keywords
💡Potential Energy Curves
Potential energy curves are graphical representations that show the potential energy of a system as a function of position. In the video, this concept is central to understanding the behavior of a particle under the influence of a conservative force. The curve is used to determine the total mechanical energy of the system and to analyze the particle's motion.
💡Conservative Force
A conservative force is one that does not dissipate energy and whose work done on a particle is path-independent, relying only on the initial and final positions. In the context of the video, the conservative force acts along the x-axis and influences the potential energy of the particle, which is essential for calculating the particle's kinetic energy and total mechanical energy.
💡Mechanical Energy
Mechanical energy is the sum of kinetic and potential energy in a system. The video discusses how, at a certain position (x=6.5 meters), the particle's potential energy is zero, and all the mechanical energy is kinetic. This concept is crucial for determining the total energy of the system and for solving subsequent problems related to the particle's motion.
💡Kinetic Energy
Kinetic energy is the energy that a particle possesses due to its motion, defined as one-half the product of the particle's mass and the square of its velocity. In the video, the calculation of kinetic energy at x=6.5 meters is used to find the total mechanical energy of the particle, which is a key step in solving the problem.
💡Velocity
Velocity is a vector quantity that represents the rate of change of an object's position with respect to time. In the script, the particle's velocity at x=6.5 meters is given as negative four meters per second, indicating the speed and direction of the particle's motion, which is essential for calculating kinetic energy.
💡Turning Point
A turning point in the context of motion is a position where the direction of the particle's velocity changes. The video script discusses finding the turning point of the particle by using the potential energy curve and the concept of similar triangles, which is a critical step in understanding the particle's motion and energy changes.
💡Force
Force is the interaction that causes a change in the motion of an object. In the video, the force acting on the particle is related to the slope of the potential energy curve. The force is determined by the negative slope of the curve, indicating that a positive force is required to move the particle against the potential energy gradient.
💡Slope
Slope, in the context of a graph, is a measure of the steepness of a line and is calculated as the change in the vertical direction divided by the change in the horizontal direction. The video uses the slope of the potential energy curve to determine the force acting on the particle, with a negative slope indicating a restoring force.
💡Total Mechanical Energy
Total mechanical energy is the sum of all forms of energy in a mechanical system, including kinetic and potential energy. The video script emphasizes that at x=6.5 meters, the total mechanical energy is equal to the kinetic energy because the potential energy is zero, which is a key point in the analysis of the particle's motion.
💡Potential Energy
Potential energy is the stored energy of an object based on its position in a force field, such as gravitational or electric fields. In the video, potential energy is plotted against position to create a curve that helps determine the forces acting on the particle and its total mechanical energy at various positions along the x-axis.
💡Newton's Second Law
Although not explicitly mentioned in the script, Newton's Second Law (F = ma) is implicitly used when discussing forces and motion. The law relates the force acting on an object to its mass and acceleration. In the video, the force is calculated from the potential energy curve, which can be related to acceleration and, by extension, to Newton's Second Law.
Highlights

Introduction to potential energy curves and their significance in one-dimensional motion.

Explanation of how to determine the particle's speed using the total mechanical energy.

Calculation of the total mechanical energy with given mass, velocity, and potential energy at a specific point.

Use of kinetic and potential energy relationship to find the particle's speed at x = 4.5 meters.

Graphical representation of potential energy and its relation to kinetic energy.

Determination of the particle's turning point using the concept of like triangles.

Method to find the turning point's location by comparing areas under the potential energy curve.

Calculation of the turning point's x-coordinate using the slope of the potential energy curve.

Explanation of how the slope of the potential energy curve relates to the force acting on the particle.

Evaluation of the force acting on the particle within the region of 1.9 meters to 4 meters.

Concept of force as the negative slope on a potential energy graph.

Practical application of force calculation in the given region using the rise over run method.

Final calculation of the force magnitude as 4.3 Newtons.

Emphasis on the importance of understanding the relationship between kinetic and potential energy in mechanical systems.

Demonstration of problem-solving techniques in classical mechanics.

Educational value of visualizing physics concepts through graphs and equations.

Summary of the problem-solving process for potential energy and force calculations.

Transcripts

Browse More Related Video

Potential Energy Curves

Video 8.4: Potential Energy Graphs

Reading Potential Energy Graph

Potential Energy Curves

AP Physics C: Work, Energy, and Power Review (Mechanics)

AP Physics Workbook 4.O Conservation of Energy and Circular Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Potential EnergyConservative Force1D MotionKinetic EnergyMechanical EnergyParticle DynamicsTurning PointForce CalculationPhysics TutorialEnergy Graph