Potential Energy Curves
TLDRThis script delves into the concept of potential energy curves, illustrating how they represent the potential energy of a system as a function of position. It explains the relationship between the slope of the curve and the force acting on a particle, emphasizing that the negative slope corresponds to the force. The script further discusses how to derive kinetic energy from potential energy graphs by using the conservation of mechanical energy, highlighting the significance of turning points and equilibrium points in understanding particle motion.
Takeaways
- 📈 A potential energy curve is a graphical representation of potential energy (U) as a function of position (x) for a system under a conservative force.
- 🔄 The change in potential energy is equivalent to the negative work done on an object, which can be expressed as the integral of force over displacement.
- ↕ The slope of the potential energy curve at any point is related to the force acting on the particle, with the negative slope indicating the force.
- 🔄 By taking the derivative of the potential energy function with respect to position, the negative force can be determined.
- 📊 The force graph can be derived from the potential energy graph, with the force being the negative of the slope at any given point.
- 🔄 Kinetic energy can be found from the potential energy graph by using the conservation of mechanical energy, which is the sum of potential and kinetic energy.
- 🚫 Kinetic energy cannot be negative, and thus the point where the mechanical energy equals the potential energy is a turning point, beyond which the particle cannot move.
- 🔄 Equilibrium points are determined by the total mechanical energy and can be neutral, unstable, or stable, depending on the potential energy curve's shape and the total energy.
- 💡 At a neutral equilibrium, the system's mechanical energy equals its potential energy, and no force acts on the particle, as seen in a flat region of the potential energy curve.
- ⚠️ An unstable equilibrium occurs when a slight displacement results in a non-zero force that can cause the particle to move away, as in a potential energy curve's peak.
- 🛑 A stable equilibrium is where the particle is trapped between two turning points, unable to move in either direction without violating the conservation of energy.
Q & A
What is a potential energy curve?
-A potential energy curve is a plot of the potential energy (U) for a system as a function of position. It represents how the potential energy of a particle changes with its position in one-dimensional motion under the influence of a conservative force.
What is the relationship between potential energy and position?
-The potential energy is a function of position, and its change with respect to position is equal to the negative work done on the object. This relationship is depicted on the potential energy curve with the y-axis representing potential energy and the x-axis representing position.
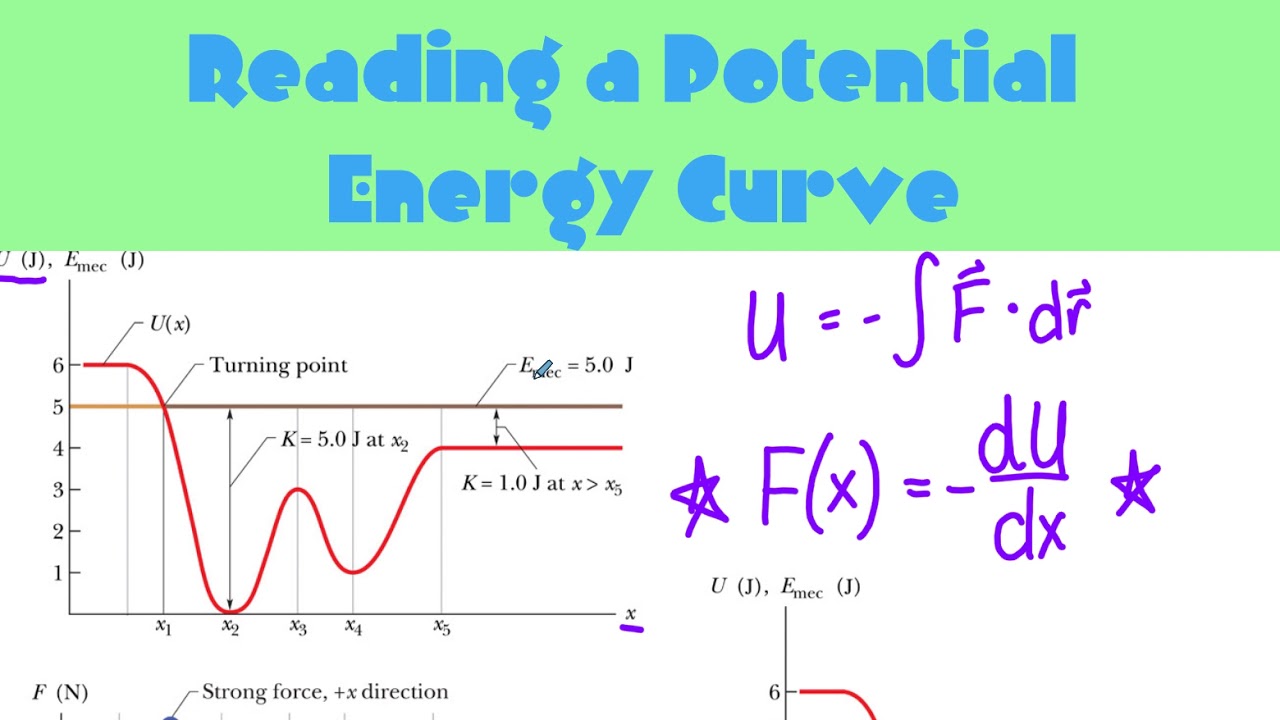
How is the slope of a potential energy curve related to force?
-The slope of the potential energy curve at any point is equal to the negative force acting on the particle at that position. Mathematically, this is expressed as \( \frac{dU}{dx} = -force \).
What does the negative slope on a potential energy curve indicate?
-A negative slope on the potential energy curve indicates a positive force acting on the particle, as the force is the negative of the slope of the curve.
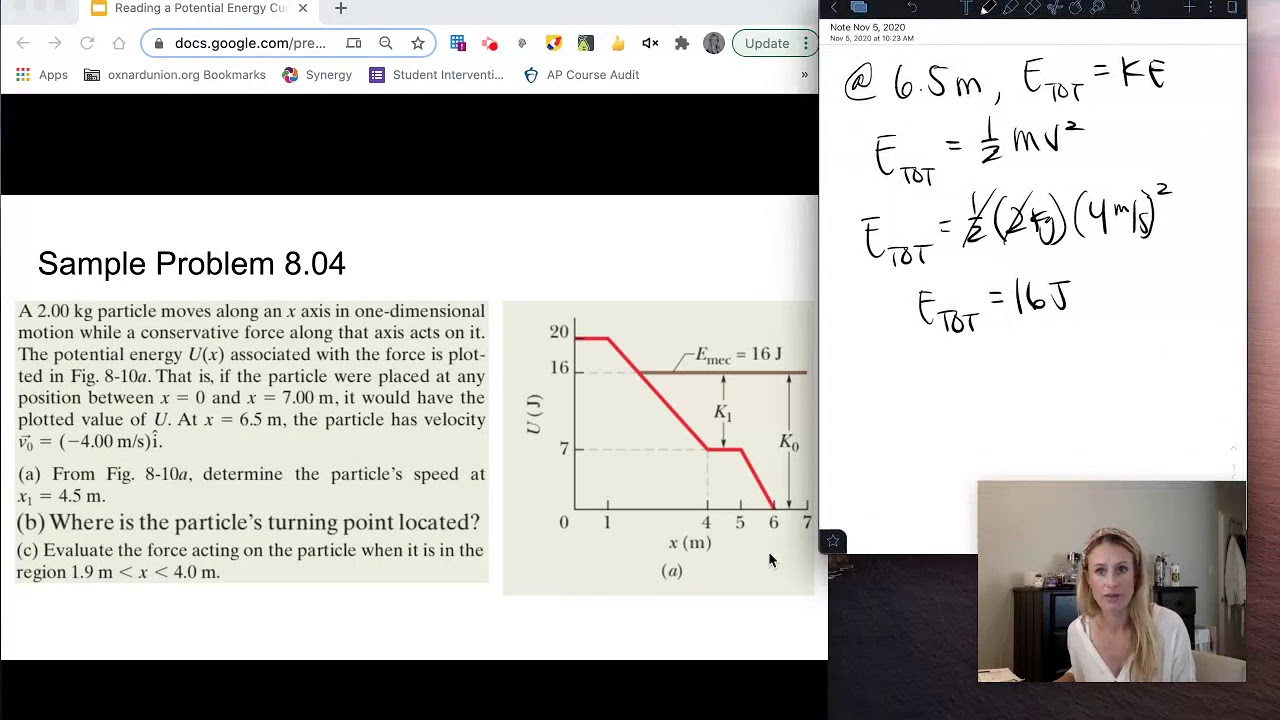
How can you determine the kinetic energy from a potential energy curve?
-Kinetic energy can be determined from a potential energy curve by knowing the total mechanical energy of the system, which is constant due to conservation of energy. Kinetic energy is calculated as the total mechanical energy minus the potential energy at a given position.
What is the significance of the horizontal line on a potential energy curve?
-The horizontal line on a potential energy curve represents the total mechanical energy of the system. It is used to find the kinetic energy at different positions by subtracting the potential energy from this constant value.
What are turning points on a potential energy curve?
-Turning points on a potential energy curve are positions where the particle cannot move beyond due to the kinetic energy becoming zero. These points are where the total mechanical energy line meets the potential energy curve.
What is an equilibrium point in the context of potential energy curves?
-An equilibrium point is a position on the potential energy curve where the net force acting on the particle is zero, and the particle is in a state of balance or rest.
What are the different types of equilibrium points mentioned in the script?
-The script mentions three types of equilibrium points: neutral equilibrium, unstable equilibrium, and stable equilibrium. Each type represents different conditions for the particle's motion and the forces acting on it.
Can kinetic energy ever be negative?
-No, kinetic energy cannot be negative because it is defined as \( \frac{1}{2}mv^2 \), where mass (m) is always positive, and velocity squared (v^2) is also always positive, even if the velocity itself is negative.
What is a potential well in the context of potential energy curves?
-A potential well is a region on the potential energy curve where a particle is confined between two turning points. The particle can move within this region but cannot escape due to the constraints of the total mechanical energy.
Outlines
📈 Understanding Potential Energy Graphs and Deriving Force
This paragraph explains the concept of a potential energy curve, which is a graphical representation of potential energy (u) as a function of position for a system under the influence of a conservative force. The y-axis represents potential energy, while the x-axis represents position. The slope of the curve at any point indicates the force acting on the particle, with the negative slope being equal to the force itself. The derivative of the potential energy function with respect to position yields the negative force. The paragraph also discusses how to interpret the slope to understand the force acting on a particle at various positions and how to derive a force graph from the potential energy graph.
🔄 Relating Potential Energy to Kinetic Energy and Mechanical Energy Conservation
The second paragraph delves into the relationship between potential energy, kinetic energy, and the conservation of mechanical energy in a system without non-conservative forces. It explains that mechanical energy is constant and can be represented by a horizontal line on the potential energy graph. The kinetic energy can be found by subtracting the potential energy from the total mechanical energy. The paragraph provides examples of how to use given information, such as the particle's release from rest or its kinetic energy at a certain position, to draw horizontal lines representing the total mechanical energy and subsequently determine the kinetic energy. It also introduces the concept of turning points, which are positions where the particle cannot move beyond due to the kinetic energy becoming zero, indicating a stop in motion.
⚖️ Types of Equilibrium Points in Potential Energy Graphs
The final paragraph discusses equilibrium points in the context of potential energy graphs. It differentiates between neutral, unstable, and stable equilibrium points based on the total mechanical energy and the characteristics of the potential energy curve. A neutral equilibrium occurs when the total mechanical energy equals the potential energy and no force acts on the particle, exemplified by a marble on a tabletop. An unstable equilibrium is when a slight displacement results in a non-zero force pushing the particle in that direction, like a marble on a rounded surface. A stable equilibrium is where the particle is stuck and cannot move in either direction without requiring negative kinetic energy, akin to a marble in a bowl. The paragraph also mentions the concept of a potential well, where a particle is confined within certain limits due to turning points.
Mindmap
Keywords
💡Potential Energy Curve
💡Conservative Force
💡Slope
💡Work-Energy Theorem
💡Derivative
💡Mechanical Energy
💡Kinetic Energy
💡Turning Point
💡Equilibrium Points
💡Neutral Equilibrium
💡Unstable Equilibrium
💡Stable Equilibrium
💡Potential Well
Highlights
Potential energy curves represent the potential energy U of a system as a function of position.
Potential energy changes with the position of a particle under a conservative force in one-dimensional motion.
The slope of the potential energy curve is related to the force acting on the particle, with negative slope indicating force.
The change in potential energy is equal to the negative work done on the object, derived from force times displacement.
Deriving force from potential energy involves taking the derivative with respect to position and applying a negative sign.
Graphical representation of force from a potential energy graph involves analyzing the slope at various positions.
At points of zero slope on the potential energy graph, the force acting on the particle is zero.
A negative slope on the potential energy graph corresponds to a positive force, and vice versa.
The total mechanical energy of a system is constant in the absence of non-conservative forces.
Kinetic energy can be determined from the potential energy graph by subtracting potential energy from total mechanical energy.
Turning points on the potential energy graph indicate positions where the particle cannot move beyond due to kinetic energy constraints.
Equilibrium points are identified by the relationship between total mechanical energy and potential energy at specific positions.
Neutral equilibrium occurs when the system's mechanical energy equals its potential energy, with no force acting on the particle.
Unstable equilibrium is characterized by a precarious balance where a slight displacement results in motion.
Stable equilibrium represents a position where the particle is stuck and cannot move in either direction without negative kinetic energy.
A potential well is a situation where the particle is confined within turning points, only able to move partway.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: