Reading Potential Energy Graph
TLDRThis video tutorial explains how to interpret a potential energy graph to understand the motion of a particle. It highlights the significance of mechanical energy, which remains constant and is the sum of kinetic and potential energy. The script discusses how to determine force and equilibrium points by taking derivatives and integrals of the potential energy function. It also explains how to identify turning points, where the particle must reverse direction due to insufficient mechanical energy, and how these points are calculated by setting the mechanical energy equal to the potential energy. The video encourages viewers to practice by answering questions about kinetic energy maxima and the physical implications of turning points.
Takeaways
- 📊 The video discusses how to interpret a potential energy graph to understand the motion of a particle.
- 🔄 The mechanical energy of an object, which includes kinetic and potential energy, remains constant regardless of position.
- 📚 Kinetic energy is calculated using the formula that relates it to the mass and the square of the velocity of the object.
- 📘 Potential energy is a function of position and can be different from the gravitational potential energy formula.
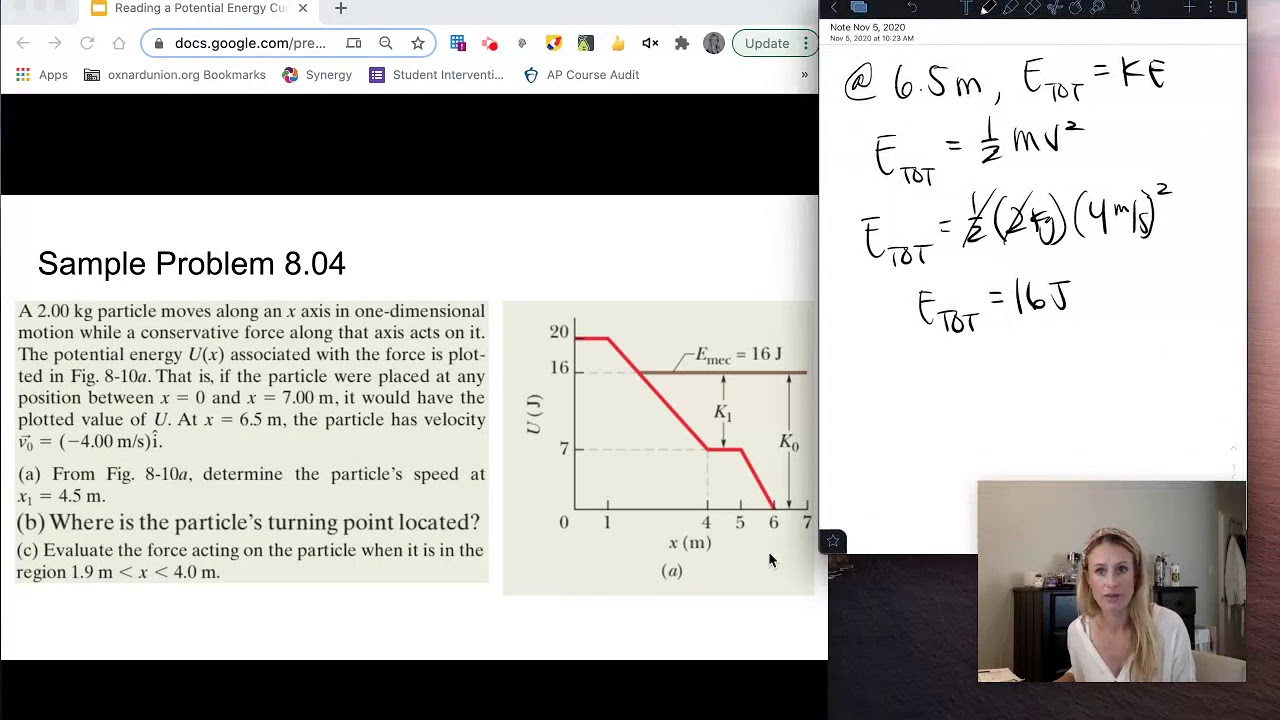
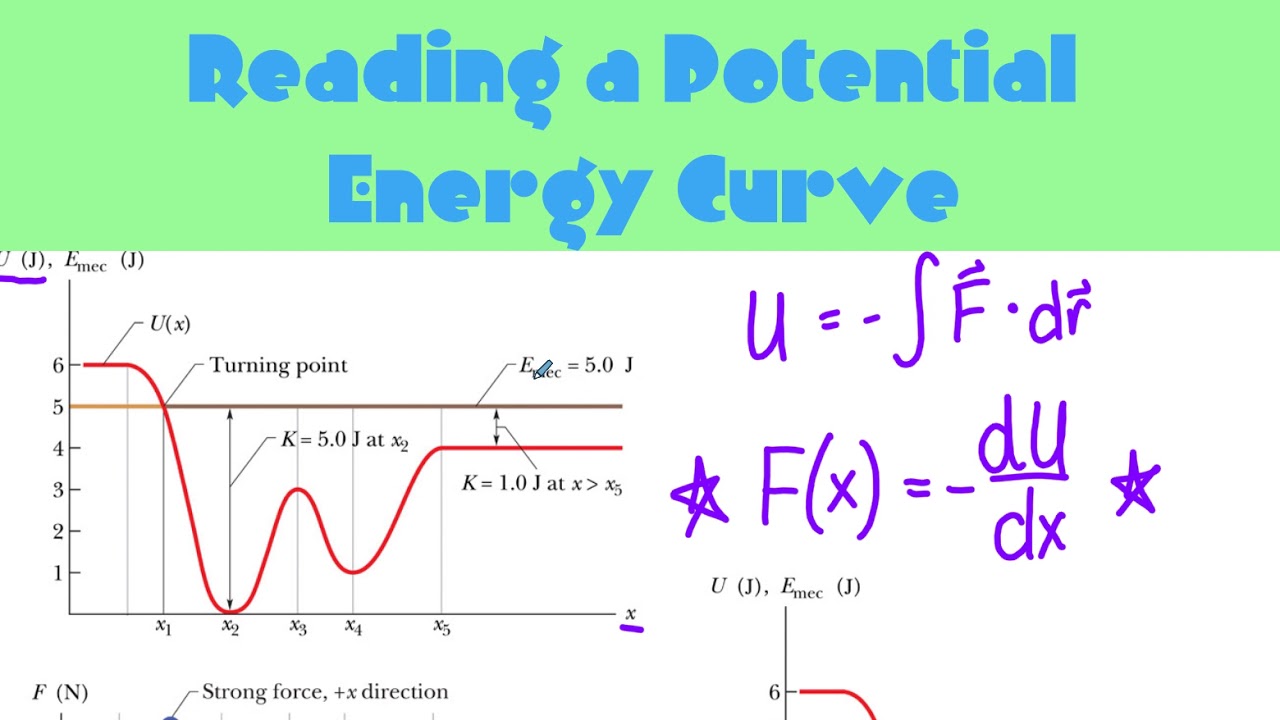
- 📍 Significant points on the graph, such as where the potential energy touches the x-axis, indicate zero potential energy.
- 🔄 Turning points on the graph represent positions where the total mechanical energy equals the potential energy, and the object would turn around.
- ⚖️ Equilibrium points occur where the derivative of the potential energy function is zero, indicating no net force acting on the particle.
- 🔻 Stable and unstable equilibrium points are differentiated by the direction in which a displaced particle will return to equilibrium.
- 🚫 The negative derivative of the potential energy function with respect to position gives the force acting on the particle, which should point against displacement for stability.
- 🔄 The sum of kinetic and potential energy at any point equals the mechanical energy, allowing us to determine kinetic energy from the graph.
- 🤔 The video poses questions to the viewer about where kinetic energy is greatest and what turning points physically define for the motion of the particle.
Q & A
What is the main idea of the video on reading a potential energy graph?
-The main idea of the video is to demonstrate how to extract information about the motion of a particle from a potential energy graph, which contains a wealth of information about the particle's kinetic and potential energy.
What is the significance of the purple line on the graph?
-The purple line on the graph represents the mechanical energy of the object at every given position, indicating that the mechanical energy remains constant regardless of the object's position.
How is mechanical energy defined in the context of this video?
-Mechanical energy is defined as the sum of kinetic energy and potential energy. It includes any energy that takes the form of motion or position.
What is the relationship between kinetic energy and the velocity of an object?
-Kinetic energy is directly proportional to the square of the velocity of the object. It can be calculated using the equation for kinetic energy with mass (m) and velocity (v).
How can potential energy be determined from the graph?
-Potential energy can be determined from the graph by looking at the function of potential energy as a function of position, which is represented by the blue line on the graph.
What are the equilibrium points on the graph and how are they identified?
-Equilibrium points are identified where the derivative of the potential energy function is equal to zero. These points occur where the force acting on the particle is zero, and they do not necessarily coincide with zero potential energy.
What is the difference between a stable and an unstable equilibrium point?
-A stable equilibrium point is where a displaced particle will return to its original position, while an unstable equilibrium point is where a slight displacement will cause the particle to move further away from the point towards a more stable position.
Why is the force acting on the particle negative when determining its equilibrium?
-The force is negative because it always points against the direction of displacement to maintain a stable equilibrium. If the force were positive, it would imply that the object is not returning to its stable equilibrium point.
How can one determine the kinetic energy at any point on the graph?
-The kinetic energy at any point can be determined by subtracting the potential energy at that point from the constant mechanical energy line. The difference represents the kinetic energy of the particle.
What does the turning point on the graph represent physically?
-The turning point represents the point at which the object would have to turn around and go back because it does not have enough total mechanical energy to exist beyond those points on the graph.
How can the position of a particle be restricted on the graph?
-The position of a particle can be restricted between certain points on the graph if the potential energy curve intersects the mechanical energy line at two points, indicating that the particle cannot escape the space between these two turning points.
Outlines
📈 Understanding Potential Energy Graphs
This paragraph introduces the concept of reading a potential energy graph to extract information about a particle's motion. The graph features the x-axis and two lines representing mechanical and potential energy. The mechanical energy remains constant regardless of position, defined as the sum of kinetic and potential energy. Kinetic energy is related to the square of the object's velocity, while potential energy is a function of position. Significant points on the graph, such as where the potential energy intersects the x-axis (zero potential energy) and the turning points where mechanical energy equals potential energy, are discussed. The force acting on the particle is the negative derivative of potential energy with respect to position, indicating equilibrium points where the force is zero.
🔍 Analyzing Forces and Turning Points
The second paragraph delves into the implications of the potential energy graph, explaining how forces can be determined by the negative derivative of potential energy. It discusses equilibrium points, distinguishing between stable and unstable ones, using the analogy of a marble in a valley. The force must be negative to ensure stability. The relationship between kinetic and potential energy is further explored, showing how they sum up to mechanical energy and allowing us to determine kinetic energy at any point on the graph. Turning points are defined as positions where the object must reverse direction due to insufficient mechanical energy to proceed further. The concept is applied to scenarios where potential energy curves intersect the mechanical energy line, indicating confined motion within certain positions. Practice questions are suggested to reinforce understanding, focusing on deriving force and making inferences about particle motion.
Mindmap
Keywords
💡Potential Energy Graph
💡Mechanical Energy
💡Kinetic Energy
💡Potential Energy Function
💡Turning Point
💡Conservative Force
💡Equilibrium Points
💡Stable Equilibrium
💡Unstable Equilibrium
💡Force Function
💡Practice Questions
Highlights
The video explains how to interpret a potential energy graph to understand the motion of a particle.
The graph contains the x-axis and a purple line representing the mechanical energy of an object at every position.
The blue line on the graph indicates the potential energy of the object as a function of its position.
Mechanical energy is conserved and remains constant regardless of position, defined as kinetic energy plus potential energy.
Kinetic energy is proportional to the square of the object's velocity, with the formula provided for calculation.
Potential energy can be any function of position, not limited to the gravitational potential energy equation.
Significant points on the graph, such as where the potential energy touches the x-axis, indicate zero potential energy.
The concept of a turning point is introduced, where the total mechanical energy crosses the potential energy curve.
Definitions of force acting on a particle are discussed, involving the negative derivative of potential energy with respect to position.
Equilibrium points are identified where the derivative of potential energy is zero, not necessarily at zero potential energy.
Stable and unstable equilibrium points are differentiated based on the particle's response to displacement.
The negative value of force is explained in the context of a valley, illustrating stable equilibrium.
The relationship between kinetic and potential energy is explored, showing how they sum up to mechanical energy.
The viewer is challenged to identify where the kinetic energy is greatest on the graph, hinting at the point of least potential energy.
The physical interpretation of the turning point is explained as the point where the object must reverse direction due to insufficient energy.
The concept of a particle being confined within certain positions due to insufficient mechanical energy is introduced.
The method to calculate turning points by setting mechanical energy equal to potential energy is described.
Practice questions are suggested for the viewer to apply the concepts of deriving force functions and making inferences about particle motion.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: