Video 8.4: Potential Energy Graphs
TLDRIn this educational video, the concept of potential energy curves is explored as a vital tool for physicists studying atomic structures. The script explains how potential energy is graphed against position, illustrating the force's effect on a particle at various locations. It introduces the relationship between potential energy change, work, and force, highlighting the importance of derivatives in determining force direction. The video also covers equilibrium points, distinguishing between neutral, stable, and unstable equilibria, and explains how to identify turning points based on kinetic and potential energy. The goal is to understand a particle's motion under different forces.
Takeaways
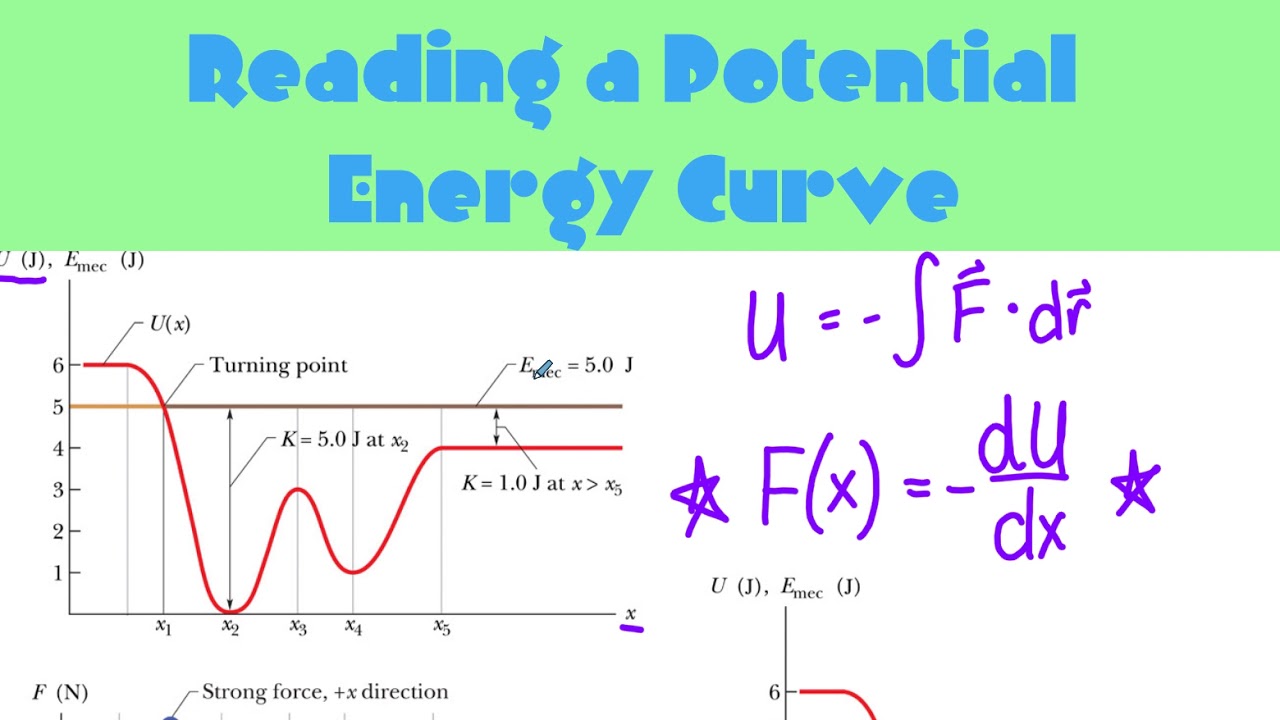
- 📈 The script introduces potential energy curves, which are graphs that show potential energy versus position for a particular force.
- 🔍 Potential energy curves are essential tools for physicists, especially when studying atomic structures.
- ⚖️ The change in potential energy (ΔU) is equal to the negative work done (W), which is the force (F) times the displacement (Δx).
- 📚 The force acting on a particle can be determined from the slope of the potential energy curve, with the force being the negative of the derivative of the graph.
- 📉 At points where the slope is negative, the force on the particle is positive, indicating the particle is pushed towards larger positions (downhill).
- 🔧 The concept of a turning point is explained, where the particle's kinetic energy equals a certain value, and the total energy determines the highest point it can reach.
- 🏁 Turning points are where the potential energy equals the total energy, and the kinetic energy is zero.
- 📌 Equilibrium points are identified where the net force is zero, indicated by a zero slope on the potential energy curve.
- 🔄 Equilibrium points can be neutral, stable, or unstable, depending on whether the particle remains in equilibrium, returns to a lower point, or moves further away when displaced.
- 📉 Neutral equilibrium occurs where the graph is flat for a large distance, stable equilibrium at local minima, and unstable equilibrium at local maxima.
- 🔮 The script encourages students to use potential energy graphs to identify equilibrium and turning points and to describe the qualitative motion of a particle under the influence of a force.
Q & A
What is a potential energy curve?
-A potential energy curve is a graph that represents the potential energy of a particle as a function of its position in relation to a particular force.
How is potential energy related to work done by a force?
-The change in potential energy is equal to the negative of the work done by the force, which can be expressed as ΔU = -W, where W = force times displacement (F * Δx).
What is the mathematical relationship between force and the derivative of potential energy?
-The force acting on a particle is the negative of the derivative of the potential energy with respect to displacement, expressed as F = -dU/dx.
How can you determine the direction of the force from the slope of the potential energy curve?
-If the slope of the potential energy curve is negative, it indicates that the force is positive, meaning the particle is pushed towards larger displacements (downhill).
What is a turning point in the context of potential energy curves?
-A turning point is a location on the potential energy curve where the kinetic energy of a particle is equal to the negative of the potential energy, and it represents the maximum height the particle can reach.
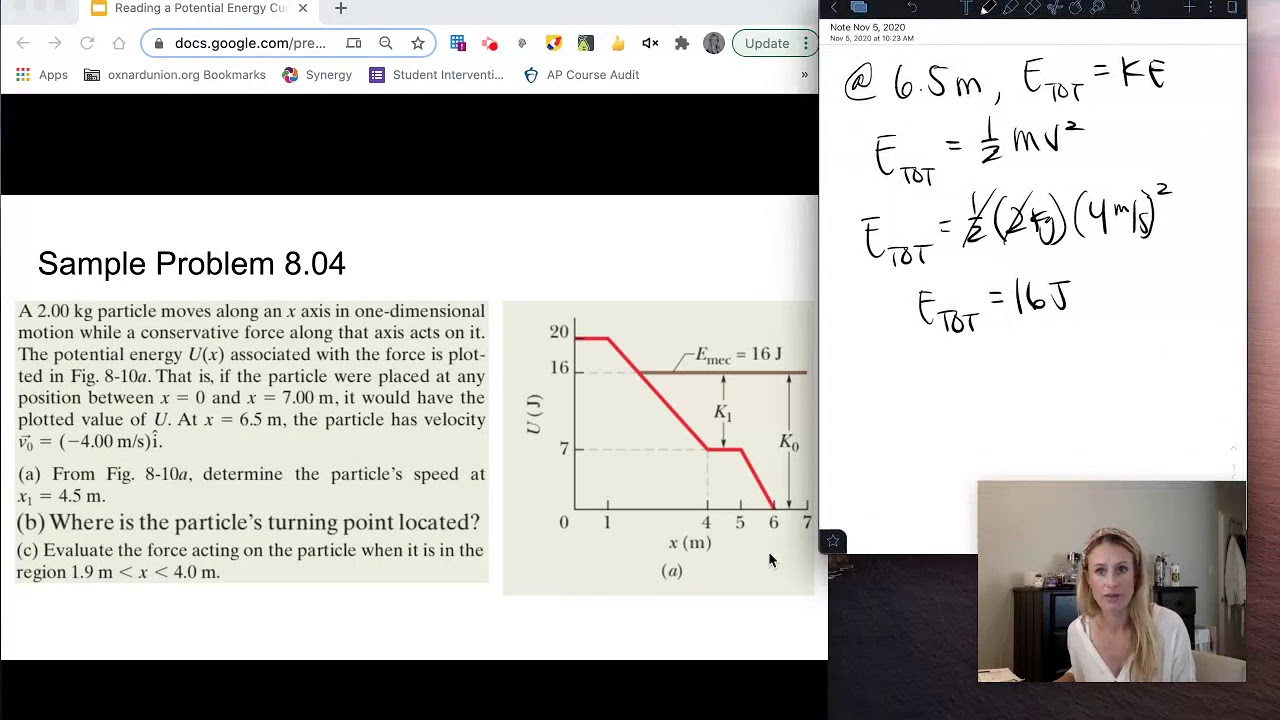
How can you calculate the total energy of a particle at a specific point on the potential energy curve?
-The total energy of a particle at a specific point is the sum of its kinetic and potential energies at that point.
What are equilibrium points on a potential energy curve?
-Equilibrium points are locations on the curve where the net force is zero, indicated by a zero slope on the potential energy curve.
What are the different types of equilibrium points?
-There are three types of equilibrium points: neutral equilibrium where the graph is flat for a large distance, stable equilibrium where the graph is a local minimum, and unstable equilibrium where the graph is a local maximum.
How can you determine if an equilibrium point is stable or unstable?
-An equilibrium point is stable if it is a local minimum (the particle tends to return to this point if displaced), and unstable if it is a local maximum (the particle will move away if displaced).
What is the significance of understanding turning points and equilibrium points in the study of atomic systems?
-Understanding turning points and equilibrium points helps in predicting the motion of particles under the influence of a force, which is crucial in studying atomic systems and their energy states.
What is the practical application of potential energy curves in physics?
-Potential energy curves are used by physicists as a primary tool for analyzing and understanding the behavior of particles in various systems, including atomic and molecular interactions.
Outlines
📈 Understanding Potential Energy Curves
This paragraph introduces the concept of potential energy curves, which are graphical representations of potential energy versus position. It explains that these curves illustrate the potential energy associated with a force at various positions of a particle. The paragraph also delves into the relationship between potential energy, work, and force, highlighting the equation delta U = -W and further breaking it down to show that force is the negative derivative of potential energy with respect to displacement. The concept of turning points is introduced, where the particle's kinetic energy equals the negative of its potential energy, indicating the maximum height it can reach. The paragraph concludes with an example of how to determine the total energy of a particle and the significance of turning points in its motion.
🔍 Analyzing Equilibrium and Turning Points
The second paragraph expands on the concepts of equilibrium points and turning points within the context of potential energy curves. It clarifies that equilibrium points are locations where the net force, and thus the slope of the potential energy curve, is zero. These points can be further classified into neutral, stable, and unstable equilibria based on the behavior of a particle when displaced. Neutral equilibrium occurs where the potential energy curve is flat, indicating no tendency for the particle to move. Stable equilibrium points are at local minima, where a displaced particle will return to the equilibrium position, while unstable equilibria are at local maxima, causing the particle to move further away upon displacement. The paragraph emphasizes the importance of identifying these points to predict and describe the qualitative motion of a particle under the influence of a force.
Mindmap
Keywords
💡Potential Energy
💡Potential Energy Curve
💡Work
💡Force
💡Derivative
💡Turning Point
💡Kinetic Energy
💡Equilibrium Point
💡Stable Equilibrium
💡Unstable Equilibrium
Highlights
Introduction to potential energy curves as a graph of potential energy versus position.
Potential energy curves are a primary tool for physicists studying atoms.
The relationship between potential energy change and work done by a force.
Derivation of force as the negative derivative of potential energy graph.
Explanation of how the slope of the graph indicates the direction of force on a particle.
Concept of turning points in potential energy curves where kinetic energy equals total energy.
Total energy calculation with given kinetic and potential energy values.
Turning points are where the particle cannot go higher due to total energy constraints.
Introduction of equilibrium points where net force and slope are zero.
Differentiation between types of equilibrium points: neutral, stable, and unstable.
Neutral equilibrium occurs where the graph is flat for a large distance.
Stable equilibrium is identified by local minima where displaced particles return to the low point.
Unstable equilibrium corresponds to local maxima where particles continue moving away after displacement.
Qualitative description of particle motion under the influence of potential energy forces.
Understanding how to identify equilibrium and turning points from potential energy graphs.
Practical application of the concepts in solving chapter 8 problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: