Potential Energy Curves

NunezPhysics
5 Oct 201705:37
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces potential energy curves, essential tools for analyzing an object's motion. It explains the relationship between force and potential energy, highlighting the use of derivatives to find force from potential energy graphs. The script emphasizes the importance of understanding equilibrium points, stable and unstable, and how the total mechanical energy line on the graph indicates an object's motion and energy distribution. Viewers are encouraged to practice analyzing potential energy curves through a textbook problem.

Takeaways
  • 📊 A potential energy curve is a graphical tool used to analyze an object's motion by plotting potential energy as a function of position.
  • ⚖️ The relationship between force and potential energy is given by the negative integral of force with respect to position, which can be reversed using a derivative.
  • 🔄 The derivative of potential energy with respect to position gives the force, which is crucial for understanding the slope of the potential energy curve.
  • 📉 The negative slope of the potential energy curve corresponds to the force acting on an object, providing insight into the object's motion.
  • 🚀 The total mechanical energy of an object is constant and is represented by a horizontal line on the potential energy curve, indicating the object's energy constraints.
  • 🚧 Areas above the total mechanical energy line are inaccessible to the object as it lacks the necessary energy to reach those positions.
  • 🔄 The sum of kinetic and potential energy equals the total mechanical energy, allowing us to determine the object's kinetic energy at different positions.
  • 🔄 Turning points on the potential energy curve indicate changes in the object's direction of motion, occurring where the curve intersects the total mechanical energy line.
  • ⚖️ Equilibrium points, which can be stable or unstable, are identified by maxima or minima on the potential energy curve, representing points where the object's motion could potentially stop.
  • 📚 The script instructs students to solve a problem involving potential energy curves for homework, emphasizing the importance of understanding these concepts for the AP test.
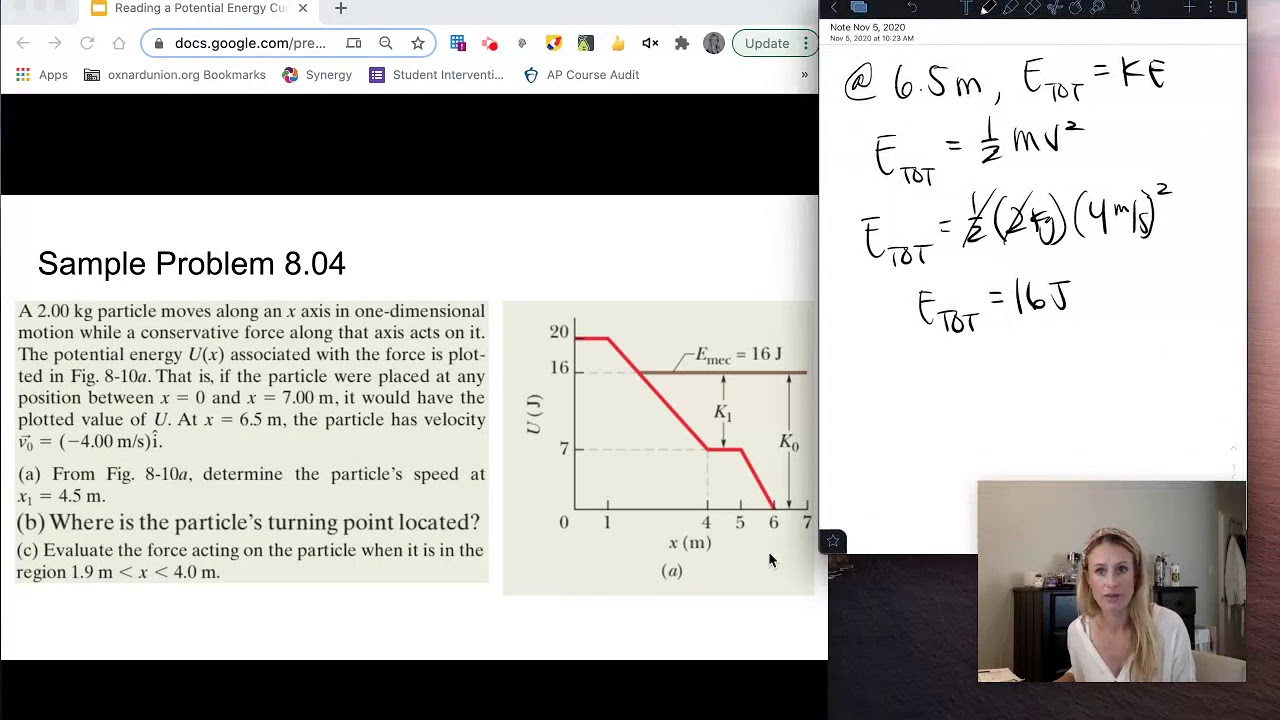
  • 📈 The script provides an example of how to interpret potential energy values at specific locations on the x-axis, encouraging students to practice analyzing potential energy curves.
Q & A

  • What is a potential energy curve used for?

    -A potential energy curve is used to analyze the motion of an object by graphing its potential energy as a function of its position.

  • What is the relationship between force and potential energy?

    -The potential energy of an object is equal to the negative integral of the force with respect to displacement. To find the force from potential energy, you take the negative derivative of the potential energy with respect to displacement.

  • How does the slope of a potential energy curve relate to force?

    -The negative slope of the potential energy curve corresponds to the force acting on the object. The steeper the slope, the greater the force.

  • What does the total mechanical energy line on a potential energy curve represent?

    -The total mechanical energy line represents the constant sum of kinetic and potential energy an object possesses, which it cannot gain or lose if all forces are conservative.

  • How can the total mechanical energy line help determine the possible positions of an object?

    -If a portion of the potential energy curve is above the total mechanical energy line, the object cannot reach positions to the left of that point because it does not have enough energy to do so.

  • What can be inferred about an object's kinetic energy from the potential energy curve?

    -At points where the potential energy is zero, all of the object's energy is kinetic. The difference between the total mechanical energy and potential energy at any point gives the kinetic energy.

  • What are equilibrium points on a potential energy curve?

    -Equilibrium points are locations on the potential energy curve where the object changes direction, typically where the curve intersects with the total mechanical energy line.

  • What is the difference between stable and unstable equilibrium points?

    -A stable equilibrium point, like a minimum on the curve, is where the object will return to if slightly displaced. An unstable equilibrium point, like a maximum, is where the object will move away from if displaced.

  • Why is it important to understand derivatives when analyzing potential energy curves?

    -Derivatives are important because they correspond to the slope of the graph, which in turn is equal to the force acting on the object, allowing you to analyze the object's motion.

  • What is an example of how to use the information from a potential energy curve?

    -By looking at the potential energy curve and the total mechanical energy line, you can determine the object's possible positions, its kinetic energy at different points, and the types of equilibrium points.

  • What homework problem is mentioned in the script, and what is its purpose?

    -Problem number 38 in the textbook is mentioned, which involves analyzing potential energy at certain locations on the x-axis. The purpose is to ensure understanding of potential energy curves by completing the problem and discussing it in class.

Outlines
00:00
📈 Understanding Potential Energy Curves

This paragraph introduces the concept of potential energy curves as a tool for analyzing the motion of an object. It explains how potential energy is graphed as a function of an object's position and the relationship between force and potential energy. The paragraph emphasizes the importance of understanding that the negative derivative of potential energy with respect to position gives the force, which is crucial for analyzing the graph's slope. It also discusses the significance of the total mechanical energy line on the graph, which indicates the object's maximum potential to do work. The paragraph further explains how the intersection of the potential energy curve and the total mechanical energy line can reveal information about the object's motion, including the points where it cannot reach due to insufficient energy and the points where all energy is kinetic. Additionally, it touches on equilibrium points, distinguishing between stable and unstable types based on the shape of the potential energy curve.

05:04
📚 Assignment on Potential Energy Curves

The second paragraph serves as an assignment prompt for students, directing them to problem number 38 in their textbook. This problem involves analyzing a given potential energy curve with specific values plotted on the x-axis in meters. The paragraph instructs students to complete the problem as homework, ensuring they understand the concept of potential energy curves. It also asks them to bring their work and answers to the next class meeting, reinforcing the importance of practicing and applying the knowledge gained from the video script.

Mindmap
Keywords
💡Potential Energy Curve
A potential energy curve is a graphical representation that shows the potential energy of an object as a function of its position. It is essential in analyzing the motion of an object, as it helps to visualize the energy changes with respect to position. In the video script, the potential energy curve is used to explain the relationship between force, potential energy, and the object's position, highlighting how the curve's slope corresponds to the force acting on the object.
💡Force
Force is a physical quantity that describes the interaction between two objects, causing a change in motion. In the context of the video, force is related to potential energy through the integral and derivative operations. The script mentions that the potential energy of an object is equal to the negative integral of force with respect to displacement, and conversely, force can be found by taking the derivative of potential energy with respect to position.
💡Derivative
The derivative in calculus is a measure of how a function changes as its input changes. In the video, the derivative is used to relate potential energy to force, stating that the negative derivative of potential energy with respect to position gives the force acting on an object. This concept is crucial for understanding how the slope of the potential energy curve represents the force at different positions.
💡Slope
Slope is a concept in mathematics that describes the steepness and direction of a line. In the video, the slope of the potential energy curve is directly related to the force acting on an object. A negative slope indicates that as the object moves in the direction of increasing position, the force does negative work, which corresponds to an increase in potential energy.
💡Total Mechanical Energy
Total mechanical energy is the sum of an object's kinetic and potential energies. The video script explains that this value is conserved in a closed system with conservative forces. The script uses the total mechanical energy line on the potential energy curve to illustrate the object's energy state and to determine the possible positions the object can occupy.
💡Conservative Forces
Conservative forces are forces in a system where the work done in moving a particle between two points is independent of the path taken. In the video, it is mentioned that if all forces acting on an object are conservative, the object cannot gain or lose energy, which is a fundamental concept in understanding the conservation of mechanical energy.
💡Kinetic Energy
Kinetic energy is the energy an object possesses due to its motion. The video script explains that at certain points on the potential energy curve, such as at x2 where the potential energy is zero, all of the object's energy is kinetic, indicating the object is moving with maximum speed at that position.
💡Equilibrium Points
Equilibrium points are positions in a system where the net force acting on an object is zero. The video distinguishes between stable and unstable equilibrium points based on the shape of the potential energy curve. A stable equilibrium, like at x2, is where the object tends to return to the equilibrium position if displaced, while an unstable equilibrium, like at x3, is where the object moves away from the position if disturbed.
💡Turning Point
A turning point on a potential energy curve is where the object changes direction, which corresponds to the point where the potential energy curve intersects with the total mechanical energy line. The video script uses this concept to explain that at a turning point, all the object's energy is potential, indicating the object is momentarily at rest.
💡Work
Work in physics is defined as the product of the force applied to an object and the displacement of the object in the direction of the force. The video script implies that work is done on an object to move it against a force, such as moving it to a position with higher potential energy to the left of x1, where it initially does not have enough energy to reach.
💡Potential Energy Values
Potential energy values are specific numerical values assigned to positions on the potential energy curve. The video script refers to a problem in a textbook that provides potential energy values at certain locations on the x-axis, which students are asked to analyze and graph to understand the object's energy state at different positions.
Highlights

A potential energy curve is a tool used to analyze the motion of an object by graphing potential energy as a function of the object's position.

The relationship between force and potential energy is given by the negative integral of force with respect to position.

To find the force from potential energy, take the negative derivative of potential energy with respect to position.

Derivatives correspond to the slope of a graph, allowing us to determine the force from a potential energy curve.

A straight line on a potential energy curve represents the total mechanical energy of an object, which is a constant value.

The total mechanical energy line helps determine the possible positions an object can occupy based on its energy.

An object cannot reach positions above its total mechanical energy line as it lacks the necessary energy.

Kinetic energy can be deduced from the potential energy curve by knowing the total mechanical energy.

At points where potential energy is zero, all the object's energy is kinetic.

A turning point on the potential energy curve indicates a change in the object's direction of motion.

Equilibrium points on the potential energy curve are identified by maximums and minimums.

A U-shaped minimum represents a stable equilibrium, where the object returns to the equilibrium point after a slight displacement.

An unstable equilibrium occurs at a maximum, where a slight displacement causes the object to move away from the equilibrium point.

Problem 38 in the textbook provides an example of analyzing potential energy at specific locations on the x-axis.

Understanding potential energy curves is crucial for solving problems related to the motion of objects.

Students are encouraged to complete problem 38 for homework to reinforce their understanding of potential energy curves.

Transcripts

Browse More Related Video

Video 8.4: Potential Energy Graphs

Potential Energy Curves

Potential Energy Graph Example

AP Physics 1 Energy Review

Reading Potential Energy Graph

Mr Chua, can you explain the F=-dU/dx formula?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Potential EnergyPhysics AnalysisEnergy GraphsForce DerivativesMechanical EnergyConservative ForcesStable EquilibriumUnstable EquilibriumKinetic EnergyEnergy ConservationPhysics Education