AP Physics Workbook 4.O Conservation of Energy and Circular Motion
TLDRThe video transcript discusses a physics problem involving the conservation of energy and circular motion. It delves into a scenario with a cart moving between spheres representing different planets, using the conservation of energy principle to calculate the cart's speed at a specific point. The analysis includes the impact of height differences and the radius of curvature on the cart's trajectory, ultimately providing equations to determine if the cart remains on the track or not. The problem-solving process is detailed, emphasizing the importance of understanding the principles of centripetal force and potential vs. kinetic energy.
Takeaways
- 📚 The tutorial is focused on Unit 4 of AP Physics Workbooks, specifically work and energy, and the conservation of energy in circular motion.
- 🔄 The scenario involves a cart moving from the top of a Jupiter sphere to the top of a Neptune sphere, highlighting the transformation of potential energy to kinetic energy and back.
- 📈 The conservation of energy principle is used to determine the speed of the cart when it is on top of the Neptune sphere, using the equation mg(2r) = mgh (where h = 2r) to find the velocity.
- 🚫 A mistake is corrected in the script where it's clarified that the kinetic energy at the top of Jupiter is zero, and the potential energy on Neptune is calculated by subtracting Neptune's potential energy from Jupiter's.
- 🌀 Centripetal acceleration is introduced as the acceleration towards the center of the circular motion, which is a key factor in the analysis of the cart's motion.
- 🔢 The final velocity equation derived is v = √(2g(r - r)), which shows the dependency of the cart's velocity on the height difference (r - r) between the two spheres.
- 🔽 The normal force on the cart at the top of the Neptune sphere is calculated, and it's determined that if the height difference (r - r) is too great, the cart will lose contact with the track due to the increased velocity.
- 🔄 The script discusses two perspectives from engineers regarding the cause of the cart losing contact with the track: one attributes it to the height difference, while the other points to the small radius of curvature of the track.
- 🌟 The tutorial emphasizes the importance of understanding the conservation of energy and centripetal force in solving problems related to circular motion and potential energy transformations.
- 📝 The mathematical analysis concludes that for the cart to stay on the track, the radius of the second planet (r) must be greater than or equal to one-fifth of Jupiter's radius, making Saturn the suitable choice.
- 🎓 The script serves as a comprehensive guide for students preparing for the AP Physics exam, providing a detailed walkthrough of a complex problem involving energy conservation and circular motion.
Q & A
What is the main concept discussed in the transcript?
-The main concept discussed in the transcript is the application of the conservation of energy principle to a physics problem involving a cart moving from one point to another, with a focus on circular motion and the factors affecting the cart's velocity and trajectory.
How does the height difference between Jupiter and Neptune affect the cart's velocity at point Q?
-The height difference between Jupiter and Neptune affects the cart's velocity at point Q by determining the potential energy that is converted into kinetic energy. A greater height difference (r minus r) results in a higher velocity due to the conservation of energy principle, where the potential energy at Jupiter is transformed into kinetic energy at Neptune.
What is the role of centripetal acceleration in the circular motion of the cart?
-Centripetal acceleration is responsible for keeping the cart moving in a circular path. It is directed towards the center of the circle and is necessary to change the direction of the velocity vector as the cart moves along the circular track.
How is the normal force related to the centripetal force in the context of the cart's motion?
-The normal force is the force exerted by the track on the cart, perpendicular to the surface. It is related to the centripetal force through the equation ma_c = mg - fn, where ma_c is the centripetal acceleration, mg is the gravitational force, and fn is the normal force. The balance between these forces determines whether the cart stays on the track or loses contact.
What happens if the radius of curvature of the track is too small?
-If the radius of curvature of the track is too small, the centripetal acceleration required for the cart to stay on the track becomes very high. This could result in the normal force not being sufficient to keep the cart on the track, causing it to lose contact and potentially fly off the track.
What is the significance of the conservation of energy principle in solving this problem?
-The conservation of energy principle is crucial in solving this problem as it allows us to relate the potential energy at one point to the kinetic energy at another point in the system. By applying this principle, we can calculate the cart's velocity at different points on the track and determine the conditions under which the cart remains on the track or not.
How does the mass of the cart affect the conservation of energy equation?
-The mass of the cart cancels out in the conservation of energy equation, indicating that the principle of conservation of energy does not depend on the mass of the objects involved. This simplifies the equation and allows us to focus on the relationship between potential and kinetic energies without considering the mass.
What is the relationship between the velocity of the cart and the radius of the circular track?
-The velocity of the cart is inversely related to the radius of the circular track. As the radius decreases, the required centripetal acceleration increases, which can lead to higher velocities for a given height difference, potentially causing the cart to lose contact with the track.
How does the height difference between the top of Jupiter and Neptune relate to the cart's trajectory?
-The height difference between the top of Jupiter and Neptune determines the potential energy that is converted into kinetic energy. A larger height difference results in a higher velocity at the top of Neptune, which can affect the cart's trajectory and whether it stays on the track or not.
What is the role of gravitational force in the conservation of energy calculations?
-The gravitational force plays a significant role in the conservation of energy calculations as it is the force that does work on the cart, converting potential energy into kinetic energy. The gravitational force is used to calculate the potential energy at different points and is essential for determining the cart's velocity and trajectory.
What conclusion can be drawn from the analysis of the cart's motion?
-The conclusion drawn from the analysis is that the cart's motion and its ability to stay on the track are influenced by the height difference between Jupiter and Neptune, the radius of curvature of the track, and the balance between gravitational force and normal force. Proper design of the track and understanding these physical principles are crucial for ensuring the cart's successful motion.
Outlines
📚 Introduction to Work and Energy Concepts
The paragraph introduces the topic of work and energy in the context of a physics workbook. It sets the stage for a discussion on the conservation of energy, particularly focusing on circular motion. The speaker aims to clarify the relationship between kinetic and potential energy as an object moves from one point to another, transforming its potential energy into kinetic energy. The paragraph also touches on the concept of centripetal acceleration and its role in maintaining circular motion, emphasizing the importance of velocity and force balance to prevent the object from flying out of the track.
🔄 Conservation of Energy in a Closed System
This paragraph delves into the application of the conservation of energy principle in a closed system, using the example of a cart moving between two spheres (Jupiter and Neptune). The speaker corrects a mistake from previous explanation, clarifying that the kinetic energy of Jupiter becomes zero and the potential energy (mgh) is equal to the potential energy on top of Neptune (mgh), with the height being 2r. The paragraph outlines the process of using the conservation of energy equation to solve for the speed of the cart when it is on top of the Neptune sphere, leading to the equation 0 = (mgh - mgh) + (1/2)mv^2, which simplifies to v = √(2gr).
🧮 Calculating Centripetal Force and Normal Force
The speaker continues the discussion by explaining the calculation of centripetal force and normal force in the scenario. The paragraph focuses on the equation ma = mg - fn, where a is the centripetal acceleration, and fn is the normal force. The speaker manipulates the equation to solve for fn, the normal force, and introduces the concept of velocity affecting the normal force due to the object's motion. The paragraph also explores the implications of a small radius of curvature on the track, as it goes over Neptune, and how it could cause the cart to lose contact with the track due to the extreme negative value it could reach.
🔧 Analyzing the Effects of Radius and Height Difference
In the final paragraph, the speaker analyzes the impact of the radius of the second planet (Neptune) and the height difference between Jupiter and Neptune on the cart's motion. The speaker uses the derived equations to discuss the conditions under which the cart would stay on the track, highlighting that the radius of the second planet must be greater than or equal to one-fifth of Jupiter's radius for the cart to maintain contact with the track. The speaker concludes by identifying Saturn as the suitable planet based on the calculations, providing a comprehensive understanding of the physical principles involved in the scenario.
Mindmap
Keywords
💡Conservation of Energy
💡Circular Motion
💡Kinetic Energy
💡Potential Energy
💡Centripetal Acceleration
💡Velocity
💡Force
💡Track
💡Cart
💡Height Difference
💡Normal Force
Highlights
The tutorial begins with an introduction to Unit 4: Work and Energy, focusing on the concepts of conservation of energy and circular motion.
A scenario is presented where an object moves from one point to another, transforming potential energy into kinetic energy, with a focus on circular motion and centripetal acceleration.
The importance of understanding the conservation of energy principle is emphasized, as it is crucial for solving the problem of the object's velocity at different points in its trajectory.
A mistake is corrected in the explanation, highlighting the need for precision and attention to detail when applying physical formulas and principles.
The concept of centripetal acceleration and its relationship with velocity and radius is discussed, with a clear explanation of how these factors interrelate in circular motion.
The tutorial delves into the calculation of the object's velocity at the top of the Neptune sphere, using the conservation of energy principle and the derived equations.
The significance of the height difference between the top of Jupiter and Neptune is analyzed, as it affects the object's velocity and its ability to stay on the track.
Engineer A's reasoning is examined, with a focus on the impact of the height difference on the object's velocity and the risk of it losing contact with the track.
Engineer B's alternative perspective is considered, emphasizing the role of the track's small radius of curvature in affecting the object's motion and the normal force.
A detailed mathematical analysis is provided to determine the conditions under which the object will stay on the track, based on the radius of the second planet.
The tutorial concludes with a comprehensive examination of the three possible scenarios for the object's motion on the second track, and the conditions for each.
The importance of understanding the relationship between gravitational force, centripetal force, and normal force is stressed for predicting the object's behavior.
The tutorial demonstrates the practical application of conservation of energy principles in physics problems, particularly in the context of circular motion and mechanical systems.
The problem-solving process is showcased, highlighting the iterative nature of refining and correcting equations to arrive at accurate solutions.
The tutorial emphasizes the value of a systematic approach to problem-solving, using step-by-step derivations and clear explanations to build understanding.
The discussion of potential real-world implications, such as the design of tracks for vehicles, underscores the relevance of the concepts covered in the tutorial.
The tutorial concludes with a clear and concise summary of the main points covered, reinforcing the key takeaways for the audience.
Transcripts
Browse More Related Video

'AP Physics 2023 Exam Solutions|Q1. PART C ( ii ) | Complete Step-by-Step Answers and Explanations"

Calculate Normal Force On a Roller Coaster Cart | Circular Motion
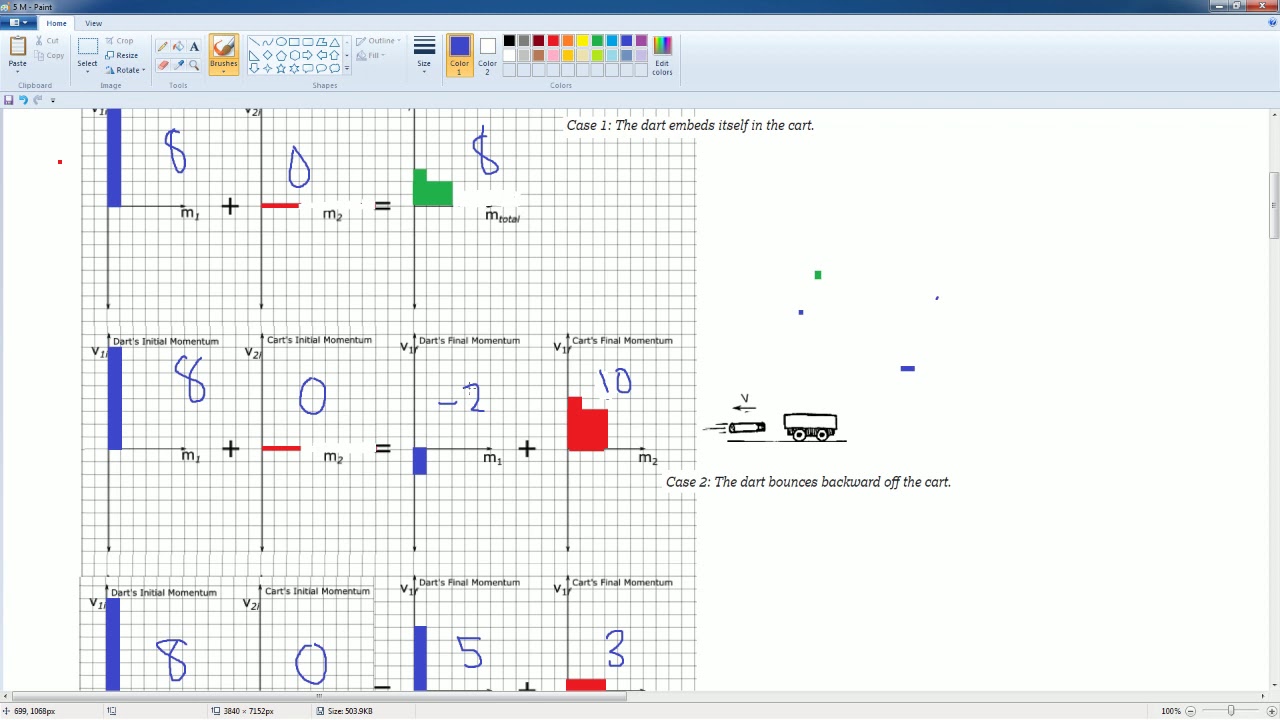
AP Physics Workbook 5.M Collisions
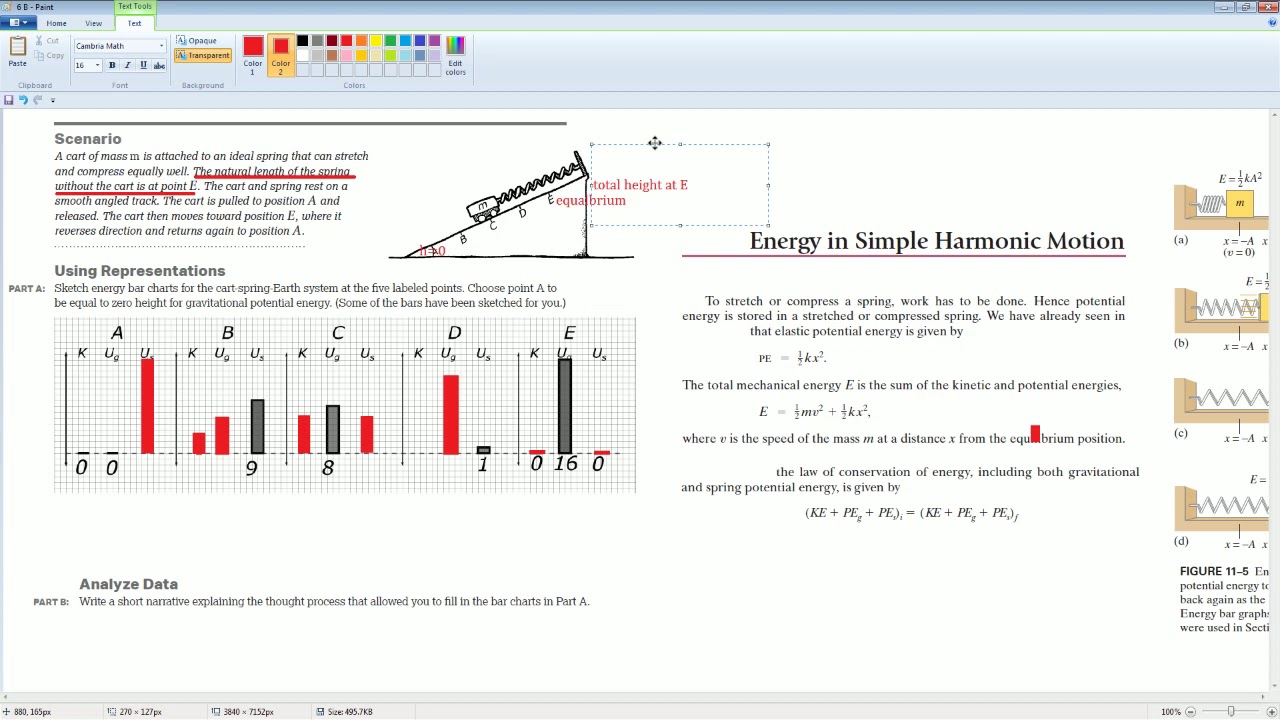
AP Physics Workbook 6.B Simple Harmonic Motion and Energy Review

AP Physics Workbook 6.A Forces in Simple Harmonic Motion
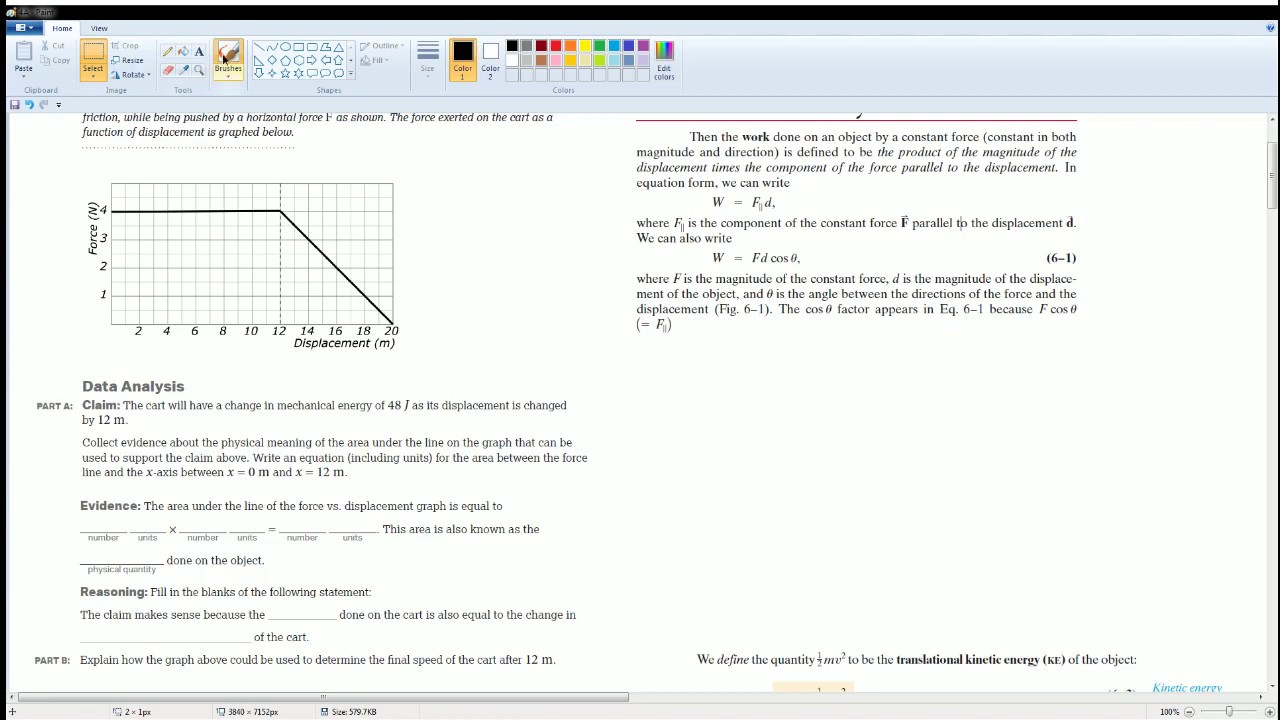
AP Physics Workbook 4.A Work
5.0 / 5 (0 votes)
Thanks for rating: