Angular motion variables | Moments, torque, and angular momentum | Physics | Khan Academy
TLDRThis instructional video demystifies rotational motion by explaining key concepts such as angular displacement, velocity, and acceleration. It uses the analogy of a tennis ball on a string to illustrate how these variables—measured in radians and represented by Greek letters (delta theta, omega, alpha)—describe an object's rotational movement. The video clarifies the difference between average and instantaneous values, emphasizing the convenience of angular variables in physics for analyzing rotational motion uniformly across a rigid object.
Takeaways
- 📚 Angular displacement (Δθ) is the angle through which an object rotates, measured in radians and is the change from initial to final angle (θ_final - θ_initial).
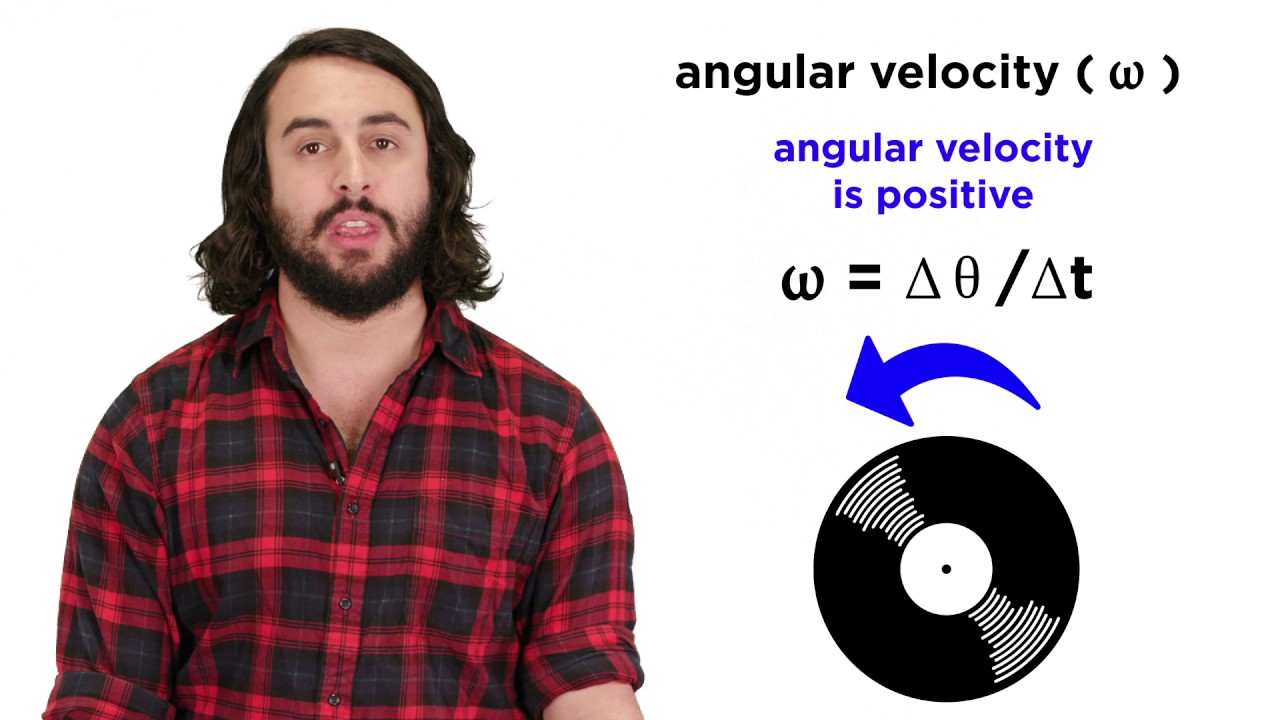
- 🔄 Angular velocity (ω) is the rate of rotation, analogous to linear velocity but measured in radians per second, and is represented by the Greek letter omega.
- 🚀 Angular acceleration (α) is the rate at which the angular velocity changes, measured in radians per second squared, and is represented by the Greek letter alpha.
- 🔄 Angular velocity is a vector quantity, indicating the direction of rotation, with counter-clockwise rotation considered positive and clockwise negative.
- 🔄 Angular acceleration is also a vector, pointing in the direction of the change in angular velocity, whether increasing or decreasing.
- 🔄 The concept of angular displacement is analogous to linear displacement (Δx), but for rotational motion.
- 📈 The average angular velocity is calculated as the total angular displacement divided by the time taken, which may not represent the instantaneous velocity at any given point.
- 📉 Angular acceleration can be found by taking the change in angular velocity over the change in time, and it indicates whether the object is speeding up or slowing down.
- 🎾 The example of a tennis ball on a string illustrates the concepts of angular displacement, velocity, and acceleration in a practical context.
- 🌐 Angular variables are particularly useful for describing the motion of rotating objects because they remain consistent across all points of a rigid object, unlike linear variables which vary with distance from the axis of rotation.
- 📐 Using radians instead of degrees for angular measurements is advantageous in rotational dynamics due to the direct relationship with the linear motion of points on a rotating object.
Q & A
What is the most basic quantity to describe the rotational motion of an object?
-The most basic quantity to describe the rotational motion of an object is angular displacement, symbolized by delta theta, which represents the change in angle the object has gone through.
How is angular displacement measured?
-Angular displacement is typically measured in radians, as opposed to degrees, for mathematical convenience in physics.
What is the relationship between angular displacement and regular displacement?
-Angular displacement is analogous to regular displacement, where regular displacement is the final position minus the initial position, denoted by delta x, and measured in meters.
What is angular velocity and how is it represented?
-Angular velocity is the rate at which an object changes its angle over time, analogous to regular velocity, and is represented by the Greek letter omega (ω).
What are the units of angular velocity?
-The units of angular velocity are radians per second, reflecting the rate of angular displacement over time.
How does the direction of rotation affect the sign of angular velocity?
-The direction of rotation affects the sign of angular velocity by considering counter-clockwise rotation as positive and clockwise rotation as negative.
What is angular acceleration and how is it defined?
-Angular acceleration is the rate at which the angular velocity of an object changes over time, defined as the change in angular velocity over the change in time.
What is the symbol used to represent angular acceleration?
-The Greek letter alpha (α) is used to represent angular acceleration.
How does angular acceleration relate to the change in an object's rotation speed?
-If an object's rotation speed is increasing, there is positive angular acceleration, and if the speed is decreasing, there is negative angular acceleration.
Why are angular variables more convenient for describing rotational motion than regular variables?
-Angular variables are more convenient because they allow for the description of motion for every point on a rotating object in a consistent manner, as all points on a rigid object have the same angular displacement, velocity, and acceleration.
What is the difference between average angular velocity and instantaneous angular velocity?
-Average angular velocity is the total angular displacement divided by the total time taken, while instantaneous angular velocity is the rate at which the object is rotating at a specific point in time.
How can you calculate angular acceleration if the initial and final angular velocities are known, along with the time taken?
-Angular acceleration can be calculated by taking the difference between the final and initial angular velocities and dividing by the time taken, represented as (omega_final - omega_initial) / time.
Outlines
📚 Introduction to Rotational Motion Variables
The instructor begins by addressing the complexity of tracking new rotational motion terms. The video aims to clarify concepts such as angular displacement, angular velocity, and angular acceleration. An example of a tennis ball rotating in a circle is used to illustrate these variables. Angular displacement, symbolized by delta theta, is defined as the change in angle, measured in radians for consistency with displacement in linear motion. The instructor explains that angular displacement is not necessarily zero after a full rotation and can accumulate for multiple revolutions.
🔄 Angular Velocity and Its Significance
The paragraph delves into angular velocity, denoted by the Greek letter omega, which is the rate of change of the angle over time, measured in radians per second. It is analogous to linear velocity but specific to rotational motion. The instructor uses the example of a tennis ball to explain that a higher angular velocity indicates a faster rotation rate. Angular velocity is also a vector, with direction determined by the right-hand rule, where counter-clockwise rotation is positive, and clockwise is negative.
⏱️ Angular Acceleration and Its Role in Rotational Dynamics
This section introduces angular acceleration, represented by the Greek letter alpha, which is the rate of change of angular velocity over time, with units of radians per second squared. The instructor explains that angular acceleration can either increase or decrease the angular velocity, depending on whether the object is speeding up or slowing down. If the angular velocity is constant, the angular acceleration is zero. The direction of angular acceleration is aligned with the change in angular velocity, either in the same direction for speeding up or opposite for slowing down.
📘 Practical Application of Angular Motion Variables
The instructor emphasizes the practicality of angular motion variables in describing rotational motion, especially for objects like a ball on a string. While linear motion variables vary with distance from the center of rotation, angular variables remain consistent across all points of a rigid object. This consistency simplifies the description of motion for all points on the object. The paragraph concludes with a sample problem involving a ball starting at rest and accelerating to a final angular velocity, allowing the calculation of angular displacement, average and instantaneous angular velocities, and angular acceleration.
Mindmap
Keywords
💡Rotational Motion
💡Angular Displacement
💡Radians
💡Angular Velocity
💡Omega (ω)
💡Linear Velocity
💡Angular Acceleration
💡Alpha (α)
💡Average Angular Velocity
💡Instantaneous Angular Velocity
💡Rigid Body
Highlights
Introduction to rotational motion variables such as angular displacement, angular velocity, and angular acceleration.
Explanation of angular displacement as the change in angle, symbolized by delta theta.
Angular displacement measured in radians for consistency with angular measurements.
Comparison of angular displacement to linear displacement, both measured from initial to final positions.
Introduction of angular velocity, defined as angular displacement over time, symbolized by omega.
Units of angular velocity are radians per second, differentiating it from linear velocity in meters per second.
Angular velocity as a vector quantity, indicating the direction of rotation with the right-hand rule.
Definition of angular acceleration as the rate of change of angular velocity over time, symbolized by alpha.
Units of angular acceleration are radians per second squared, indicating how quickly the rotation speed changes.
Angular acceleration as a vector, pointing in the direction of change in angular velocity.
Importance of angular variables for describing motion in rotating systems more conveniently than linear variables.
Illustration of how angular variables apply uniformly to all points on a rigid rotating object.
Example problem involving a tennis ball rotating in a circle to demonstrate calculation of angular variables.
Calculation of average angular velocity from rest to a given final velocity over a time period.
Distinguishing between average and instantaneous angular velocity and acceleration in the context of the example problem.
Concept that constant angular velocity implies zero angular acceleration, and vice versa for changing velocities.
Practical application of angular motion variables in solving rotational problems more efficiently.
Summary of key rotational motion variables and their significance in physics.
Transcripts
Browse More Related Video

College Physics 1: Lecture 23 - Rotational Motion
Angular Motion and Torque

AP Physics C: Rotational Kinematics Review (Mechanics)

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration

Relating angular and regular motion variables | Physics | Khan Academy

AP Physics 1 - Rotational Kinematics
5.0 / 5 (0 votes)
Thanks for rating: