Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration
TLDRThis video script offers a comprehensive introduction to rotational motion, covering key terms, definitions, and equations essential for understanding the subject. Starting with the concepts of arc length and angular displacement, the script explains how they relate to the radius and the angle theta in radians. It then delves into tangential and angular velocity, highlighting the difference between the two and how they are measured in meters per second and radians per second, respectively. The discussion continues with acceleration, differentiating between tangential and angular acceleration, and introducing the concept of centripetal acceleration, which acts towards the center of the circular path. The script also derives equations that connect these concepts, such as the relationship between arc length, angular displacement, and velocity. Furthermore, it explores the total acceleration of an object in circular motion using the Pythagorean theorem and trigonometric functions. Concluding with the relationship between frequency, period, and angular velocity, the script provides equations to calculate these quantities. The summary aims to equip viewers with a solid foundation in rotational motion to support their studies in physics.
Takeaways
- 📐 **Arc Length and Angular Displacement**: The arc length (s) is the distance an object travels along a circular path, measured in meters (m), while angular displacement (Δθ) is the change in angle in radians (rad).
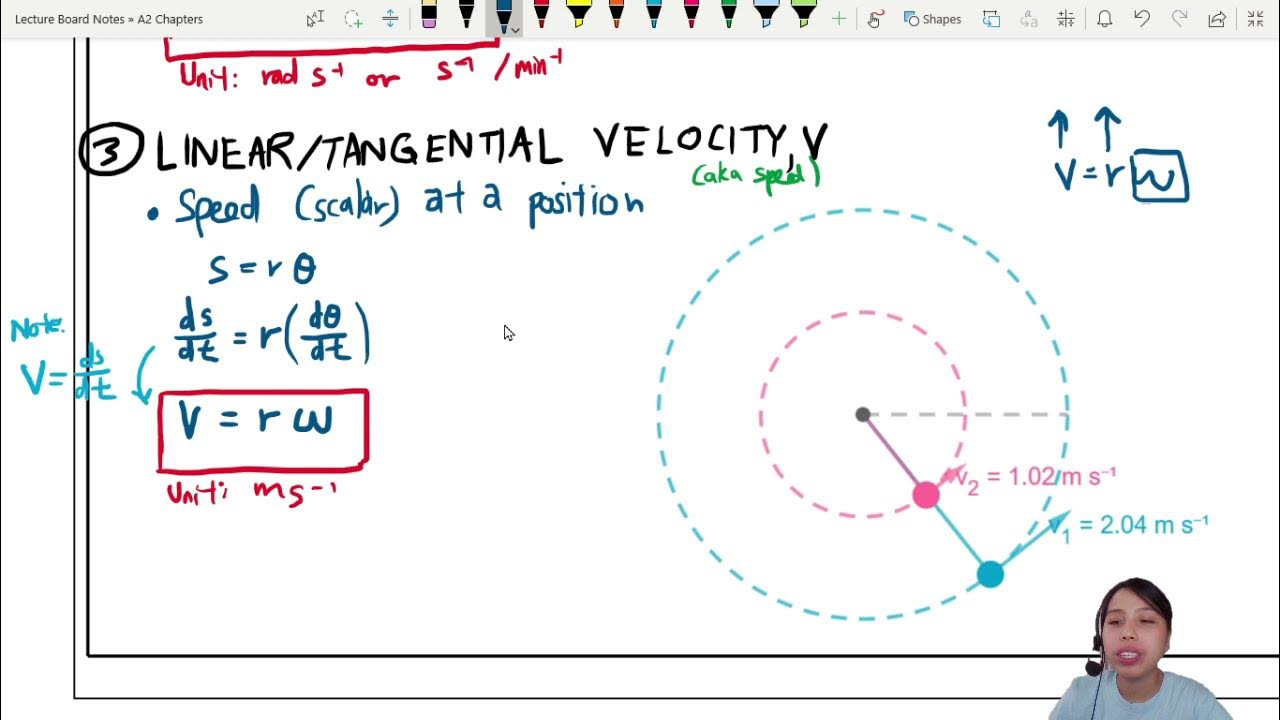
- 🌀 **Tangential and Angular Velocity**: Tangential velocity (v) is the speed of an object moving along the arc, measured in meters per second (m/s), and is tangent to the curve. Angular velocity (ω) is the rate of change of the angle over time, measured in radians per second (rad/s).
- 🔄 **Relationship Between Arc Length and Angular Displacement**: The arc length can be calculated by multiplying the radius (r) of the circle by the angular displacement in radians (s = r * θ).
- 🚀 **Velocity and Angular Velocity Connection**: The tangential velocity is directly proportional to the angular velocity (v = r * ω), indicating that velocity is dependent on the radius of the circle, while angular velocity is not.
- ⏱️ **Acceleration Types**: There are two types of acceleration in rotational motion - tangential acceleration (a_t), which is the change in tangential velocity over time, and angular acceleration (α), which is the change in angular velocity over time.
- 🔗 **Relating Tangential and Angular Acceleration**: Tangential acceleration is related to angular acceleration by the equation a_t = r * α, showing that acceleration along the tangent is a product of the radius and angular acceleration.
- 🎢 **Centripetal Acceleration**: This is the acceleration that acts towards the center of the circular path and is necessary for an object to follow a curved path. It is given by a_c = v^2 / r or a_c = r * ω^2.
- 🧮 **Total Acceleration Calculation**: The total acceleration of an object in circular motion is the vector sum of the tangential and centripetal accelerations, which can be found using the Pythagorean theorem (a_total = √(a_c^2 + a_t^2)).
- 📏 **Direction of Total Acceleration**: The direction of the total acceleration can be determined using the tangent function, relating the opposite (tangential) and adjacent (centripetal) components of the acceleration vector.
- ⏳ **Frequency and Period**: Frequency (f) is the number of cycles per second (Hz), and the period (T) is the time for one complete cycle. They are inversely related (f = 1/T and T = 1/f).
- 🔁 **Angular Velocity and Frequency/Period**: Angular velocity can be calculated from frequency (ω = 2 * π * f) or period (ω = 2 * π / T), which is useful for relating rotational speed to time measurements.
Q & A
What is the symbol used for arc length in the context of rotational motion?
-The symbol used for arc length is 's', which represents the distance an object moves along the circumference of a circle.
How is angular displacement represented in terms of the Greek alphabet?
-Angular displacement is represented by the Greek letter 'theta' (θ) and is used to measure the angle through which an object rotates.
What are the units used to measure arc length and angular displacement?
-Arc length is measured in meters (m), and angular displacement is measured in radians (rad).
How is tangential velocity defined in terms of arc length and time?
-Tangential velocity (v) is defined as the distance traveled along the arc length divided by the time taken to travel that distance, measured in meters per second (m/s).
What is the symbol for angular velocity and how is it related to the change in angle over time?
-The symbol for angular velocity is 'omega' (ω). It is defined as the change in the angle (Δθ) over the change in time (Δt), measured in radians per second (rad/s).
How does the size of the circle's radius affect the velocity of an object moving along its circumference?
-The size of the circle's radius directly affects the object's velocity. If the radius is larger, the object will cover a greater arc length in the same amount of time, resulting in a higher tangential velocity.
What is the relationship between the arc length and the angular displacement when the radius is constant?
-The relationship between arc length (s) and angular displacement (θ) is given by the equation s = r * θ, where r is the radius of the circle in meters and θ is the angular displacement in radians.
How is the tangential velocity related to angular velocity?
-The tangential velocity (v) is related to the angular velocity (ω) by the equation v = r * ω, where r is the radius of the circle.
What is the formula for centripetal acceleration and how is it derived?
-Centripetal acceleration (a_c) is given by the formula a_c = v^2 / r, where v is the tangential velocity and r is the radius of the circle. It is derived by considering the change in velocity of an object moving in a circular path and the fact that the acceleration vector points towards the center of the circle.
How can the total acceleration of an object in circular motion be calculated?
-The total acceleration (a_t) of an object in circular motion can be calculated using the Pythagorean theorem, with the equation a_t = √(a_c^2 + a_tan^2), where a_c is the centripetal acceleration and a_tan is the tangential acceleration.
What is the relationship between frequency and period in terms of rotational motion?
-Frequency (f) and period (T) are inversely proportional, with the relationship defined as f = 1/T. Frequency is the number of cycles per second, measured in Hertz (Hz), and the period is the time taken to complete one cycle, measured in seconds.
How can angular velocity be calculated if the frequency or period is known?
-If the frequency (f) is known, angular velocity (ω) can be calculated using the equation ω = 2πf. If the period (T) is known, ω can be calculated as ω = 2π/T.
Outlines
📚 Introduction to Rotational Motion Concepts
This paragraph introduces the fundamental concepts of rotational motion, including arc length (s), angular displacement (θ), tangential velocity (v), and angular velocity (ω). It explains how these terms relate to an object moving in a circular path, emphasizing the importance of measuring angles in radians and the role of the radius in determining arc length. The paragraph also differentiates between tangential velocity, which is the speed along the circular path, and angular velocity, which describes the rate of change of the angle over time.
🔗 Relationships Among Velocities and Accelerations
The second paragraph delves into the relationships between different types of velocities and accelerations in rotational motion. It discusses how tangential acceleration (a_t) is the change in tangential velocity over time, and angular acceleration (α) is the change in angular velocity over time. The paragraph also highlights the distinction between the velocities on different-sized circles and how angular velocity remains constant despite differences in radius. Furthermore, it derives equations that connect arc length to angular displacement, tangential velocity to angular velocity, and tangential acceleration to angular acceleration.
🚀 Centripetal Acceleration and Total Acceleration
This paragraph focuses on centripetal acceleration, which is the acceleration that keeps an object moving in a circular path. It derives the formula for centripetal acceleration using the relationship between tangential velocity and angular velocity. The paragraph also explains how to calculate the total acceleration of an object in circular motion by combining centripetal and tangential accelerations using the Pythagorean theorem. Additionally, it covers the concepts of frequency (f) and period (T), and how they relate to angular velocity (ω), providing formulas for calculating these quantities.
📝 Summary of Rotational Motion Equations
The final paragraph summarizes the key equations and concepts discussed in the video. It recaps the formulas for centripetal acceleration, tangential acceleration, the relationship between arc length and angular displacement, and the connection between speed and angular velocity. The paragraph emphasizes the importance of these equations for understanding and calculating various aspects of rotational motion, providing a comprehensive overview of the topic.
Mindmap
Keywords
💡Rotational Motion
💡Arc Length (s)
💡Angular Displacement (theta)
💡Tangential Velocity (v)
💡Angular Velocity (omega)
💡Acceleration
💡Centripetal Acceleration
💡Radius (r)
💡Frequency (f)
💡Period (T)
💡Pythagorean Theorem
💡Trigonometric Functions
Highlights
Introduction to rotational motion with terms, definitions, and equations essential for studies in this area.
Explanation of arc length 's' as the distance an object moves along a circular path.
Definition of angular displacement, denoted by the Greek letter theta (θ), measured in radians.
Differentiation between tangential velocity (v) and angular velocity (ω), with v measured in meters per second.
Angular velocity (ω) is the rate of change of the angle over time, measured in radians per second.
The relationship between arc length and angular displacement, where arc length equals radius times angular displacement in radians.
Derivation of the equation relating tangential velocity to angular velocity, with v = r * ω.
Explanation of how the size of the circle's radius affects tangential velocity but not angular velocity.
Introduction to tangential acceleration as the change in tangential velocity over time, measured in meters per second squared.
Angular acceleration (α) is the change in angular velocity over time, also measured in radians per second squared.
Derivation of the relationship between tangential acceleration and angular acceleration, with a = r * α.
Centripetal acceleration is the acceleration that keeps an object moving in a circular path, directed towards the center of the circle.
Equation for centripetal acceleration as a = r * ω^2, derived using the relationship between tangential velocity and angular velocity.
Total acceleration of an object in circular motion is the vector sum of centripetal and tangential accelerations, using Pythagorean theorem.
Calculation of the direction of total acceleration using the tangent function and the right triangle formed by centripetal and tangential accelerations.
Frequency (f) is the number of cycles per second, and the period is the time for one cycle; they are inversely related.
Angular velocity can be calculated from frequency using ω = 2πf or from the period using ω = 2π / T.
Summary of key equations and concepts for rotational motion, including arc length, angular displacement, velocities, accelerations, and the relationship between frequency and angular velocity.
Transcripts
Browse More Related Video

AP Physics C: Rotational Kinematics Review (Mechanics)

Relating angular and regular motion variables | Physics | Khan Academy
Circular Motion: Acceleration (Angular, Tangential, Centripetal)

Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration
12.1a Circular Motion Kinematics | A2 | Cambridge A Level 9702 Physics

angular velocity: what is it and how is it calculated
5.0 / 5 (0 votes)
Thanks for rating: