College Physics 1: Lecture 23 - Rotational Motion
TLDRIn this physics lecture, the concept of rotational motion is explored, focusing on objects rotating around a central axis. Key terms such as angular position, arc length, and radians are introduced, alongside angular velocity and acceleration. The lecture parallels linear motion with rotational motion, explaining how angular velocity (omega) relates to linear velocity (v) and how angular acceleration (alpha) is calculated. Examples, including a wind turbine blade and a drill's rotation, illustrate the application of these principles. The lecture concludes with end-of-lecture questions to reinforce the concepts covered, emphasizing the importance of understanding rotational motion in physics.
Takeaways
- 📚 The lecture introduces rotational motion, which is the movement of objects around a central axis, and compares it to linear motion discussed earlier in the course.
- 📐 To define angular position, one needs to know the radius (R) and the angle (Theta), measured counterclockwise from the positive x-axis, similar to how position is defined by an origin, distance, and direction.
- 🌐 Angular position is related to arc length (s) and radius (R) through the equation Theta = s/R, and the conversion between degrees and radians is established, with a full circle being 360 degrees or 2π radians.
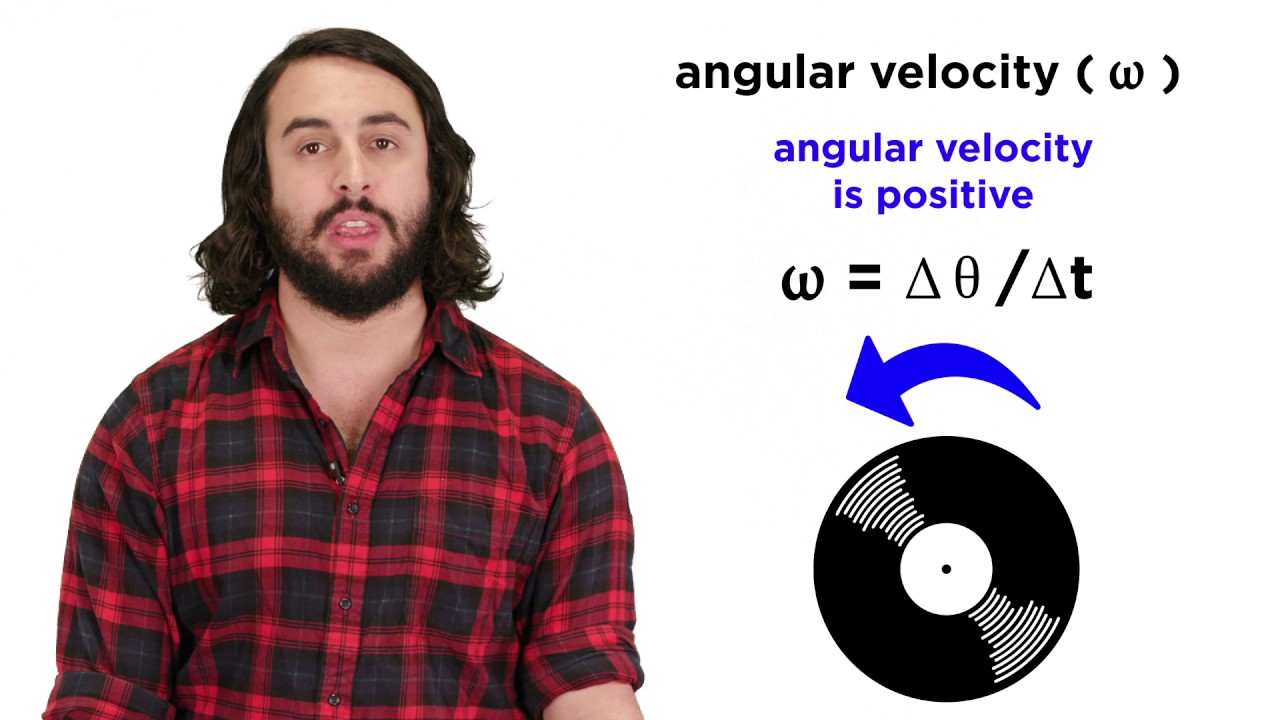
- 🔄 Angular velocity (ω) is the rotational equivalent of linear velocity (v), defined as the change in angular position over time (ΔΘ/ΔT), with units of radians per second.
- ⏱ The direction of rotation is important; counterclockwise rotation is positive, and clockwise rotation is negative for angular velocity.
- 🔗 The relationship between linear speed (v) and angular velocity (ω) is given by v = ωr, where r is the distance from the axis of rotation, showing that speed depends on both angular velocity and radius.
- 🌀 An example of a wind turbine blade is used to illustrate that all points on a rigidly rotating object share the same angular velocity, but points further from the center have greater linear speeds.
- 🛠 Angular acceleration (α) is defined as the rate of change of angular velocity over time (Δω/ΔT), with units of radians per second squared, and its direction depends on whether the object is speeding up or slowing down in its rotation.
- 🔗 The relationship between linear acceleration (a) and angular acceleration (α) is a = αr, highlighting that acceleration at a point depends on the angular acceleration and the radius.
- 🔧 The three key rotational motion equations analogous to the linear equations of motion are presented, though they are not frequently used in the course.
- 🛑 An example problem involving a drill rotating from rest to a certain speed is solved to demonstrate the calculation of angular acceleration and the number of revolutions made in a given time.
Q & A
What is rotational motion?
-Rotational motion refers to the movement of an object around a central axis. It is characterized by the object rotating and can be described using various quantities similar to linear motion, such as angular position, velocity, and acceleration.
How is angular position defined in rotational motion?
-Angular position in rotational motion is defined by both the radius (R) and the angle (Theta) through which the particle moves. It is measured counterclockwise from the zero-degree mark or the x-axis.
What is the relationship between arc length and angular position?
-The relationship between arc length (S) and angular position (Theta) is given by the equation where arc length is equal to the angular position multiplied by the radius (S = Theta * R).
Why do we use radians instead of degrees when discussing rotational motion?
-Radians are used instead of degrees in rotational motion because radians provide a more natural fit with the mathematical equations used to describe rotation. A full circle is 2π radians, which simplifies calculations involving the circumference of a circle and the angle swept out during rotation.
How is angular velocity related to linear velocity?
-Angular velocity (ω) is related to linear velocity (v) through the equation v = ω * r, where r is the distance from the central axis. This means that the linear speed of a point on a rotating object depends on both the angular velocity and the radius from the axis of rotation.
What is the difference between angular velocity and angular speed?
-Angular velocity is a vector quantity that includes both magnitude and direction of the rate of rotation, while angular speed is a scalar quantity that refers only to the magnitude of the angular velocity without considering direction.
How do you calculate the angular acceleration of an object?
-Angular acceleration (α) is calculated as the change in angular velocity (Δω) divided by the change in time (Δt), expressed by the equation α = Δω / Δt.
What is the relationship between angular acceleration and tangential acceleration?
-Tangential acceleration (a_t) is the acceleration experienced by an object moving in a circular path due to a change in its speed. It is related to angular acceleration (α) by the equation a_t = α * r, where r is the radius of the circular path.
How many revolutions does an object make when it has an angular velocity of 4π radians per second?
-An object with an angular velocity of 4π radians per second completes 2 revolutions per second, since one revolution is equivalent to 2π radians.
In the context of the lecture, why would Sophia have a greater speed than Rasheed on a merry-go-round?
-Sophia would have a greater speed than Rasheed on a merry-go-round if she is twice as far from the axis of rotation. According to the equation v = ω * r, if Sophia's radius (r) is twice that of Rasheed's, her linear speed (v) will also be twice as great, assuming they share the same angular velocity (ω).
Outlines
📚 Introduction to Rotational Motion
The lecture begins with an introduction to rotational motion, which involves objects rotating around a central axis. It parallels the concepts of position, velocity, and acceleration with their rotational counterparts. Angular position is defined as the angle through which a particle moves, measured counterclockwise from the positive x-axis. The relationship between arc length, radius, and angular position is established, leading to the introduction of radians as the unit for measuring angles in rotational motion. A conversion between radians and degrees is provided, highlighting that a full circle is 2π radians or 360 degrees.
🌀 Angular Velocity and Its Definitions
This section delves into angular velocity, which is analogous to linear velocity. Angular velocity (ω) is defined as the rate of change of angular position with respect to time. The importance of direction is emphasized, with counterclockwise rotation considered positive. The concept of period and frequency is introduced to define angular velocity in terms of a full circular path. The units of angular velocity are radians per second, and the relationship between linear velocity and angular velocity is established through the equation V = ωR, where V is the linear velocity, ω is the angular velocity, and R is the radius.
🌪️ Understanding Angular Acceleration
Angular acceleration is introduced as the rate of change of angular velocity over time, similar to how linear acceleration is the rate of change of linear velocity. The units of angular acceleration are radians per second squared. The direction of angular acceleration is discussed, with positive acceleration associated with counterclockwise acceleration or clockwise deceleration. The relationship between linear acceleration and angular acceleration is explored, with the tangential acceleration being equal to angular acceleration times the radius (a_t = αR).
🔧 Calculation of Angular and Linear Quantities
The lecture continues with an example problem involving a wind turbine blade to illustrate the calculation of angular and linear quantities. Given the blade's rotation speed in revolutions per minute, the problem requires converting this to angular velocity in radians per second. Using the relationship between angular velocity and linear velocity, the speed at different points along the blade is calculated, demonstrating that speed depends on the distance from the central axis.
⚙️ Radians, Revolutions, and Angular Motion
This section clarifies the concepts of radians and revolutions, emphasizing their importance in understanding angular motion. The distinction between angular speed (omega) and linear speed (velocity) is made, and the conversion between these units is discussed. The lecture also addresses the potential confusion between similar-sounding terms and the use of Greek symbols, encouraging practice to overcome these challenges.
🛠️ Equations of Motion for Rotational Systems
The lecture presents the three key equations of motion for rotational systems, which are analogous to those for linear motion but with angular variables. These equations relate angular position (Theta), angular speed (Omega), and angular acceleration (Alpha) to time. Although these equations are not frequently used in the course, understanding their structure is important for grasping the concepts of rotational motion.
🔄 Complex Example: Drill's Angular Acceleration
A complex example involving a drill rotating from rest to a high speed is presented to demonstrate the application of concepts learned. The drill's angular acceleration is calculated from its change in angular velocity over time. The example also determines the number of revolutions made by the drill during its acceleration phase, highlighting the multi-step problem-solving process in rotational motion.
🎢 End of Lecture Questions on Rotational Motion
The lecture concludes with a series of questions to reinforce the concepts of rotational motion. These questions cover the calculation of period from angular velocity, comparison of angular velocities and linear speeds in a rotating system, and determination of the signs of angular speed and acceleration for a slowing down fan blade. The questions aim to deepen the understanding of rotational motion and its various components.
Mindmap
Keywords
💡Rotational Motion
💡Angular Position
💡Arc Length
💡Radians
💡Angular Velocity
💡Period and Frequency
💡Tangential Speed
💡Angular Acceleration
💡Centripetal Acceleration
💡Equations of Motion
Highlights
Introduction to rotational motion, focusing on objects rotating about a central axis.
Defining angular position using radius R and angle Theta.
Angular position measured counterclockwise from the positive x-axis.
Relating arc length to angular position through the equation Theta = S/R.
Introducing radians as the unit of angular measurement in rotational motion.
Conversion between radians and degrees, with one radian being 57.3 degrees.
Defining angular velocity (omega) as the rate of change of angular position over time.
Units of angular velocity are radians per second.
Directionality of angular velocity: positive for counterclockwise rotation, negative for clockwise.
Relating angular velocity to period and frequency of rotation.
Equation V = Omega * R links linear speed to angular speed and radius.
Example of wind turbine blade illustrating the relationship between angular velocity and linear speed.
Calculating speed at different points on a rotating wind turbine blade.
Introduction to angular acceleration (Alpha) as the rate of change of angular velocity over time.
Units of angular acceleration are radians per second squared.
Directionality of angular acceleration: positive for counterclockwise acceleration or clockwise deceleration.
Relating linear acceleration to angular acceleration through the equation A = Alpha * R.
Equations of motion for rotational motion analogous to linear motion equations.
Example problem involving a drill rotating from rest to 40 revolutions per second.
Calculating angular acceleration and revolutions made by a drill in a given time.
End of lecture questions to reinforce concepts of rotational motion.
Transcripts
Browse More Related Video

Angular motion variables | Moments, torque, and angular momentum | Physics | Khan Academy
Angular Motion and Torque

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration

Relating angular and regular motion variables | Physics | Khan Academy

Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration

Rotational Motion: Crash Course Physics #11
5.0 / 5 (0 votes)
Thanks for rating: