Calculate Normal Force On a Roller Coaster Cart | Circular Motion

INTEGRAL PHYSICS
1 Dec 202103:55
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script discusses a physics problem involving a roller coaster car. The focus is on calculating two key aspects: the normal force between the cart and track at point A, and the maximum speed at point B to ensure the cart stays in contact with the track. The script explains the importance of considering both gravity and the normal force when analyzing centripetal force. Using the given mass, speed, and radius of curvature, the normal force at point A is calculated to be 9116 Newtons. For point B, the script outlines the conditions for the cart to just make it over the crest without losing contact, leading to a formula for the maximum speed. The explanation aims to clarify the concepts and calculations involved in such a physics scenario.

Takeaways
  • 🎢 The problem involves a roller coaster car coasting down a hill, passing through a trough, and ascending another hill.
  • 🔍 The first goal is to calculate the normal force between the cart and the track as it passes point A.
  • 📉 The second goal is to determine the maximum speed at which the cart can travel to ensure it remains in contact with the track.
  • 📚 A free body diagram is drawn to visualize the forces acting on the cart at point A, including the normal force and gravity.
  • 🚫 It's important to remember that the normal force cannot be directly equated to the centripetal force; the net force is what causes centripetal acceleration.
  • 📉 The net force is calculated by considering both the normal force and gravity, which together provide the centripetal force.
  • 🔢 Given values are used to solve for the normal force, with the car's mass being 250 kg, speed 20 m/s, and radius of curvature at point A being 15 meters.
  • 📌 The calculated normal force at point A is found to be 9116 Newtons.
  • 🔄 For point B, the objective is to find the maximum speed to prevent the cart from losing contact with the track.
  • 🌐 At the top of the hill, gravity continues to act on the cart, and the normal force becomes zero at the critical speed where the cart just barely stays in contact.
  • ⚖️ The mass of the cart is irrelevant in the calculation for the maximum speed at point B, as it cancels out in the equation.
  • 🏁 The maximum possible velocity is derived to ensure the cart does not 'jump' off the track, maintaining the roller coaster's functionality.
Q & A

  • What is the main objective of the roller coaster problem discussed in the script?

    -The main objective is to solve for two things: the normal force between the cart and the track as the cart passes point A, and the maximum speed at which the cart can travel at point B to ensure it remains in contact with the track.

  • What is a free body diagram and why is it important in this context?

    -A free body diagram is a graphical representation of all the forces acting on a body in a particular situation. It is important in this context to visualize and calculate the net force acting on the roller coaster cart, especially at points A and B.

  • Why can't we simply set the normal force equal to the centripetal force in this problem?

    -We can't do that because the centripetal force is the net force acting on the cart, which includes both the normal force and gravity. The net force is what causes the cart to accelerate centripetally.

  • What is the formula for centripetal force?

    -The formula for centripetal force is Fc = (mv^2)/r, where m is the mass of the object, v is the velocity, and r is the radius of curvature.

  • What is the calculated normal force at point A in Newtons, given the mass, velocity, and radius of curvature?

    -The calculated normal force at point A is 9116 Newtons, using the given values of mass (250 kg), velocity (20 m/s), and radius of curvature (15 meters).

  • What is the significance of the maximum speed at point B in the roller coaster scenario?

    -The maximum speed at point B is crucial because it determines the speed at which the cart can safely pass over the top of the hill without losing contact with the track and flying off.

  • Why is there no normal force acting on the cart at the very top of the hill (point B) when it's moving at the right speed?

    -At the very top of the hill, if the cart is moving at the right speed, it will momentarily be in free fall, meaning the only force acting on it is gravity, and there will be no normal force between the cart and the hill.

  • What happens if the cart goes over the top of the hill too slowly?

    -If the cart goes over the top too slowly, there will be a normal force acting upward on the cart, which is not desirable as it could lead to the cart losing contact with the track.

  • What happens if the cart goes over the top of the hill too fast?

    -If the cart goes over the top too fast, it will not stay in contact with the hill and will effectively become a jump, causing the cart to go off into space, which is not the desired outcome for a roller coaster.

  • How does the mass of the cart factor into the calculation for the maximum speed at point B?

    -The mass of the cart does not factor into the calculation for the maximum speed at point B. The equation for maximum speed at the top of the hill is independent of the cart's mass.

Outlines
00:00
🎢 Roller Coaster Physics: Normal Force and Maximum Speed

The video script discusses a physics problem involving a roller coaster car. It aims to calculate two key aspects: the normal force between the cart and the track at point A, and the maximum speed at point B to ensure the cart remains in contact with the track. The script begins by drawing a free body diagram for the cart at point A, where the normal force and gravity are considered to find the net centripetal force. Using the given values (mass of 250 kg, speed of 20 m/s, and radius of curvature of 15 m), the normal force at point A is calculated to be 9116 Newtons. Moving to point B, the script addresses the scenario where the cart is at the crest of a hill, and the goal is to find the speed that prevents the cart from losing contact with the track. The analysis involves considering the absence of normal force at the precise speed where gravity alone provides the centripetal force needed for circular motion. The script concludes by solving for this maximum velocity, ensuring the cart's successful traversal over the hill without becoming airborne.

Mindmap
Keywords
💡Roller Coaster
A roller coaster is a type of amusement ride that consists of a series of hills and valleys, where the cars move along a track. In the context of the video, the roller coaster car is the subject of the physics problem, where its motion and forces are analyzed as it travels down a hill, through a trough, and up another hill.
💡Normal Force
Normal force is the force exerted by a surface that supports the weight of an object resting on it, acting perpendicular to the surface. In the video, the normal force is a key factor in determining the pressure the roller coaster car exerts on the track, especially when solving for the force at point A.
💡Gravity
Gravity is the force that attracts two objects with mass towards each other, and in the context of Earth, it is the force that pulls objects downwards. In the video, gravity acts on the roller coaster car, influencing its motion and the forces it experiences, especially when calculating the normal force at point A and the maximum speed at point B.
💡Centripetal Force
Centripetal force is the net force that keeps an object moving in a circular path, directed towards the center of the circle. In the video, the centripetal force is crucial for understanding how the roller coaster car maintains its circular motion as it travels through the trough and over the hill.
💡Free Body Diagram
A free body diagram is a simplified illustration that shows all the forces acting on an object in a particular situation. In the video, the free body diagram is used to visualize and calculate the forces on the roller coaster car at points A and B, helping to solve for the normal force and maximum speed.
💡Mass
Mass is a measure of the amount of matter in an object, often related to its resistance to acceleration. In the script, the mass of the roller coaster car (250 kilograms) is used in the equations to calculate the normal force and the maximum speed it can travel without losing contact with the track.
💡Speed
Speed is a measure of how fast an object is moving, typically expressed in meters per second (m/s). In the video, the speed of the roller coaster car is a critical variable in determining the normal force it experiences and the maximum speed it can safely travel at point B.
💡Radius of Curvature
The radius of curvature refers to the radius of the circular path that an object follows. In the context of the video, the radius of curvature at point A (15 meters) is used to calculate the centripetal force required for the roller coaster car to navigate the curve.
💡Trough
In the context of roller coasters, a trough refers to the lowest point in the track where the car is at its lowest elevation before ascending another hill. In the video, the car passes through a trough, and the forces acting on it at this point are analyzed.
💡Crest
The crest is the highest point of a hill or curve on a roller coaster track. In the video, the roller coaster car must safely navigate over the crest at point B without losing contact with the track, which is where the concept of maximum speed becomes important.
Highlights

Problem setup involves a roller coaster car coasting down a hill, through a trough, and up another hill.

Objective is to solve for the normal force at point A and the maximum speed at point B to maintain contact with the track.

A free body diagram is drawn to analyze forces acting on the cart at point A.

Gravity and normal force are considered as the two forces acting on the cart.

Centripetal force is the net force causing the cart to accelerate centripetally.

Gravity force on the car is calculated and substituted into the net force equation.

The normal force at point A is found to be 9116 Newtons.

A free body diagram is also drawn for the cart at point B to find the maximum speed.

Gravity continues to act on the cart at point B, regardless of speed.

The normal force becomes zero at the correct speed where the cart is in free fall at point B.

The mass of the cart is irrelevant when calculating the maximum speed at point B.

The maximum possible velocity is calculated to prevent the cart from flying off the ramp.

The video provides a step-by-step approach to solving physics problems involving roller coaster dynamics.

The importance of considering both gravity and normal force in the analysis is emphasized.

Centripetal force is identified as the key to understanding the cart's motion.

The video concludes with a summary of the findings and a note of thanks to the viewers.

Transcripts

Browse More Related Video

AP Physics Workbook 3.E Maximum speed over the top

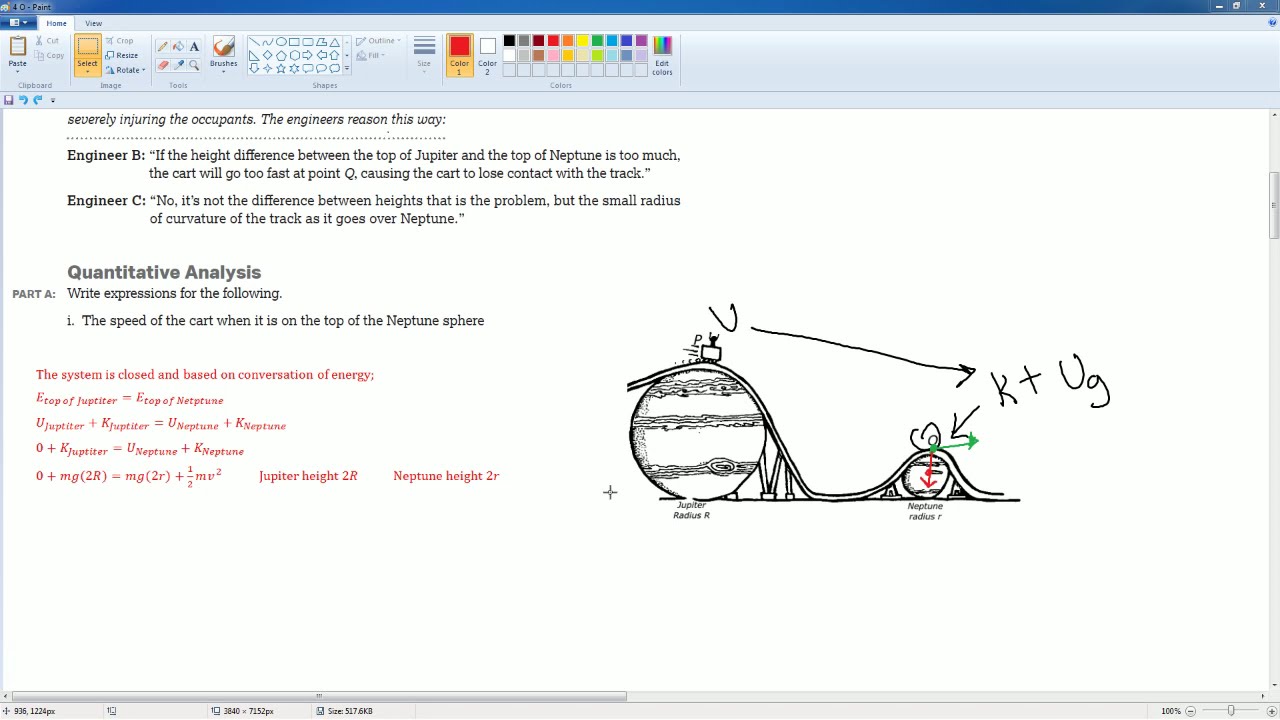
AP Physics Workbook 4.O Conservation of Energy and Circular Motion

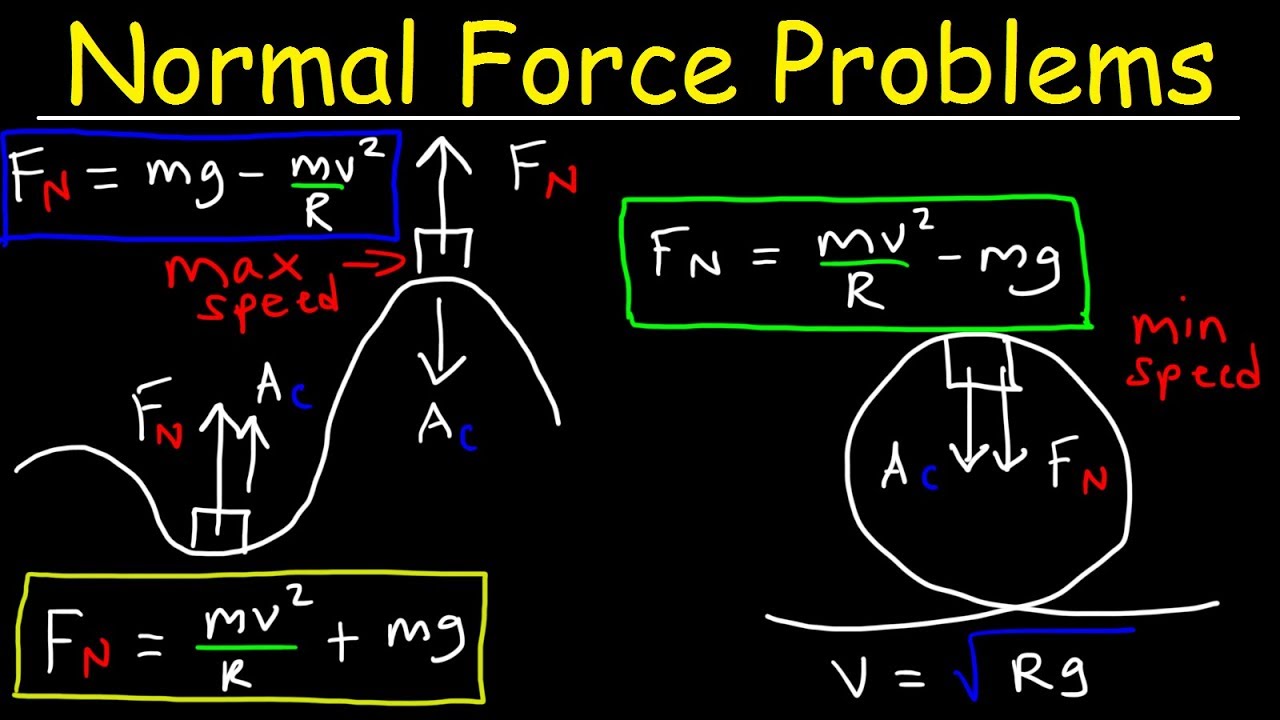
Normal Force on a Hill, Centripetal Force, Roller Coaster Problem, Vertical Circular Motion, Physics

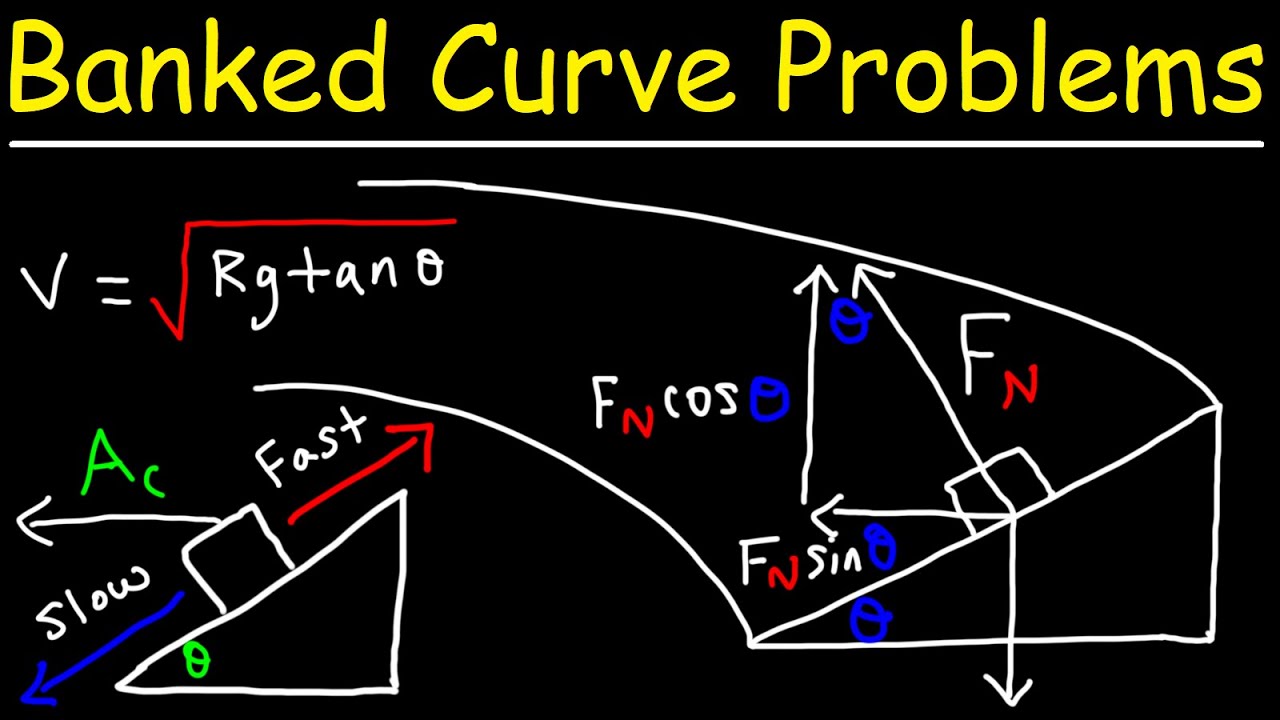
Banked turn Physics Problems

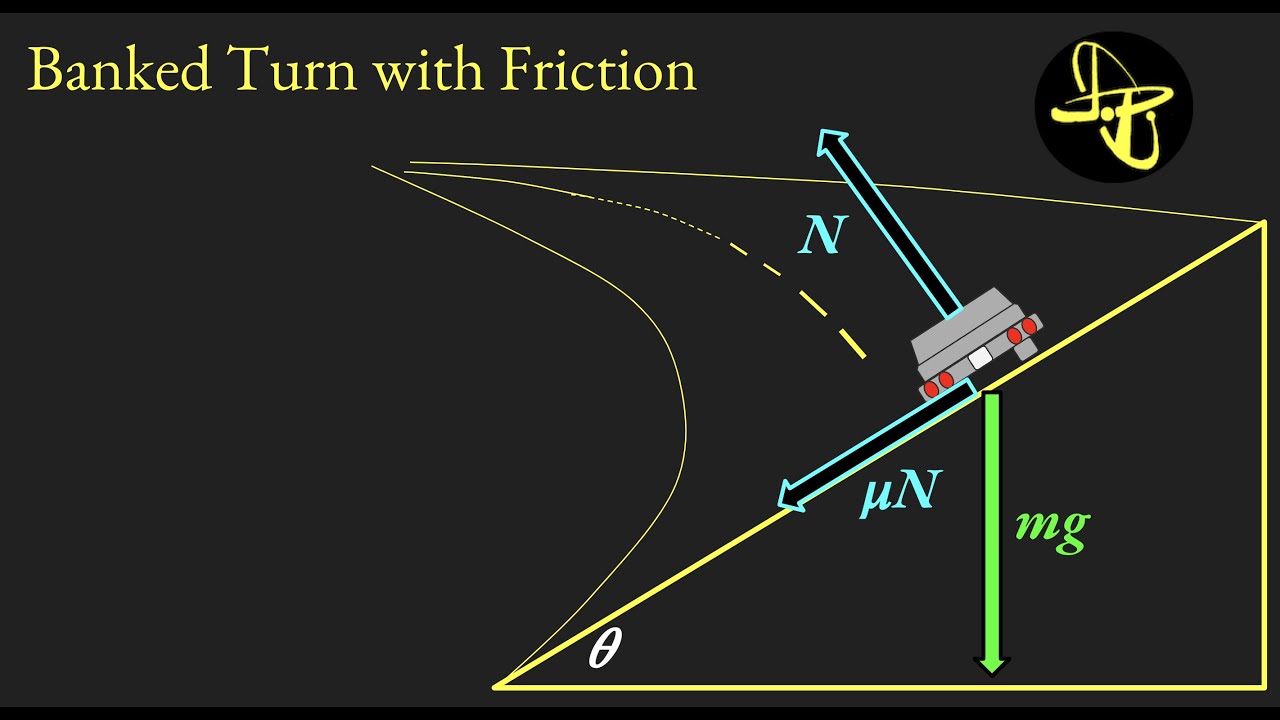
Banked Turn with Friction - Physics of Speed Limits on Banked Curves

Uniform Circular Motion - 3 - Ferris Wheel

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsRoller CoasterNormal ForceCentripetal ForceGravitySpeed CalculationFree Body DiagramMechanical EngineeringEducationalScience