Banked turn Physics Problems

The Organic Chemistry Tutor
15 Apr 202117:29
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script delves into the physics of banked curves, specifically addressing how a car can maintain equilibrium without friction on a banked curve. The script explains the difference between a regular incline and a banked curve, highlighting the unique forces at play, such as the normal force and centripetal force. It guides the viewer through the calculations needed to determine the speed at which a car can safely navigate a banked curve of a given radius and angle without sliding. The script also explores how altering the banking angle can affect the safe speed of a vehicle. The mathematical derivation leads to the formula for calculating the required speed and banking angle to prevent sliding, using principles of circular motion and trigonometry.

Takeaways
  • 🚗 The video focuses on the physics of banked curves and how they affect a car's motion.
  • 🎯 A car on a frictionless banked curve of radius 200 meters needs to travel at a specific speed to avoid sliding up or down the curve.
  • 📏 The banked curve is banked at an angle of 15 degrees, which is crucial for determining the required speed.
  • 🔍 The distinction between a banked curve and a regular incline is made clear, with the banked curve involving circular motion.
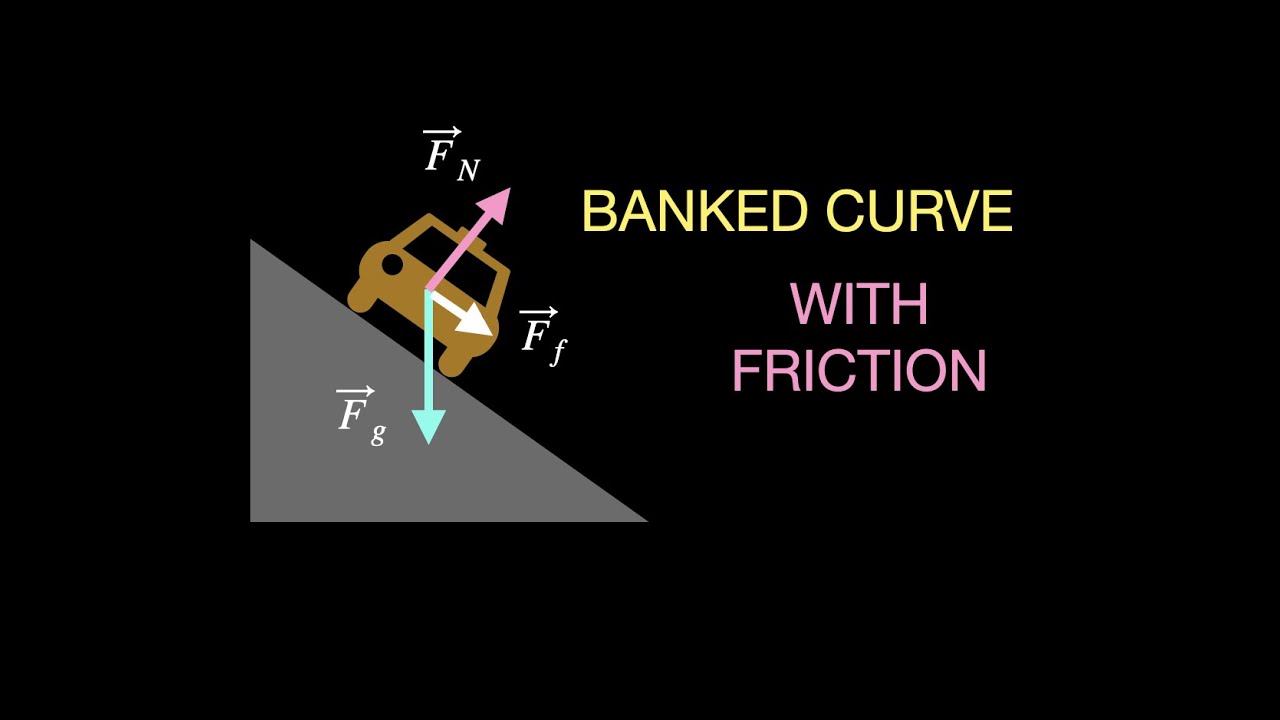
  • 📚 Free body diagrams are used to illustrate the forces at play on a banked curve versus a regular incline.
  • 🔄 The normal force on a banked curve is different from that on a regular incline, supporting more than just the weight of the object.
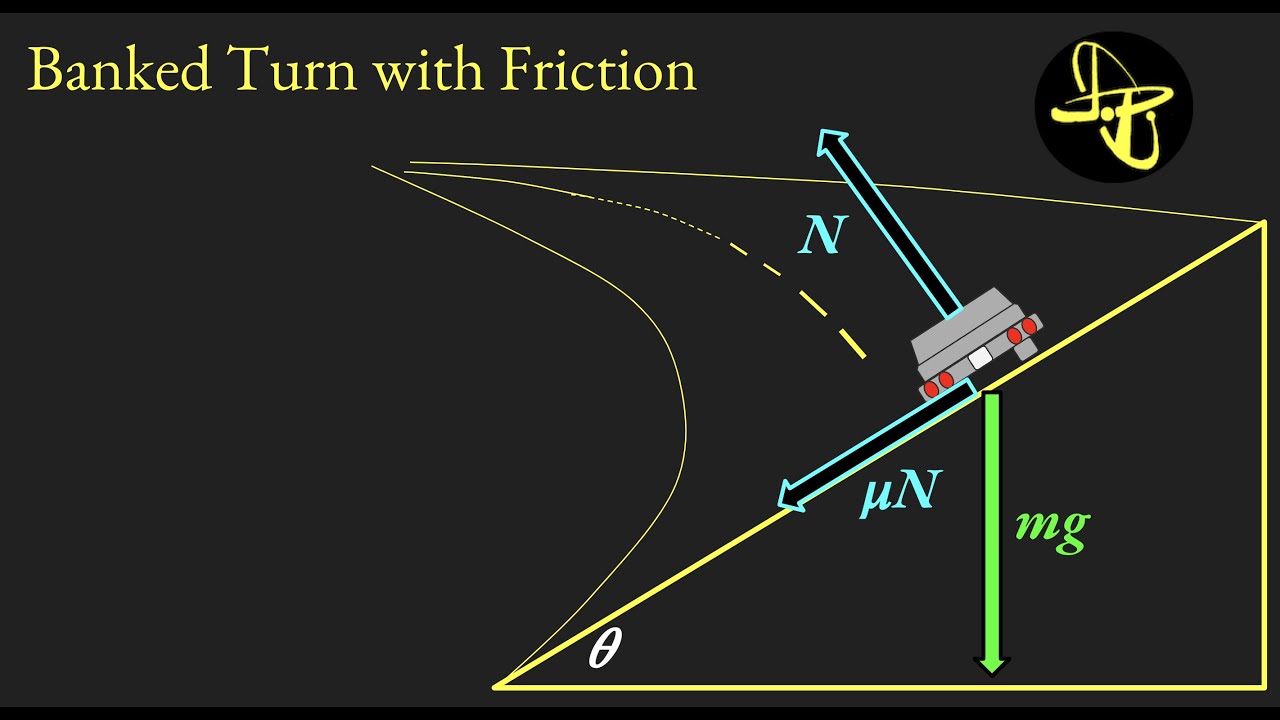
  • ⚖️ The normal force on a banked curve is calculated as mg/cosine(theta), where mg is the weight of the object and theta is the angle of the curve.
  • 🔄 The car's speed to maintain its position on the curve without sliding is found by setting the centripetal force equal to the component of the normal force.
  • 📉 The formula for the required speed is derived as v = √(rg * tan(theta)), where r is the radius, g is the acceleration due to gravity, and theta is the angle of the curve.
  • 🔢 Plugging in the values, the car should travel at 22.9 meters per second to maintain its position on the 15-degree banked curve without friction.
  • 🛣️ To increase the safe speed of the car on the curve, the angle of the bank must be increased, calculated using the arc tangent of (v^2/(rg)).
Q & A

  • What is the main focus of the video?

    -The main focus of the video is to explain the concept of banked curves and how to calculate the speed at which a car should travel on a frictionless banked curve to avoid sliding up or down.

  • What is the radius of the banked curve in the example given in the video?

    -The radius of the banked curve in the example is 200 meters.

  • What is the angle of the banked curve in the example?

    -The angle of the banked curve in the example is 15 degrees.

  • What is the difference between a regular incline and a banked curve?

    -A regular incline has a normal force perpendicular to the surface that supports only a portion of the weight due to gravity, while on a banked curve, the normal force supports the full weight of the object and provides the centripetal force necessary for circular motion.

  • Why is the normal force on a banked curve different from that on a regular incline?

    -The normal force on a banked curve is different because it has to support the full weight of the object and also provide the centripetal force needed for the circular motion, whereas on a regular incline, it only supports a portion of the weight.

  • What is the formula to calculate the speed at which a car should travel on a banked curve without sliding?

    -The formula to calculate the speed is v = √(rg * tan(theta)), where v is the speed, r is the radius of the curve, g is the acceleration due to gravity, and theta is the angle of the banked curve.

  • What is the calculated speed for the car to not slide up or down the banked curve in the example?

    -The calculated speed for the car to not slide up or down the banked curve in the example is 22.9 meters per second.

  • What is the relationship between the angle of the banked curve and the speed at which a car can safely travel?

    -The angle of the banked curve is directly related to the speed at which a car can safely travel. A larger angle allows for a higher speed without the car sliding up or down the curve.

  • How can the angle of the banked curve be adjusted to allow for a higher speed?

    -The angle of the banked curve can be increased to allow for a higher speed. The formula for calculating the required angle is theta = arctan(v^2 / (rg)), where v is the desired speed, r is the radius, and g is the acceleration due to gravity.

  • What angle should the road be banked at for a car to travel at a speed of 30 meters per second without sliding?

    -The road should be banked at an angle of approximately 24.62 degrees (or rounded to 24.7 degrees) for a car to travel at a speed of 30 meters per second without sliding.

Outlines
00:00
🚗 Understanding Banked Curves and Frictionless Motion

This paragraph introduces the concept of banked curves and their importance in physics, specifically when dealing with frictionless surfaces. It poses a problem where a car is traveling on a banked curve with a radius of 200 meters and an angle of 15 degrees. The challenge is to determine the speed at which the car should travel so that it neither slides up nor down the curve. The explanation involves distinguishing between regular inclined motion and banked curve motion, highlighting the difference in the way forces act on the car in both scenarios. The paragraph emphasizes the need to find a specific speed that allows the car to maintain its position on the curve without any frictional forces.

05:02
📚 The Physics of Normal Force on a Banked Curve

This section delves deeper into the physics behind banked curves, contrasting it with regular inclined surfaces. It explains how the normal force on a banked curve is not just supporting the weight of the object but also providing the necessary centripetal force for circular motion. The paragraph clarifies that the normal force on a banked curve is calculated as mg divided by cosine(theta), which is different from the regular incline where it's mg times cosine(theta). The significance of this difference is highlighted by comparing the normal force at a 45-degree angle in both scenarios. The paragraph also sets up the foundation for finding the critical speed at which the car will not slide on the banked curve.

10:05
🔍 Calculating the Critical Speed for a Banked Curve

Building upon the previous explanation, this paragraph focuses on calculating the exact speed at which a car can travel on a banked curve without sliding. It discusses the forces acting in the x-direction, particularly the x-component of the normal force, which is responsible for the centripetal acceleration. The paragraph uses the formula for centripetal acceleration (v^2/r = g * tan(theta)) to derive the speed required for the car to maintain its position on the curve. By substituting the given values for radius, gravitational acceleration, and the angle of the banked curve, the paragraph concludes with the calculation of the critical speed, which is found to be 22.9 meters per second.

15:05
🛣️ Determining the Optimal Banking Angle for a Given Speed

The final paragraph addresses the reverse problem: finding the banking angle required for a car to travel at a specific speed without sliding, in this case, 30 meters per second. It explains that increasing the banking angle allows for higher speeds on the curve. The paragraph guides through the mathematical process of finding the banking angle using the formula derived from the centripetal acceleration equation. By substituting the desired speed and the given radius into the formula, the paragraph calculates the new banking angle to be approximately 24.7 degrees, which would allow the car to safely travel at 30 meters per second without sliding up or down the banked curve.

Mindmap
Keywords
💡Banked Curves
Banked curves refer to roadways or race tracks designed with an incline on both sides to allow vehicles to negotiate turns without the need for friction to maintain their path. In the context of the video, banked curves are crucial for understanding how a car can travel on a curved path at a certain speed without sliding up or down the incline. The video script uses banked curves to illustrate the physical principles behind a vehicle's motion during a turn.
💡Frictionless
Frictionless is a term used to describe a surface or condition where there is no resistance to the motion of an object. In the video, the concept of a frictionless banked curve is essential as it simplifies the physics problem by eliminating the effects of friction, which allows the presenter to focus on the forces at play due to gravity and the banking of the curve.
💡Radius
The radius of a curve is the distance from the center of the circular path to any point on the path. In the video, the radius of 200 meters is a key parameter in calculating the speed at which a car should travel on a banked curve to maintain its position without sliding.
💡Incline
An incline is a sloping surface. The video script distinguishes between a regular incline, where an object would slide down due to gravity, and a banked curve, which is designed to counteract this sliding motion through its banking angle, allowing for stable travel at certain speeds.
💡Normal Force
Normal force is the force exerted by a surface that supports the weight of an object resting on it, acting perpendicular to the surface. In the context of the video, the normal force is critical on a banked curve as it not only supports the weight of the car but also provides the necessary centripetal force for circular motion, which is different from its role on a regular incline.
💡Centripetal Force
Centripetal force is the force that keeps an object moving in a circular path, directed towards the center of the circle. The video explains that on a banked curve, the normal force provides this centripetal force, which is essential for maintaining the car's position on the curve at the correct speed.
💡Tangential
Tangential relates to a direction that is tangent to a curve or circle, which in the context of the video, refers to the direction of the car's velocity as it travels along the banked curve. The script uses the tangent of the banking angle to calculate the required speed for stable travel.
💡Acceleration
Acceleration is the rate of change of velocity of an object. In the video, the term is used to describe the centripetal acceleration that a car experiences when traveling in a circular path on a banked curve, which is a key factor in determining the necessary speed to avoid sliding.
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. The video uses trigonometric principles, such as sine and cosine, to relate the forces acting on the car to its speed and the banking angle of the curve.
💡Arc Tangent
Arc tangent, also known as inverse tangent, is a trigonometric function that returns the angle whose tangent is a given number. In the video, arc tangent is used to solve for the banking angle required for a car to travel at a specific speed without sliding, demonstrating the application of trigonometry in physics problems.
Highlights

The video focuses on banked curves and the physics behind them.

A car travels on a frictionless banked curve of radius 200 meters, banked at an angle of 15 degrees.

The goal is to find the speed at which the car will not slide up or down the curve.

Banked curves differ from regular inclines in the motion and forces involved.

A free body diagram is used to analyze forces on a banked curve.

On a banked curve, the normal force supports more than the weight of the object.

The normal force on a banked curve is mg divided by cosine theta.

The normal force on a banked curve is larger due to supporting the full weight and providing centripetal force.

The car's speed must be precise to maintain its position on the curve without friction.

The net force in the y-direction is zero for the car to maintain its position.

The net force in the x-direction is the centripetal force causing circular motion.

The speed formula v = sqrt(rg * tan(theta)) is derived to calculate the car's speed on the curve.

The calculated speed for the car to not slide is 22.9 meters per second.

The video explains how increasing the banking angle allows for higher speeds without sliding.

An equation is provided to calculate the required banking angle for a given speed.

The calculated angle for a car to travel at 30 meters per second without sliding is 24.62 degrees.

Transcripts

Browse More Related Video

Banked Turn with Friction - Physics of Speed Limits on Banked Curves

Car on a banked curve

Banked Curve Physics - Uniform Circular Motion

banked curves and circular motion explained

Banked Curve with Friction: Finding Maximum and Minimum Speed

Maximum Speed Around a Banked Curve WITH Friction

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Banked CurvesPhysicsFrictionlessVehicle DynamicsOptimal SpeedCircular MotionTrigonometryCentripetal ForceTrigonometric RatiosVehicle Stability