Banked Turn with Friction - Physics of Speed Limits on Banked Curves
TLDRThis educational script explores the physics behind calculating the maximum speed a car can safely navigate a banked turn without skidding. It breaks down the forces at play, including gravity, normal force, and friction, and how they relate to the angle of the incline. The script uses trigonometric functions to derive equations for the vertical and horizontal forces acting on the car, leading to an expression for the maximum speed in terms of the radius of the curve, the angle of the bank, and the coefficient of friction. It also discusses the implications of banking a curve correctly versus incorrectly, and how it affects the car's stability and speed.
Takeaways
- 🚗 The maximum speed a car can take around a banked turn is determined by analyzing the forces acting on the car.
- 🧭 The forces considered are gravity, normal force, and friction, with the normal force and friction having both horizontal and vertical components.
- ⚖️ The vertical components of the normal force and friction must balance out with gravity to prevent vertical acceleration.
- 🔄 The horizontal components of the normal force and friction combine to provide the centripetal force necessary for circular motion.
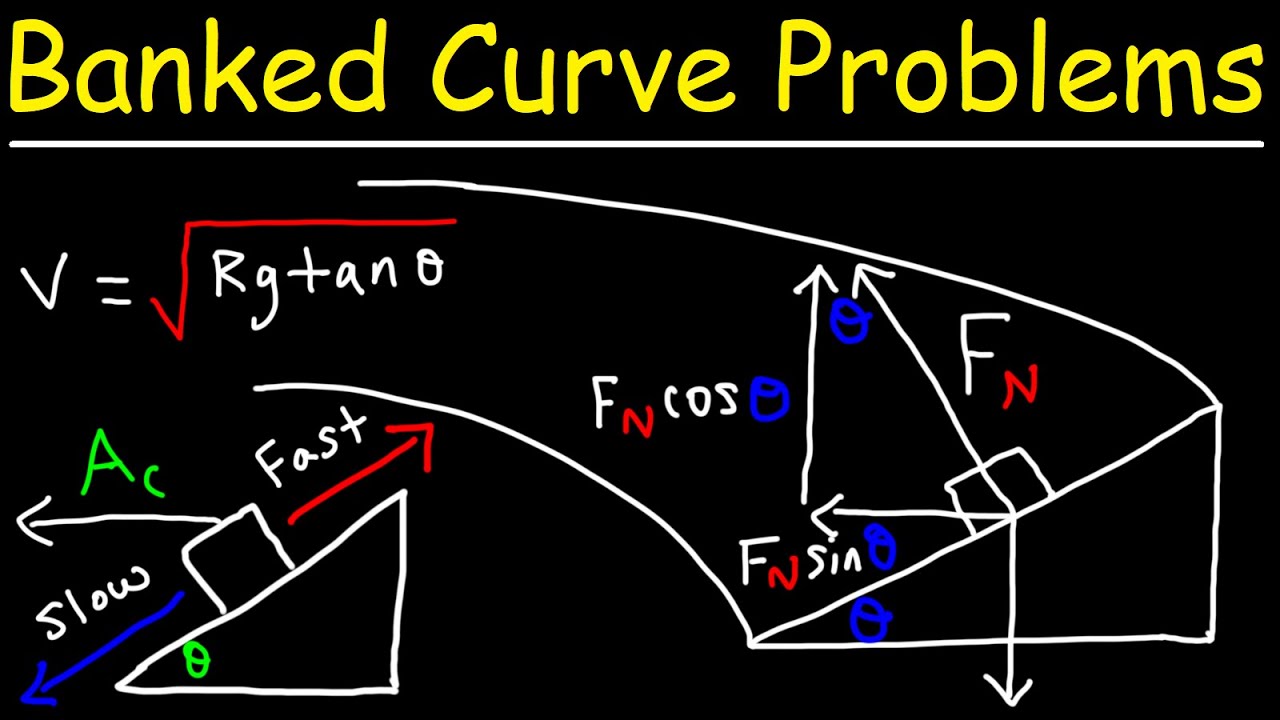
- 📐 The angle theta is crucial as it represents both the angle of the banked turn and the angle by which the normal force is inclined from the vertical.
- 🔄 By balancing the vertical forces, an equation for the normal force (N) can be derived in terms of mass (m), gravity (g), and the angle theta.
- 🔄 The horizontal forces are combined to equate to the centripetal acceleration, which is expressed as v^2 / r, where v is the speed and r is the radius of the curve.
- 🔢 By substituting the expression for N into the horizontal force equation, an equation for v^2 (the square of the speed) can be found in terms of the radius, angle, and coefficient of friction.
- 📈 The derived relationship allows for the calculation of the maximum speed for a given bank angle, radius of curvature, and coefficient of friction.
- 📊 A graph can be plotted to visualize how the maximum speed varies with the angle of the banked turn, demonstrating the effect of banking on speed.
Q & A
What is the main topic of the script?
-The script discusses how to calculate the maximum speed a car can take around a banked turn on a road.
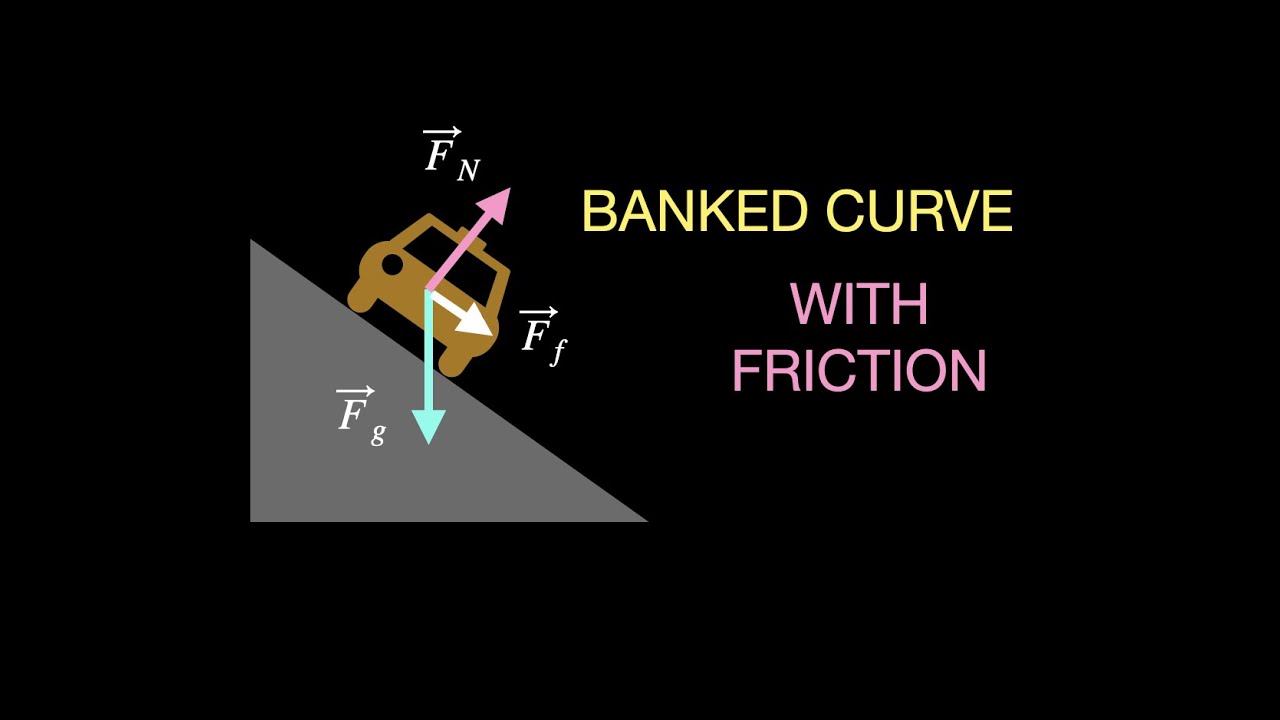
What are the three forces acting on the car during the process of taking a banked turn?
-The three forces acting on the car are gravity, the normal force from the road, and friction.
How does the normal force relate to the angle of the incline?
-The normal force makes an angle theta with the vertical, which is the same angle that the incline makes from the horizontal.
What is the direction of friction when the car is moving at maximum speed around the banked turn?
-Friction acts down the incline towards the bottom when the car is moving at maximum speed.
What is the relationship between the vertical component of the normal force and the angle of the incline?
-The vertical component of the normal force is given by n cosine theta, where n is the normal force and theta is the angle of the incline.
How is the vertical component of the friction force related to the angle of the incline?
-The vertical component of the friction force is given by mu n sine theta, where mu is the coefficient of friction, n is the normal force, and theta is the angle of the incline.
Why do the vertical forces on the car add up to zero?
-The vertical forces add up to zero because the car does not accelerate up or down, maintaining a constant vertical velocity.
What are the two unbalanced forces acting in the horizontal direction?
-The two unbalanced forces in the horizontal direction are the horizontal component of the normal force (n sine theta) and the horizontal part of the friction force (mu n cosine theta).
What is the formula for centripetal acceleration in the context of the car taking a banked turn?
-The formula for centripetal acceleration is v squared over r, where v is the speed of the car and r is the radius of the curve.
How can you determine the maximum speed a car can take around a banked turn?
-You can determine the maximum speed by using the derived equations that relate the normal force, friction, and the car's mass to the speed, and then solving for v (velocity).
What happens to the maximum speed as the angle of the bank increases?
-As the angle of the bank increases, the maximum speed at which the car can take the curve also increases, up to a certain point.
What is the effect of banking the turn the wrong way on the maximum speed?
-Banking the turn the wrong way decreases the maximum speed at which the car can safely take the curve, making it easier for the car to skid out.
What is the significance of the mass of the car in the context of skidding out of a turn?
-The mass of the car is not relevant to whether the car would skid out of the turn, as it cancels out in the equations used to determine the maximum speed for a given turn.
Can you provide an example of how the maximum speed varies with the angle of the bank?
-An example given in the script is an exit ramp with a 100-meter radius, where at a bank angle of 0 degrees, the car could go 30 m/s, and at about 45 degrees, the maximum speed increases to around 150 m/s.
Outlines
🚗 Calculating Maximum Speed for a Banked Turn
This paragraph delves into the physics of determining the maximum speed a car can safely take around a banked turn. It begins by identifying the forces acting on the car: gravity, the normal force from the road, and friction. The normal force is shown to be at an angle theta with the vertical, which is the same as the incline's angle from the horizontal. The vertical components of the normal force and friction are calculated using trigonometric functions, and it's established that these forces must sum to zero to prevent vertical acceleration. The horizontal forces are also considered, leading to an equation involving centripetal acceleration. The goal is to solve for the maximum speed, which is approached by combining the equations for the forces and acceleration. The paragraph concludes with setting up the equations to solve for speed, emphasizing the importance of the bank angle, friction coefficient, and road radius in determining the maximum safe speed.
📈 Analyzing the Relationship Between Bank Angle and Speed
The second paragraph continues the discussion on the physics of a car taking a banked turn, focusing on how to calculate the normal force and subsequently the maximum speed. It explains the process of factoring out the normal force from the equations and substituting it back to eliminate it as an unknown variable. The mass of the car is shown to cancel out when considering the risk of skidding, leading to a formula for speed squared in terms of the radius of the curve, the angle of the bank, and the coefficient of friction. The paragraph then extends the analysis by graphing the relationship between the maximum speed and the bank angle for a given radius of curvature and friction coefficient. It illustrates that as the bank angle increases, the maximum safe speed also increases, up to a certain point where further banking would cause the car to skid out. Interestingly, the graph also shows that banking the curve in the wrong direction decreases the maximum safe speed and could potentially cause the car to slide down the incline if banked too much in the incorrect direction.
📊 Visualizing the Impact of Incorrect Banking on Speed
The final paragraph provides a visual representation of how incorrect banking affects the maximum speed a car can take around a curve. It describes a scenario where the radius of curvature is fixed, and the effects of varying the bank angle on speed are graphed. The graph shows that if the curve is not banked at all, the car can travel at a certain speed without skidding. As the curve is banked correctly, the maximum speed increases, reaching a peak at around 45 degrees of bank angle. However, if the curve is banked in the wrong direction, the graph indicates a decrease in the maximum speed, and beyond a certain angle, the car would not be able to maintain traction and would start to slide down the incline, even when stationary. This paragraph emphasizes the importance of proper banking in maintaining vehicle stability and speed around turns.
Mindmap
Keywords
💡Banked Turn
💡Gravity
💡Normal Force
💡Friction
💡Vertical and Horizontal Forces
💡Centripetal Acceleration
💡Coefficient of Friction
💡Mass
💡Radius of Curvature
💡Angle of Incline
Highlights
The process of finding the maximum speed a car can take around a banked turn involves analyzing the forces acting on the car.
Gravity, normal force, and friction are the primary forces considered in this analysis.
The normal force makes an angle theta with the vertical, which is the same as the angle of the incline from the horizontal.
Vertical forces acting on the car are resolved into components to understand their balance.
Friction acts down the incline towards the bottom, aiding in maintaining the car's speed around the turn.
The vertical component of the normal force is given by n cosine theta.
The vertical component of friction force is calculated using y sine theta.
Vertical forces must sum to zero as the car does not accelerate up or down.
Horizontal forces include the normal force's horizontal component and the horizontal part of friction.
The sum of horizontal forces contributes to the centripetal acceleration required for circular motion.
Centripetal acceleration is expressed as v squared over r, directed towards the center of the circle.
The goal is to solve for the maximum speed the car can take around the curve using the derived equations.
By solving the equations, one can find expressions for the normal force and subsequently the speed.
The mass of the vehicle cancels out in the equation for skidding out of the turn.
An expression for v squared is derived, which can be used to find the speed without taking the square root.
The derived relationship allows determining the speed based on the angle of the ramp, coefficient of friction, and radius of curvature.
A graph can be plotted to show the maximum speed versus the angle of the banked turn for a given radius.
Banking the turn properly increases the maximum speed a car can take around the curve.
If the turn is banked the wrong way, the car's maximum speed decreases, and it's more likely to skid out.
The car would start to slide down the incline if banked more than approximately 42 degrees in the wrong direction.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: