AP Physics Workbook 3.E Maximum speed over the top
TLDRThe video script discusses a physics problem involving a car passing over a bump and following a circular arc. It explains the forces acting on the car at the top of the hill, focusing on the balance between gravitational force and the normal force. The key concept is that at the top, the normal force can be considered zero for a car moving at the maximum speed, and the speed is determined by the gravitational force and the radius of the circular path. The problem is solved using Newton's second law and centripetal acceleration, highlighting that the maximum speed depends on the radius and gravitational force, not the mass of the object.
Takeaways
- 📚 The script covers solutions for AP Physics, focusing on unit three which deals with circular motions and gravitation.
- 📈 It discusses a scenario involving a car of mass M going over a bump that forms an arc of a circle with radius R.
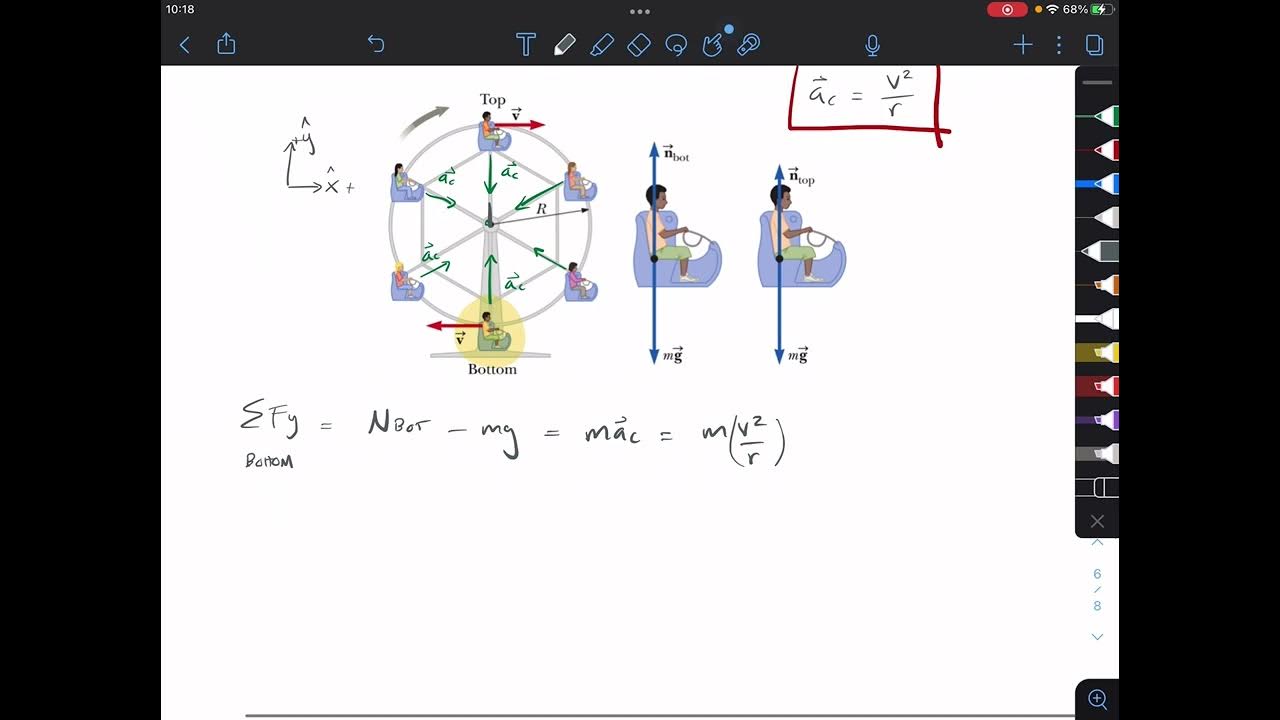
- 📖 A key part of the analysis involves drawing a Freebody Diagram to show and label the forces acting on the car without their components, emphasizing the importance of representing the relative magnitude of these forces accurately.
- 🖥 At the top of the hill, the forces acting on the car are broken down into the force of gravity and the normal force, with an important distinction made between their magnitudes to reflect the car's motion.
- 🚗 The solution process begins with applying Newton's second law, leading to an expression for the magnitude of the car's speed at the top of the hill, using the relationship between acceleration, force, and mass.
- 📉 The derivation simplifies to show that the car's speed depends only on the radius of the circle (R) and the gravitational constant (g), highlighting that mass is irrelevant for this calculation.
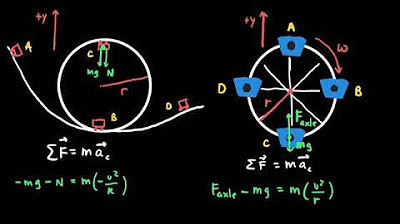
- ✅ An important assumption made in the calculation is setting the normal force to zero at the top of the hill, justified by the fact that gravity is the only force providing centripetal acceleration at that point.
- 🛥 For a truck of mass 2M going over the same bump, it's demonstrated that the magnitude of speed required to not lose contact with the road does not depend on the mass but only on the radius of the arc, confirming the same speed requirement as for the car.
- 📏 The script emphasizes that the derived formula for velocity (🛥 V = √(Rg)) is universal for any object undergoing circular motion under similar conditions, underscoring the principle that only the radius of the motion's path matters, not the mass of the moving object.
- 📢 Concludes with the generalization that the key to solving circular motion and gravitation problems in physics often involves understanding and applying the fundamental principles of forces and motion, rather than memorizing specific formulas.
Q & A
What scenario is being discussed in the transcript?
-The transcript discusses a scenario where a car of mass M passes through a bump in a roadway and follows the arc of a circle with radius R.
What is the significance of the Freebody diagram in this context?
-The Freebody diagram is significant as it represents the car at the top of the hill and shows the forces exerted on the car, helping to visualize and calculate the physical interactions.
What are the forces acting on the car at the top of the hill?
-At the top of the hill, the forces acting on the car are gravity (mg) and the normal force (FN).
How is the magnitude of the car's speed at the top of the hill determined?
-The magnitude of the car's speed at the top of the hill is determined using Newton's second law and the concept of centripetal acceleration, which is given by the formula V = sqrt(G * R), where G is the acceleration due to gravity and R is the radius of the circle.
Why is the normal force (FN) considered to be zero at the top of the hill?
-The normal force (FN) is considered to be zero at the top of the hill because, for the car to just make it over the top without any assistance from the track, the only force acting downwards would be the force of gravity.
What happens to the car's speed if the mass is doubled?
-The car's speed does not depend on its mass. Therefore, if the mass is doubled, the speed required to make it to the top of the hill remains the same, as it only depends on the radius and the acceleration due to gravity.
How does the concept of centripetal acceleration apply to this scenario?
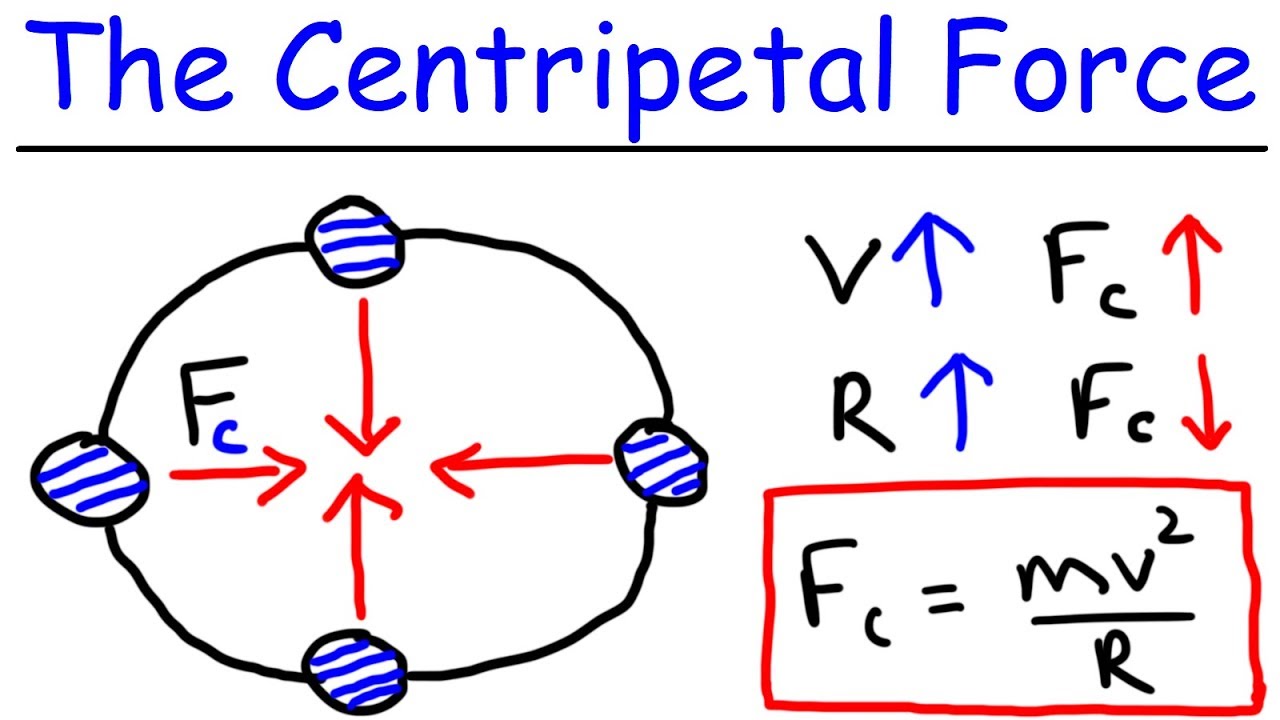
-Centripetal acceleration is the acceleration that keeps an object moving in a circular path. In this scenario, it is provided by the net force acting towards the center of the circle, which is the difference between the gravitational force and the normal force.
What is the role of Newton's second law in solving this problem?
-Newton's second law, which states that the net force on an object is equal to the mass of the object multiplied by its acceleration (F = ma), is used to derive the expression for the car's speed at the top of the hill and to set up the equation for the forces acting on the car.
Why are the relative lengths of the vectors in the Freebody diagram important?
-The relative lengths of the vectors in the Freebody diagram are important because they reflect the relative magnitudes of the forces. This helps in visualizing the net force acting on the car and in performing the calculations accurately.
How does the force of gravity act at the top of the loop?
-At the top of the loop, the force of gravity acts downwards and towards the center of the circle. This force is responsible for providing the necessary centripetal acceleration for the car to continue moving in a circular path.
What is the significance of setting FN equal to zero in the calculations?
-Setting FN equal to zero in the calculations signifies the condition where the car is just able to make it over the top of the hill without losing contact with the road. This is a critical condition for determining the minimum speed required for the car to pass over the bump.
Outlines
🚗 Analyzing Circular Motion and Gravitation
This paragraph discusses the analysis of a car performing circular motion over a bump in the road. The focus is on the forces acting on the car at the top of the hill, specifically when the car is at the apex of its circular path. The scenario involves a car of mass M following the arc of a circle with radius R. The task is to draw a Freebody diagram, illustrating and labeling the forces exerted on the car, such as gravity and the normal force. It emphasizes the importance of vector representation and the relative magnitude of forces. The paragraph also introduces the concept of centripetal acceleration and how it can be derived from Newton's second law of motion, setting up the foundation for solving the problem.
📚 Applying Newton's Second Law to Circular Motion
This paragraph delves into the application of Newton's second law to the circular motion problem introduced earlier. It explains how to derive an expression for the car's speed at the top of the hill by setting up the equation with the given forces. The paragraph clarifies the relationship between the normal force and the force of gravity, highlighting that they are not equal at the top of the hill. It provides a step-by-step explanation of the calculations, starting with the substitution of centripetal acceleration (V^2/R) and leading to the final expression for the speed of the car (V = √(GR)). The explanation also touches on why the normal force can be considered zero at the top of the hill, as it is the only point where gravity is the sole force acting on the car.
🔄 Understanding the Role of Mass and Radius in Circular Motion
This paragraph examines the role of mass and radius in determining the speed of an object in circular motion. It reiterates that at the top of a circular path, the speed of the car depends solely on the radius of the circle and the force of gravity, with mass having no influence. The explanation extends to different scenarios, such as a truck with mass 2m, and emphasizes that the maximum speed required to navigate the hill without losing contact with the road remains the same, as it is determined by the radius and gravitational constant. The paragraph concludes by generalizing the concept to other circular motion scenarios, such as rollercoasters and airplanes, reinforcing that the speed depends only on the radius, not the mass.
📈 Deriving Speed Equation for Circular Motion
The final paragraph synthesizes the information from the previous discussions and presents a general equation for the speed of an object in circular motion. It introduces the concept of function notation to express the relationship between velocity (V) and the radius (R) of the circular path. The equation V = √(GR) is derived, where G is the gravitational constant. This equation illustrates that the speed of an object in circular motion is independent of its mass and solely reliant on the radius of the circle and the gravitational force. The paragraph reinforces the understanding that the mass of the object does not affect the required speed to maintain circular motion, as long as the radius and gravitational constant remain constant.
Mindmap
Keywords
💡Circular Motion
💡Centripetal Acceleration
💡Freebody Diagram
💡Newton's Second Law
💡Force of Gravity
💡Normal Force
💡Maximum Speed
💡Radius
💡Vector
💡Truck Scenario
Highlights
The scenario involves a car of mass M passing through a bump and following a circular arc of radius R.
At the top of the hill, the car experiences maximum speed and specific forces acting on it.
A Freebody diagram is used to visualize and label the forces exerted on the car, with the relative lengths of vectors representing the relative magnitudes of the forces.
Newton's second law is applied to analyze the forces acting on the car at the top of the hill.
Centripetal acceleration is defined as the magnitude of acceleration and is used in the calculations.
The force of gravity (mg) and the normal force (FN) are the two forces considered in the scenario.
At the top of the hill, the normal force (FN) is equal to zero, and the car's weight (mg) provides the necessary centripetal force.
The equation G = V^2/R is derived to find the speed of the car at the top of the hill.
The mass of the car cancels out in the equation, indicating that the maximum speed depends only on the radius and gravitational acceleration.
The speed required for the car to make it over the top without losing contact with the road is determined by the radius and gravity, not the mass.
A truck with mass 2m would have the same maximum speed as the car when passing over the same bump due to the same radius.
The problem-solving approach can be generalized to other scenarios such as rollercoasters or airplanes.
The speed around a circular path depends solely on the radius and gravitational acceleration, not on the mass of the object.
The use of a Freebody diagram and Newton's second law allows for a detailed analysis of circular motion.
The concept of centripetal acceleration is crucial for understanding the forces involved in circular motion.
The mathematical relationship between speed, radius, and gravitational acceleration is explored through the derived equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: