AT&T Archives: Matter Waves, Holden and Germer on Wave Nature and the Davisson-Germer Experiment
TLDRThis script explores the wave-particle duality of matter and light, challenging the viewer to accept that particles, like electrons, exhibit wave-like behavior. It recounts de Broglie's hypothesis from 1923, supported by Einstein, which was later confirmed by diffraction experiments. The script delves into electron microscopy, diffraction phenomena, and the use of gratings to demonstrate wave properties. It highlights the significance of de Broglie's relation, \( \lambda = \frac{h}{p} \), in predicting electron wavelengths and the practical applications of this knowledge in understanding atomic structures and the arrangement of atoms on crystal surfaces.
Takeaways
- 🌟 Light, an electromagnetic wave, can behave like a stream of particles known as photons.
- 🌌 Particles of ordinary matter, such as electrons, can exhibit wave-like behavior, a concept that was initially shocking and counterintuitive.
- 🎓 Louis de Broglie proposed in 1923 that particles might have wave-like properties, an idea that was initially met with skepticism but later supported by Albert Einstein.
- 🔬 Experiments by Davisson and Germer in New York City and G.P. Thomson in Cambridge, England, demonstrated electron diffraction, supporting de Broglie's hypothesis.
- 💡 Waves can be diffracted, bending around obstacles and not casting sharp shadows, unlike particles which would create distinct shadows.
- 📸 The electron microscope uses the wave-like properties of electrons to create images, showing diffraction patterns rather than sharp-edged shadows.
- 🛠 The diffraction of light by a ruled grating can be used to understand the wave-like properties of matter, as the grating scatters light waves in specific directions based on wavelength.
- 📏 De Broglie's relation, λ = h/p, predicts the wavelength of matter waves based on their momentum, with h being Planck's constant and p the momentum.
- 🔭 To observe electron diffraction, a grating with spacing comparable to the electron wavelength is needed, which can be achieved using the regular arrangement of atoms on a crystal surface.
- 🧬 The wave-like behavior of material particles is fundamental to understanding atomic and molecular structures and is a cornerstone of modern physics.
- 🔬 Dr. Lester Germer's experiments at Bell Telephone Laboratories further confirmed the wave nature of electrons and their use in studying atomic arrangements.
Q & A
What was the initial shock that the speaker mentioned at the beginning of the script?
-The initial shock referred to the concept that light, an electromagnetic wave, behaves in some ways like a stream of particles known as photons.
What fundamental idea did the speaker propose regarding particles of ordinary matter?
-The speaker proposed that particles of ordinary matter behave in some ways like waves, not in the sense of physical movement up and down, but in a more fundamental way.
Who suggested the wave nature of particles in 1923 and what was his motivation?
-Louis de Broglie suggested the wave nature of particles in 1923. His idea grew out of comparing the behavior of matter with the behavior of light.
Why was there initial resistance to Louis de Broglie's idea at the University of Paris?
-Louis de Broglie's examiners at the University of Paris were reluctant to accept his idea because they considered it a foolish idea. He only received his degree due to Albert Einstein's support.
What experiments provided evidence supporting the wave nature of particles?
-Diffraction experiments conducted independently by Davison and Germer in New York City and G.P. Thomson in Cambridge, England, provided evidence supporting the wave nature of particles.
How do waves typically interact with barriers and what is the expected outcome?
-Waves typically bend around barriers, causing diffraction and preventing the formation of sharp shadows. If an object is smaller than the wavelength of the waves, it can cast no shadow at all.
How does the behavior of particles differ from waves when interacting with an obstacle?
-When particles such as droplets of paint from a spray gun are shot at an object, they either hit the object or miss it, resulting in a sharp shadow. This is in contrast to waves, which bend around obstacles.
What is the significance of diffraction patterns in understanding the wave-like behavior of particles?
-Diffraction patterns are evidence of wave-like behavior. When particles such as electrons create diffraction patterns, it suggests that they are behaving like waves, bending around obstacles and interfering with each other.
What is the de Broglie relation and how does it relate to the wavelength of particles?
-The de Broglie relation states that the wavelength (λ) of a particle is given by Planck's constant (h) divided by the particle's momentum (p), expressed as λ = h/p. This relation suggests that particles can exhibit wave-like properties with wavelengths inversely proportional to their momentum.
How can the wave-like behavior of particles be experimentally observed using crystals?
-The wave-like behavior of particles can be observed by directing a beam of particles, such as electrons, at a crystal. The regular arrangement of atoms on the crystal surface acts as a grating, causing the particles to diffract and form a pattern of spots on a screen, indicative of wave behavior.
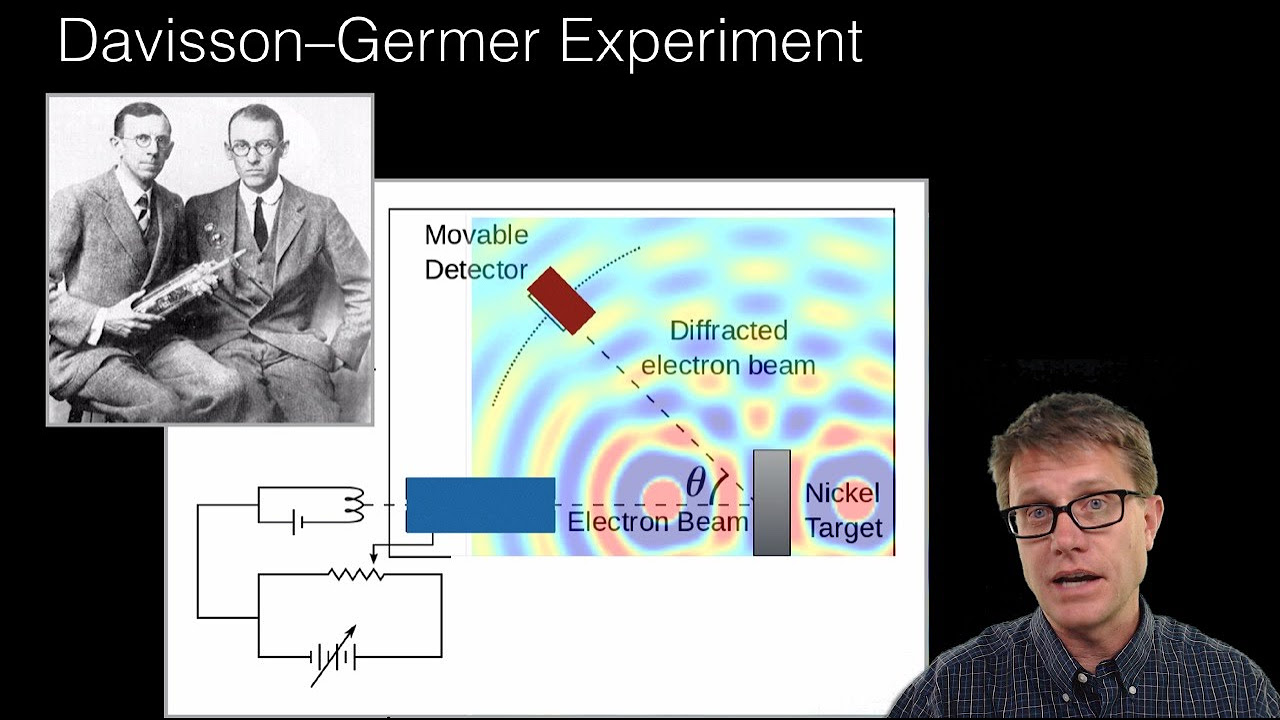
What is the significance of the Davisson-Germer experiment and its contribution to the understanding of wave-particle duality?
-The Davisson-Germer experiment was significant because it provided direct evidence for the wave nature of electrons. By observing electron diffraction patterns on a crystal surface, they confirmed de Broglie's hypothesis and contributed to the foundation of quantum mechanics.
How did G.P. Thomson's experiment differ from the Davisson-Germer experiment and what did it demonstrate?
-G.P. Thomson's experiment involved shooting a beam of electrons through a thin gold foil rather than reflecting them off a crystal surface. This experiment demonstrated that electrons passing through the foil were diffracted, further confirming their wave-like nature.
What role do x-rays play in demonstrating the wave-like properties of matter?
-X-rays, which have wavelengths comparable to the spacing between atoms in a crystal, can be diffracted when they pass through a crystal or a foil. The diffraction patterns produced by x-rays are similar to those produced by electrons, providing further evidence for the wave-like properties of matter.
How have the wave-like properties of particles contributed to our understanding of atoms and molecules?
-The wave-like properties of particles, particularly electrons and neutrons, have been fundamental in developing our understanding of the behavior of individual atoms and how they form molecules. This understanding is crucial for the study of chemistry and material science.
Outlines
📚 Introduction to Wave-Particle Duality
The paragraph introduces the concept of wave-particle duality, explaining that light behaves like both a wave and a stream of particles called photons. It then challenges the viewer to accept that particles of matter can also exhibit wave-like properties. The script references Louis de Broglie's 1923 thesis suggesting matter waves and the diffraction experiments by Davisson and Germer, and G. P. Thomson that confirmed this theory. The explanation includes the behavior of waves, such as diffraction, and contrasts it with the behavior of particles, as observed in electron microscopes.
🌟 Light and Electron Diffraction
This paragraph explores the diffraction of light and electrons, showing that both can create patterns similar to one another, suggesting a wave-like behavior. It discusses the interference of light waves and how this can be used to confirm the presence of waves. It also touches on the diffraction grating and how it scatters light to create a spectrum, depending on the wavelength. The paragraph concludes by proposing that matter, if it behaves like waves, should also show a similar diffraction pattern when passed through a grating with the appropriate spacing.
🧬 De Broglie's Equation and Electron Diffraction
The paragraph delves into De Broglie's hypothesis that matter waves could be described by a wavelength given by h/p, where h is Planck's constant and p is the momentum of the particle. It provides calculations for the wavelength of an electron based on its mass and velocity, suggesting that the wavelength is comparable to the size of an atom. It then discusses the practicality of creating a grating with atomic-scale spacing and how the regular arrangement of atoms on a crystal surface can act as such a grating for electron diffraction experiments.
💡 Observing Electron Diffraction Patterns
This section describes an experiment where electrons are accelerated and directed at a crystal surface, resulting in a diffraction pattern on a fluorescent screen. The pattern's size changes with the voltage applied to the electron gun, which affects the electron's energy, momentum, and wavelength. The experiment is used to study the arrangement of atoms on the crystal surface and to confirm the wave-like nature of electrons, as first demonstrated by Davisson and Germer.
🔬 Early Electron Diffraction Experiments
The paragraph recounts the earlier, more laborious methods of observing electron diffraction, where the positions and voltages of diffraction beams were manually measured. It contrasts these methods with the more convenient use of a fluorescent screen for observing intensity maxima. The paragraph also discusses how the initial experiments were conducted without prior knowledge of De Broglie's theory but were later found to be in agreement with it.
🌐 Wave-Like Behavior of Matter
The final paragraph broadens the discussion to include not just electrons, but other particles such as helium atoms and neutrons, which also exhibit wave-like properties when diffracted from crystals. It highlights that this wave-like behavior is foundational to our understanding of matter, atoms, and molecules. The paragraph concludes with a mention of how the wave-like nature of particles is used in various research fields and how it has been experimentally verified for different types of particles.
Mindmap
Keywords
💡Electromagnetic Wave
💡Photons
💡Wave-Particle Duality
💡Diffraction
💡Electron Microscope
💡De Broglie Wavelength
💡Crystal Lattice
💡Davisson-Germer Experiment
💡Grating
💡X-rays
💡Neutron Diffraction
Highlights
Light behaves both as an electromagnetic wave and a stream of particles, known as photons.
Ordinary matter particles exhibit wave-like behavior, a concept introduced by Louis de Broglie in 1923.
Albert Einstein supported de Broglie's wave-particle duality theory, which was initially met with skepticism.
Davisson and Germer, and G. P. Thomson conducted diffraction experiments confirming the wave nature of particles.
Waves can be diffracted, unlike particles, which either hit an object or do not, creating a shadow.
Electron microscopes use the wave-like properties of electrons to create enlarged shadows of tiny objects.
Electrons exhibit diffraction patterns, behaving like waves when creating images in electron microscopes.
De Broglie's relation (λ = h/mv) predicts the wavelength of matter particles based on their momentum.
To observe wave-like properties of matter, a grating with lines spaced similarly to the wavelength of the particles is required.
Crystals have a natural grating formed by the regular arrangement of atoms on their surface, suitable for electron diffraction experiments.
Dr. Lester Germer's experiment with electrons bouncing off a crystal surface demonstrated the wave nature of electrons.
By adjusting the voltage, the size of the electron diffraction pattern can be controlled, reflecting changes in electron wavelength.
The Davisson-Germer experiment was the first to observe electron diffraction, confirming de Broglie's theory.
G. P. Thomson's experiment with electrons passing through gold foil showed a diffraction pattern similar to that of X-rays.
X-rays and electrons both exhibit wave-like properties when scattered by atoms in a foil, indicating a commonality in their behavior.
The wave-like behavior of material particles is foundational to understanding atomic and molecular structures.
De Broglie's theory has been extended to show wave-like properties for other particles, such as helium atoms and neutrons.
The wave-particle duality is now a cornerstone of modern physics and is utilized in various research fields.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: