4. Wave-Particle Duality of Matter; Schrödinger Equation

The script begins with an introduction to MIT OpenCourseWare, a free educational resource supported by donations, and then transitions into a classroom setting where Professor Catherine Drennan is discussing the photoelectric effect. The photoelectric effect is a phenomenon where light ejects electrons from a material, and it is explained through the concept of photons having energy. The class explores the conditions under which electrons are ejected, such as the energy of incoming photons needing to be equal to or greater than the work function of the material. The discussion includes a practical example of adding photons with insufficient energy and emphasizes that this does not result in electron ejection, akin to individual knowledge required to pass an exam.

This paragraph delves deeper into the photoelectric effect, discussing the relationship between photons, their energy, and the ejection of electrons from a metal surface. It introduces the concept that each photon must have enough energy to meet the threshold required to eject an electron. The script mentions an in-class demonstration using a zinc surface and different light sources with varying wavelengths to predict and observe electron ejection. The paragraph also covers the terminology and concepts relevant to solving problems related to the photoelectric effect, such as the energy of photons, the kinetic energy of electrons, and the importance of understanding units like eV and joules.

The script describes an in-class experiment aimed at demonstrating the photoelectric effect. The experiment involves shining different light sources with varying wavelengths onto a zinc surface to see if they can eject electrons. The calculations for the energy of photons emitted by a UV lamp and a red laser pointer are detailed, with the UV light found to have sufficient energy to eject electrons while the red light does not. The experiment also includes a calculation of the number of photons emitted by a laser in 60 seconds, given an intensity of one milliwatt, resulting in a large number of photons.

This section of the script discusses the dual nature of light, which exhibits properties of both a wave and a particle. It explains how the photoelectric effect provided evidence for light's particle-like properties, with quantized energy in the form of photons. The script also touches on the concept of photons having momentum, as proposed by Einstein, and the related experiments by Arthur Compton. The discussion then shifts to the wave-like properties of matter, introduced by de Broglie, who suggested that particles like electrons could also exhibit wave-like behavior, with wavelengths calculated based on their momentum.

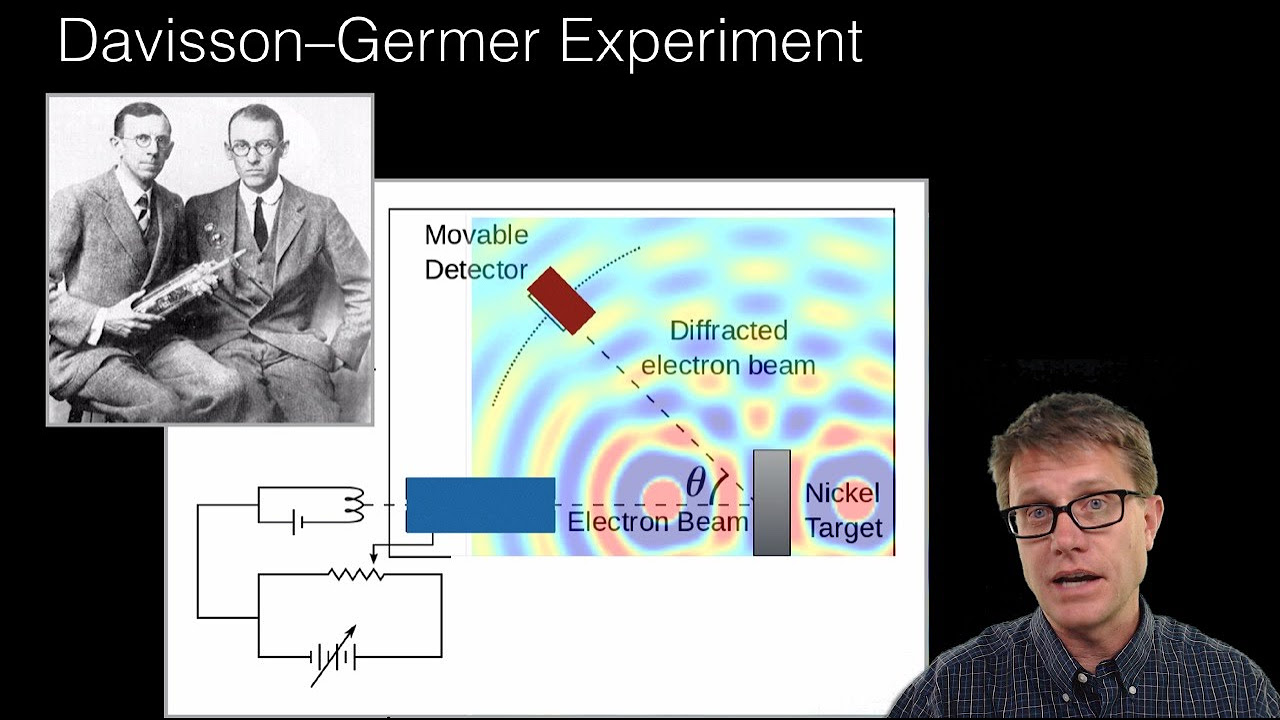
The script explores the wave-like properties of matter further by comparing the calculated wavelengths of everyday objects, such as a baseball, with that of an electron. It explains that while the wavelength of a baseball is too small to detect, the wavelength of an electron is significant when compared to the size of atoms. This makes the wave-like properties of electrons observable and important in the context of atomic and subatomic structures. The paragraph also discusses the observation of diffraction patterns produced by electrons, which is a wave-like property, and the historical significance of this discovery by scientists like JP Thomson.

This part of the script discusses the importance of quantum mechanics in modern research and applications. It highlights the unique properties of small particles, such as quantum dots, which have discrete energy levels and emit light of specific energies when electrons transition between these levels. The script mentions ongoing research in the Bawendi Lab at MIT, where quantum dots are being developed for medical applications, such as tumor identification during surgery. The potential of quantum mechanics in developing new materials, batteries, and electrodes for solving energy problems is also emphasized.

The script introduces the Schrodinger equation, a fundamental component of quantum mechanics, which is likened to Newton's equations in classical mechanics. The equation is presented in its simplest form, and its purpose in describing the wave-like properties of particles, such as electrons, is explained. The paragraph discusses the challenges of solving the equation due to the three-dimensional and dynamic nature of electron behavior in atoms. It also touches on the historical context of the development of quantum mechanics and the Schrodinger equation's role in understanding the stability of the hydrogen atom.

This section of the script highlights ongoing research in quantum mechanics, focusing on the work of Professor Heather Kulik, who is developing computational methods to analyze large systems like proteins using quantum mechanics. The importance of such research is underscored by its potential applications in solving energy problems and understanding materials for new batteries and electrodes. The script also mentions the upcoming demonstration of the hydrogen atom spectrum to illustrate the predictive power of the Schrodinger equation in explaining binding energies.

The final paragraph of the script invites students to an upcoming demonstration and clicker competition, which will further explore the concepts of quantum mechanics and the Schrodinger equation. It encourages students to participate actively, use their clickers during the competition, and collaborate in recitations to enhance their understanding of the material. The script concludes with a reminder of the next class session and an emphasis on the importance of student involvement.