Matter as a Particle

Bozeman Science

8 Jul 201503:52

EducationalLearning

32 Likes 10 Comments

TLDRIn this AP Physics essentials video, Mr. Andersen explains the concept of matter as a particle and its wave-particle duality. He discusses Einstein's work on the photoelectric effect, which demonstrated that photons are both waves and particles, and Louis de Broglie's hypothesis that matter is also composed of waves. De Broglie's formula, which relates the wavelength of matter to Planck's constant and momentum, is highlighted. The video emphasizes that while larger objects like a baseball exhibit negligible wave properties due to their small de Broglie wavelengths, smaller particles such as electrons do exhibit wave-like behavior. The scale of the object determines whether classical mechanics or quantum mechanics is applicable. The video concludes by encouraging viewers to understand the importance of scale in predicting whether matter will behave as a particle or a wave, and hints at applying de Broglie's wavelength to smaller particles in the next video.

Takeaways

🌌 Einstein's photoelectric effect demonstrated that photons have particle characteristics and he calculated their energy.
🌟 Louis de Broglie proposed that matter could also exhibit wave-like properties, which was initially met with skepticism but later earned him a Nobel Prize.
🔍 De Broglie's formula for wavelength relates it to Planck's constant divided by an object's momentum (mass times velocity).
📏 The de Broglie wavelength is typically very small for macroscopic objects, making wave-like behavior undetectable at our scale.
🌊 Matter exhibits wave-particle duality, behaving as both a particle and a wave, similar to light.
🔧 Classical mechanics applies when dealing with matter as a particle, while quantum mechanics is used for wave-like behavior.
🔬 The scale at which we observe matter determines whether classical or quantum mechanics is appropriate.
🏞 Macroscopic and microscopic objects are typically analyzed using classical mechanics.
🌌 Nanoscopic particles exhibit wave-like properties and are better described by quantum mechanics.
📉 De Broglie's wavelength formula helps predict the extent of wave-like effects for different sizes of matter.
🏀 An example calculation with a baseball shows that its de Broglie wavelength is incredibly small, rendering wave effects negligible in classical physics.

Q & A

What was Einstein's contribution to the understanding of photons?
-Einstein demonstrated that photons are not only waves but also particles, using the photoelectric effect, and he calculated the energy of photons.
Who proposed the idea that matter might be made up of waves?
-Louis de Broglie proposed the idea that matter could be made up of waves.
What is the formula that Louis de Broglie came up with to describe the wavelength of matter?
-De Broglie's formula states that the wavelength of matter is equal to Planck’s Constant divided by the momentum (mass times velocity).
Why did de Broglie's mentors send his paper to Einstein?
-De Broglie's mentors were unsure about his thesis, so they sent it to Einstein for his opinion, which was supportive and significant for de Broglie's future Nobel Prize.
How does the de Broglie wavelength formula explain why we do not see matter as waves?
-The formula shows that for objects with large mass compared to Planck’s Constant, the resulting wavelength is incredibly small, making the wave-like behavior of matter undetectable.
What is the term for the dual nature of matter being both a particle and a wave?
-The dual nature of matter is referred to as wave-particle duality.
What determines whether we use classical mechanics or quantum mechanics when dealing with matter?
-The scale or size of the matter determines the model used; macroscopic or microscopic objects are treated with classical mechanics, while nanoscopic particles are treated with quantum mechanics.
What is the mass of a baseball according to the script?
-The mass of a baseball is given as 0.15 kilograms.
What is the velocity of the baseball thrown in the script?
-The velocity of the thrown baseball is 20.0 meters per second.
What is the de Broglie wavelength for a baseball with the given mass and velocity?
-The de Broglie wavelength for the baseball is 2.2 times 10 to the negative thirty-four meters.
How does the size of an object affect the relevance of its de Broglie wavelength in classical physics?
-For larger objects, the de Broglie wavelength is so small that it can be ignored in classical physics. The wavelength becomes significant only for very small particles.
What will be the focus of the next video according to the script?
-The next video will focus on applying de Broglie’s wavelength to smaller matter where the wavelength becomes important.

Outlines

00:00

🌌 Wave-Particle Duality of Matter

In this video, Mr. Andersen introduces the concept of matter as a particle, building upon Einstein's demonstration that photons exhibit both wave and particle characteristics. He discusses Louis de Broglie's hypothesis that matter is also composed of waves, which was validated by a formula relating wavelength to Planck’s Constant and momentum. The video explains that the wave nature of matter is not observable at larger scales due to the smallness of the associated wavelengths, but becomes significant at the nanoscopic level. The de Broglie wavelength formula is used to illustrate how the scale of observation determines whether classical mechanics or quantum mechanics is applicable. The video concludes with an example of calculating the de Broglie wavelength of a baseball, showing that it is so minuscule that it has no practical impact on classical physics.

Mindmap

Keywords

💡Photon

A photon is a particle representing a quantum of light or other electromagnetic radiation. In the video, Einstein's work on the photoelectric effect demonstrated that photons exhibit both wave-like and particle-like properties, leading to the concept of wave-particle duality.

💡Louis de Broglie

Louis de Broglie was a scientist who proposed that matter has wave-like properties. Despite not having his PhD at the time, his thesis suggested that matter's wavelength is equal to Planck’s Constant divided by its momentum, an idea that eventually earned him a Nobel Prize. His work is central to understanding the wave-particle duality of matter.

💡Planck’s Constant

Planck’s Constant is a fundamental constant used in quantum mechanics, denoted as h, which relates the energy of a photon to its frequency. In de Broglie's formula, it is used to calculate the wavelength of matter by dividing it by the momentum of the object.

💡Momentum

Momentum is the product of an object's mass and its velocity. In the context of the video, momentum is used in de Broglie's formula to calculate the wavelength of matter. For example, the momentum of a baseball is calculated to demonstrate why we don't observe wave-like properties in macroscopic objects.

💡Wave-Particle Duality

Wave-Particle Duality is the concept that all particles exhibit both wave and particle properties. The video explains how light and matter exhibit this duality, with classical mechanics describing particle behavior and quantum mechanics describing wave behavior, depending on the scale.

💡Classical Mechanics

Classical Mechanics is the branch of physics that deals with the motion of bodies under the influence of forces, primarily at macroscopic scales. In the video, it is used to describe the behavior of matter when it acts like a particle, as opposed to the wave behavior described by quantum mechanics.

💡Quantum Mechanics

Quantum Mechanics is the branch of physics that deals with the behavior of particles at nanoscopic scales. The video contrasts this with classical mechanics, explaining that matter exhibits wave properties at very small scales, as predicted by de Broglie’s wavelength formula.

💡Relativity

Relativity refers to the theory proposed by Albert Einstein, which describes the behavior of objects at high velocities. The video mentions relativity to illustrate how the scale (speed and size) determines whether classical mechanics, quantum mechanics, or relativistic mechanics are applicable.

💡de Broglie Wavelength

The de Broglie Wavelength is a concept that assigns a wavelength to matter, calculated as Planck’s Constant divided by the momentum. The video uses the example of a baseball to show that for large objects, this wavelength is extremely small, making wave properties negligible at macroscopic scales.

💡Macroscopic

Macroscopic refers to objects and phenomena that are large enough to be seen with the naked eye. In the video, it is explained that at this scale, matter behaves according to classical mechanics, and wave-like properties are not observable.

💡Nanoscopic

Nanoscopic refers to objects and phenomena at a scale of nanometers, where quantum mechanical effects become significant. The video explains that at this tiny scale, matter exhibits wave-like properties, as described by de Broglie’s wavelength.

Highlights

Einstein demonstrated that photons have particle properties using the photoelectric effect.

Louis de Broglie proposed that matter may be composed of waves, contrary to the prevailing scientific view.

De Broglie formulated a relationship between wavelength and momentum using Planck's Constant.

Einstein supported de Broglie's hypothesis, which later won him the Nobel Prize.

The de Broglie wavelength formula explains why we don't perceive everyday matter as waves.

The size of an object's mass relative to Planck's Constant determines its wave-like behavior.

Matter exhibits wave-particle duality, similar to light.

Classical mechanics is used for macroscopic objects, while quantum mechanics applies to nanoscopic particles.

De Broglie's wavelength helps to determine the scale at which wave properties become significant.

We live primarily in a world governed by classical physics due to our size.

Increasing speed brings us into the realm of relativity, while decreasing size leads to quantum mechanics.

The scale of an object dictates whether classical or quantum mechanics should be applied.

An example calculation using de Broglie's wavelength for a baseball shows an extremely small wavelength.

The de Broglie wavelength of a baseball is minuscule compared to the diameter of a hydrogen atom.

In classical physics, the wave properties of matter can often be ignored due to their small scale.

Upcoming videos will apply de Broglie's wavelength to smaller particles where wave properties become important.

The video aims to teach viewers to predict whether to use classical mechanics or quantum mechanics based on scale.

Transcripts

Browse More Related Video

Matter as a Wave

Are Photons & Electrons Particles or Waves? Make up your mind god!

Quantum Mechanics - Part 2: Crash Course Physics #44

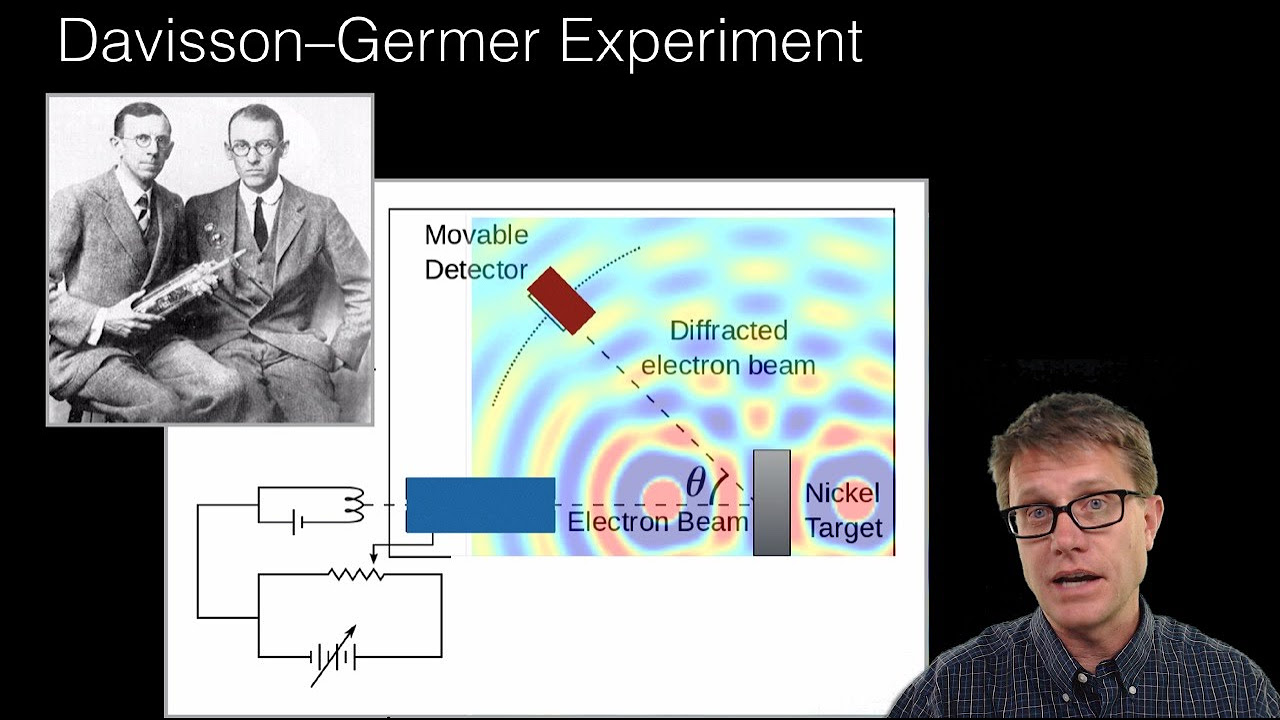
AT&T Archives: Matter Waves, Holden and Germer on Wave Nature and the Davisson-Germer Experiment

Wave-Particle Duality - Part 2

4. Wave-Particle Duality of Matter; Schrödinger Equation

Matter as a Particle

Takeaways

Q & A

What was Einstein's contribution to the understanding of photons?

Who proposed the idea that matter might be made up of waves?

What is the formula that Louis de Broglie came up with to describe the wavelength of matter?

Why did de Broglie's mentors send his paper to Einstein?

How does the de Broglie wavelength formula explain why we do not see matter as waves?

What is the term for the dual nature of matter being both a particle and a wave?

What determines whether we use classical mechanics or quantum mechanics when dealing with matter?

What is the mass of a baseball according to the script?

What is the velocity of the baseball thrown in the script?

What is the de Broglie wavelength for a baseball with the given mass and velocity?

How does the size of an object affect the relevance of its de Broglie wavelength in classical physics?

What will be the focus of the next video according to the script?